Chapter 12 Experience Rating using Bonus-Malus

---

Chapter Preview. This chapter introduces bonus-malus system used in motor insurance ratemaking. In particular, the chapter discusses the features of bonus-malus system and studies its modelling and properties via basic statistical techniques. Section 12.1 introduces the use of bonus-malus system as an experience rating scheme, followed by Section 12.2 which describes its practical implementation in several countries. Section 12.3 covers its modelling setup by a discrete time Markov Chain. Next, Section 12.4 studies a number of simple relevant properties associated with the stationary distribution of bonus-malus system. Section 12.5 focuses on the determination of a posteriori premium rating to complement a priori ratemaking.

---

12.1 Introduction

Bonus-malus systemA type of rating mechanism where insured premiums are adjusted based on their individual loss experience history, which is used interchangeably as “no-fault discount”, “merit rating”, “experience rating” or “no-claim discount” in different countries, is based on penalizing insureds who are responsible for one or more claims by a premium surcharge (malus), and rewarding insureds with a premium discount (bonus) if they do not have any claims. A bonus-malus system can be perceived as a commercial implementation of the ideal credibility premium as discussed in Chapter 9, where premium payable for insureds are calculated on an individual basis. Insurers use bonus-malus systems for two main purposes: to encourage drivers to drive more carefully in a year without any claims, and to ensure insureds to pay premiums proportional to their risks based on their claims experience via an experience rating mechanism.

No Claim Discount (NCD) systemA type of experience rating where insureds obtain discounts on future years’ premiums based on claims-free experience is an experience rating system commonly used in motor insurance. It represents an attempt to categorize insureds into homogeneous groups who pay premiums based on their claims experience. Depending on the rules in the scheme, new policyholders may be required to pay full premium initially, and obtain discounts in the future years as a result of claim-free years. An NCD system rewards policyholders for not making any claims during a year. In other words, it grants a bonus to a careful driver. This bonus principle may affect policy holders’ decisions whether to claim or not to claim, especially when involving accidents with slight damages, which is known as the ‘hunger for bonusPhenomenon where insureds under an experience rating system are dissuaded from filing minor claims in order to keep their no-claims discount’ phenomenon. The ‘hunger for bonus’ under an NCD system may reduce insurers’ claim costs, and may be able to offset the expected decrease in premium income.

12.2 NCD System in Several Countries

12.2.1 NCD System in Malaysia

Before the liberalization of Motor Tariff on 1st July 2017, the rating of motor insurance in Malaysia was governed by the Motor Tariff. Under the tariff, the rate charged should not be lower than the rates specified under the classes of risks, to ensure that the price competition among insurers will not go below the country’s economic level. The basic rating factors considered were scope of insurance, cubic capacity of vehicle and estimated value of vehicle (or sum insured, whichever is lower). Under the Motor Tariff, the final premium to be paid is adjusted by the policyholder’s claim experience, or equivalently, his NCD entitlement.

Effective on 1st July 2017, the premium rates for motor insurance are liberalized, or de-tariffed. The pricing of premium is now determined by individual insurers and takafulCo-operative system of reimbursement or repayment in case of loss as an insurance alternative operators, and the consumers are able to enjoy a wider choice of motor insurance products at competitive prices. Since tariff liberalization encourages innovation and competition among insurers and takaful operators, the premiums are based on broader risk factors other than the two rating factors specified in the Motor Tariff, i.e. sum insured and cubic capacity of vehicle. Other rating factors may be defined in the risk profile of an insured, such as age of vehicle, age of driver, safety and security features of vehicle, geographical location of vehicle and traffic offences of driver. As different insurers and takaful operators have different ways of defining the risk profile of an insured, the price of a policy may differ from one insurer to another. However, the NCD structure from the Motor Tariff remains ‘unchanged’ and continue to exist, and is ‘transferable’ from one insurer, or from one takaful operator, to another.

The discounts in the Malaysian NCD system are divided into six classes, starting from the initial class of 0% discount, followed by classes of 25%, 30%, 38.3%, 45% and 55% discounts. Figure 12.1 provides the classes of NCD system in Malaysia. A claim-free year indicates that a policyholder is entitled to move one-step forward to the next discount class, such as from a 0% discount to a 25% discount in the renewal year. If a policyholder is already at the highest class, which is at a 55% discount, a claim-free year indicates that the policyholder remains in the same class. On the other hand, if one or more claims are made within the year, the NCD will be forfeited and the policyholder has to start at 0% discount in the renewal year. This set of transition rules can also be summarized as a rule of -1/Top, that is, a class of bonus for a claim-free year, and moving to the highest class after having one or more claims. For an illustration purpose, Figure 12.1 shows the classes and the transition diagram for the Malaysian NCD system.

## Warning: package 'gridExtra' was built under R version 3.6.3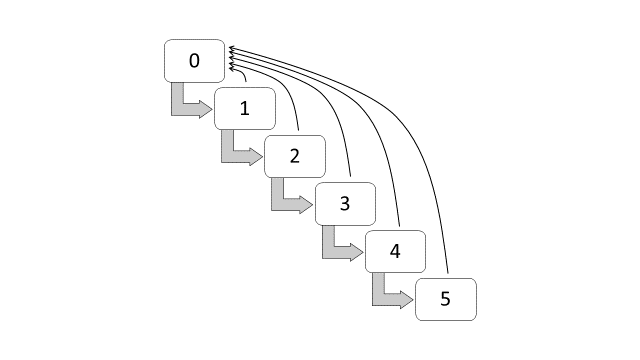

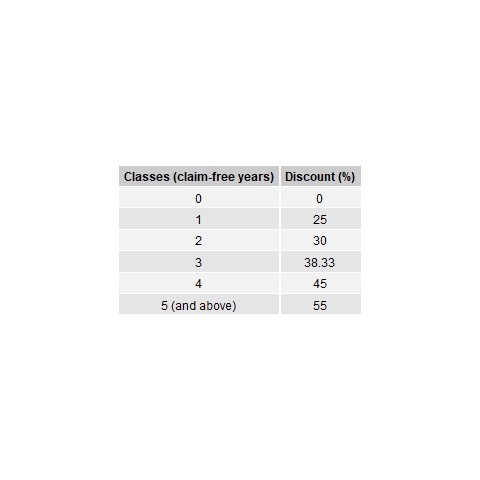
Figure 12.1: Transition Diagram for NCD Classes (Malaysia)

---

12.2.2 NCD Systems in Other Countries

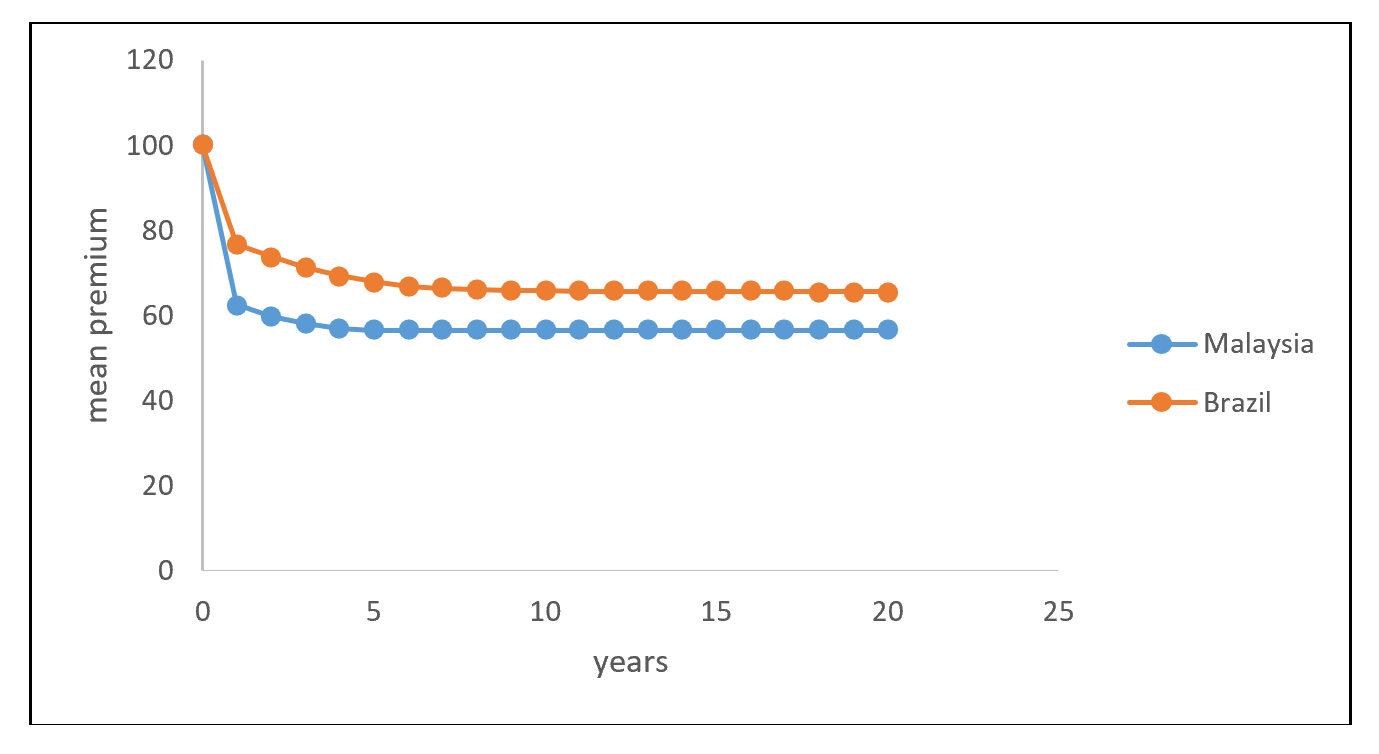
The NCD system in Brazil are subdivided into seven classes, with the following premium levels (Lemaire and Zi 1994): 100, 90, 85, 80, 75, 70, and 65. These premium levels are also equivalent to the following discount classes: 0%, 10%, 15%, 20%, 25%, 30% and 45%. New policyholders have to start at 0% discount, or at premium level of 100, and a claim-free year indicates that a policyholder can move forward at a one-class discount. If one or more claims incurred within the year, the policyholder has to move one-class backward for each claim. Figure 12.2 shows the classes and the transition diagram for the NCD system in Brazil. This set of transition rules can also be summarized as a rule of -1/+1, that is, a class of bonus for a claim-free year, and a class of malus for each claim reported.

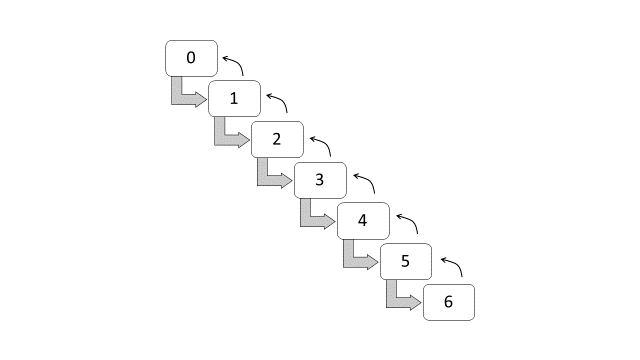
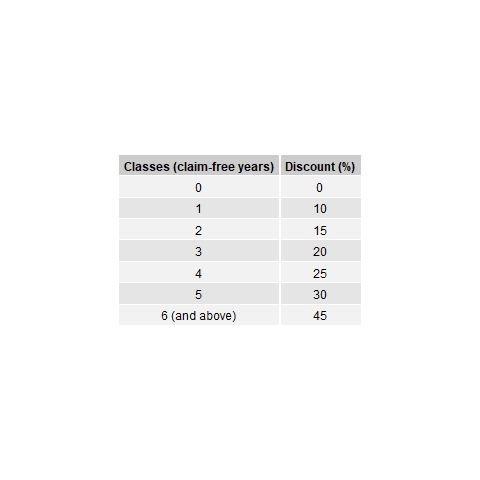
Figure 12.2: Transition Diagram for NCD Classes (Brazil)

---

The NCD system in Switzerland are subdivided into twenty-two classes, with the following premium levels: 270, 250, 230, 215, 200, 185, 170, 155, 140, 130, 120, 110, 100, 90, 80, 75, 70, 65, 60, 55, 50 and 45 (Lemaire and Zi 1994). These levels are also equivalent to the following loadings (malus): 170%, 150%, 130%, 115%, 100%, 85%, 70%, 55%, 40%, 30%, 20%, and 10%, and the following discounts: 0%, 10%, 20%, 25%, 30%, 35%, 40%, 45%, 50% and 55%. New policyholders have to start at 0% discount, or at premium level of 100, and a claim-free year indicates that a policyholder can move one-class forward. If one or more claims incurred within the year, the policyholder has to move four-classes backward for each claim. Table 12.1 and Figure 12.3 respectively show the classes and the transition diagram for the NCD system in Switzerland. This set of transition rule can be summarized as a rule of -1/+4.

Table 12.1. Classes of NCD (Switzerland)

\[ \small{ \begin{array}{*{20}c} \hline \text{Classes} & \text{Loadings } (\%) & \text{Classes} & \text{Discounts } (\%)\\ \hline {0} & {170} & {12} & {0}\\ {1} & {150} & {13} & {10}\\ {2} & {130} & {14} & {20}\\ {3} & {115} & {15} & {25}\\ {4} & {100} & {16} & {30}\\ {5} & {85} & {17} & {35}\\ {6} & {70} & {18} & {40}\\ {7} & {55} & {19} & {45}\\ {8} & {40} & {20} & {50}\\ {9} & {30} & {21} & {55}\\ {10} & {20} && \\ {11} & {10} && \\ \hline \end{array} } \]

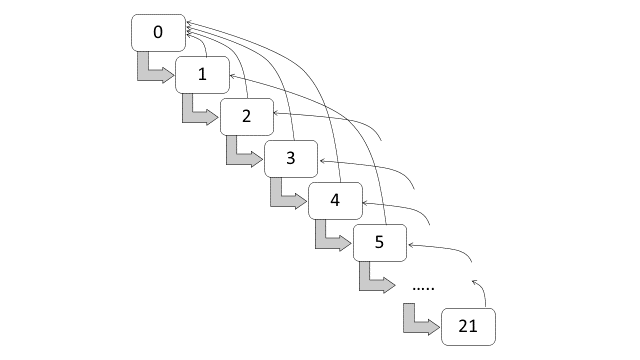
Figure 12.3: Transition Diagram for NCD Classes (Switzerland)

12.3 BMS and Markov Chain Model

A BMS can be represented by a discrete time Markov chainA stochastic model (time dependent) where the probability of each event depends only on the current state and not the historical path. A stochastic process is said to possess the Markov property if the evolution of the process in the future depends only on the present state but not the past. A discrete time Markov Chain is a Markov process with discrete state space.

12.3.1 Transition Probability

A Markov Chain is determined by its transition probabilities. The transition probability from state \(i\) (at time \(n\)) to state \(j\) (at time \(n + 1\)) is called a one-step transition probability, and is denoted by \(p_{ij}(n,n+1) = Pr (X_{n + 1} = j|X_n = i)\), \(i = 1,2,\ldots,k\), \(j = 1,2,\ldots,k\). For general transition from time \(m\) to time \(n\), for \(m<n\), by conditioning on \(X_{o}\) for \(m\le o\le n\), we have the Chapman-Kolmogorov equation of

\[\begin{equation} p_{ij}(m,n)=\sum_{l\in S} p_{il}(m,o)p_{lj}(o,n). \end{equation}\]

A time-homogeneous Markov Chain satisfies the property of \(p_{ij}(n,n+t)=p_{ij}^{(t)}\) for all \(n\). For instance, we have \(p_{ij}(n,n+1)=p_{ij}^{(1)}\equiv p_{ij}\). In this case, the Chapman-Kolmogorov equation can be written as

\[\begin{equation} p_{ij}(0,m+n)=\sum_{l\in S} p_{il}(0,m)p_{lj}(m,m+n)=\sum_{l\in S}p_{il}^{(m)}p_{lj}^{(n)}. \end{equation}\]

In the context of BMS, the transition of the NCD classes is governed by the transition probability in a given year. The transition of the NCD classes is also a time-homogeneous Markov Chain since the set of transition rules is fixed and independent of time. We can represent the one-step transition probabilities by a \(k \times k\) transition matrix \({\bf P}=(p_{ij})\) that corresponds to NCD classes \(0,1,2,\ldots,k-1\).

\[ \small{ {\bf P} = \left[ {\begin{array}{*{20}c} p_{00} & p_{01} & \ldots & & & p_{0k-1} \\ p_{10} & p_{11} & \ldots & & & p_{1k-1} \\ \vdots & \ddots & & & & \vdots \\ p_{k-10} & p_{k-11} & \cdots & & & p_{k-1k-1} \end{array} } \right] } \]

Here, its \((i,j)\)-th element is the transition probability from state \(i\) to state \(j\). In other words, each row of the transition matrixMatrix that represents all probabilities for transition from one state to another (could be same state) for a markov chain represents the transition of flowing out of state, whereas each column represents the transition of flowing into the state. The summation of transition probabilities of flowing out of state must equal to 1, or each row of the matrix must sum to 1, i.e. \(\sum_j p_{ij} = 1\). All probabilities must also be non-negative (since they are probabilities), i.e. \(p_{ij} \ge 0\).

Consider the Malaysian NCD system. Let \(\{X_{t}:t=0,1,2,\ldots\}\) be the NCD class occupied by a policyholder at time \(t\) with state space \(S=\{0,1,2,3,4,5\}\). Therefore, the transition probability in a no-claim year is equal to the probability of transition from state \(i\) to state \(i+1\), i.e. \(p_{ii+1}\). If an insured has one or more claims within the year, the probability of transitioning back to state 0 is represented by \(p_{i0}=1-p_{ii+1}\). Hence, the Malaysian NCD system can be represented by the following \(6\times 6\) transition matrix:

\[ \small{ {\bf P} = \left[ {\begin{array}{*{20}c} p_{00}&p_{01}&0&0&0&0\\ p_{10}&0&p_{12}&0&0&0\\ p_{20}&0&0&p_{23}&0&0\\ p_{30}&0&0&0&p_{34}&0\\ p_{40}&0&0&0&0&p_{45}\\ p_{50}&0&0&0&0&p_{55} \end{array} }\right] = \left[ {\begin{array}{*{20}c} {1 - p_{01}}&p_{01}&0&0&0&0\\ {1 - p_{12}}&0&p_{12}&0&0&0\\ {1 - p_{23}}&0&0&p_{23}&0&0\\ {1 - p_{34}}&0&0&0&p_{34}&0\\ {1 - p_{45}}&0&0&0&0&p_{45}\\ {1 - p_{55}}&0&0&0&0&p_{55} \end{array} }\right] } \]

Example 12.3.1. Provide the transition matrix for the NCD system in Brazil.

Show Example Solution

Solution

Based on the NCD classes and the transition diagram shown in Figure 12.2 , the probability of a no-claim year is equal to the probability of moving one-class forward, whereas the probability of having one or more claims within the year is equal to the probability of moving one-class backward for each claim. Therefore, each row can contain two or more transition probabilities; one probability for advancing to the next state, and one or more probabilities for moving one-class backward. The transition matrix is:

\[ \small{ {\bf P} = \left[ {\begin{array}{*{20}{c}} {1 - p_{01}}&p_{01}&0&0&0&0&0\\ {1 - p_{12}}&0&p_{12}&0&0&0&0\\ {1 - \sum_j p_{2j}}&p_{21}&0&p_{23}&0&0&0\\ {1 - \sum_j p_{3j}}&p_{31}&p_{32}&0&p_{34}&0&0\\\ {1 - \sum_j p_{4j}}&p_{41}&p_{42}&p_{43}&0&p_{45}&0\\ {1 - \sum_j p_{5j}}&p_{51}&p_{52}&p_{53}&p_{54}&0&p_{56}\\ {1 - \sum_j p_{6j}}&p_{61}&p_{62}&p_{63}&p_{64}&p_{65}&p_{66} \end{array} } \right] } \]

---

Example 12.3.2. Provide the transition matrix for the NCD system in Switzerland.

Show Example Solution

Solution.

From Table 12.1 and Figure 12.3, the probability of a no-claim year is equal to the probability of moving one-class forward, whereas the probability of having one or more claims within the year is equal to the probability of moving four-classes backward for each claim. The transition matrix is:

\[ \small{ {\bf P} = \left[ {\begin{array}{*{12}{c}} 1 - {p_{01}} & p_{01} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{12}} & 0 & p_{12} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{23}} & 0 & 0 & p_{23} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{34}} & 0 & 0 & 0 & p_{34} & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{45}} & 0 & 0 & 0 & 0 & p_{45} & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{5j}} & p_{51} & 0 & 0 & 0 & 0 & p_{56} & 0 & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{6j}} & 0 & p_{62} & 0 & 0 & 0 & 0 & p_{67} & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{7j}} & 0 & 0 & p_{73} & 0 & 0 & 0 & 0 & p_{78} & 0 & 0 & \cdots\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots\\ 1 - \sum\limits_j {p_{19,j}} & 0 & 0 & p_{19,3} & 0 & 0 & 0 & p_{19,7} & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{20,j}} & 0 & 0 & 0 & p_{20,4} & 0 & 0 & 0 & p_{20,8} & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{21,j}} & p_{21,1} & 0 & 0 & 0 & p_{21,5} & 0 & 0 & 0 & p_{21,9} & 0 & \cdots \end{array} } \right] } \]

---

12.4 BMS and Stationary Distribution

12.4.1 Stationary Distribution

A stationary distribution of a Markov Chain is a probability distribution that remains unchanged as time progresses into the future. It is represented by a row vector \(\boldsymbol \pi =(\pi_{1},\pi_{2},\ldots,\pi_{k})\) with the following properties:

\[\begin{align} 0\le \pi_{j}\le 1,\notag\\ \sum\limits_{j}\pi_{j}=1,\notag\\ \pi_{j}=\sum\limits_{i}\pi_{i}p_{ij}. \end{align}\]

The last equation can be written as \(\boldsymbol\pi \bf P=\boldsymbol\pi\). The first two conditions are necessary for probability distribution whereas the last property indicates that the row vector \(\boldsymbol\pi\) is invariant (i.e. unchanged) by the one-step transition matrix. In other words, once the Markov Chain has reached the stationary state, its probability distribution will stay stationary over time. Mathematically, the stationary vector \(\boldsymbol\pi\) can also be obtained by finding the left eigenvector of the one-step transition matrix.

Example 12.4.1. Find the stationary distribution for the NCD system in Malaysia assuming that the probability of a no-claim year for all NCD classes are \({p_0}\).

Show Example Solution

Solution. The transition matrix can be re-written as:

\[ \small{ {\bf P} = \left[ {\begin{array}{*{20}c} {1 - p_{0}}&p_{0}&0&0&0&0\\ {1 - p_{0}}&0&p_{0}&0&0&0\\ {1 - p_{0}}&0&0&p_{0}&0&0\\ {1 - p_{0}}&0&0&0&p_{0}&0\\ {1 - p_{0}}&0&0&0&0&p_{0}\\ {1 - p_{0}}&0&0&0&0&p_0 \end{array} }\right] } \]

The stationary distribution can be calculated using \(\pi_{j}=\sum\limits_{i}\pi_{i}p_{ij}\). The solutions are:

\[ \small{ \begin{array}{lll} {\pi _0} = \sum\limits_i {\pi_i}p_{i0} = (1 - {p_0})\sum\limits_i {{\pi _i}} = 1 - {p_0}\\ {\pi _1} = \sum\limits_i {\pi _i}p_{i1} = {\pi_0}{p_{01}} = (1 - {p_0}){p_0}\\ {\pi _2} = \sum\limits_i {\pi _i}p_{i2} = {\pi _1}{p_{12}} = (1 - {p_0}){p_0}^2\\ {\pi _3} = \sum\limits_i {\pi _i}p_{i3} = {\pi _2}{p_{23}} = (1 - {p_0}){p_0}^3\\ {\pi _4} = \sum\limits_i {\pi _i}p_{i4} = {\pi _3}{p_{34}} = (1 - {p_0}){p_0}^4\\ {\pi _5} = \sum\limits_i {\pi _i}p_{i5} = {\pi _4}{p_{45}} + {\pi _5}{p_{55}} = (1 - {p_0}){p_0}^5 + {\pi _5}{p_0}\\ \therefore {\pi _5} = \frac{(1 - {p_0}){p_0}^5}{{(1 - {p_0})}} = {p_0}^5 \end{array} } \]

---

The stationary distribution shown in Example 12.4.1 represents the asymptotic distribution of the NCD system, or the distribution in the long run. As an example, assuming that the probability of a no-claim year is \(p_0 = 0.90,\) the stationary probabilities are:

\[ \small{ \begin{array}{l} {\pi _0} = 1 - {p_0} = 0.1000\\ {\pi _1} = (1 - {p_0}){p_0} = 0.0900\\ {\pi _2} = (1 - {p_0}){p_0}^2 = 0.0810\\ {\pi _3} = (1 - {p_0}){p_0}^3 = 0.0729\\ {\pi _4} = (1 - {p_0}){p_0}^4 = 0.0656\\ {\pi _5} = {p_0}^5 = 0.5905 \end{array} } \]

In other words, \({\pi_0} = 0.10\) indicates that 10% of insureds will eventually belong to class 0, \({\pi _1} = 0.09\) indicates that 9% of insureds will eventually belong to class 1, and so forth, until \({\pi _5} = 0.59\), which indicates that 59% of insureds will eventually belong to class 5.

12.4.2 R Code for a Stationary Distribution

We can use the left eigenvector of a transition matrix to calculate a stationary distribution. The following R code can be used to calculate the left eigenvector:

1. Create a Transition Matrix

#create transition matrix
entries = c(0.1,0.9,0,0,0,0,
            0.1,0,0.9,0,0,0,
            0.1,0,0,0.9,0,0,
            0.1,0,0,0,0.9,0,
            0.1,0,0,0,0,0.9,
            0.1,0,0,0,0,0.9)
(TP <- matrix(entries,nrow=6,byrow=TRUE) )

Show R Output

#create transition matrix
entries = c(0.1,0.9,0,0,0,0,
            0.1,0,0.9,0,0,0,
            0.1,0,0,0.9,0,0,
            0.1,0,0,0,0.9,0,
            0.1,0,0,0,0,0.9,
            0.1,0,0,0,0,0.9)
(TP <- matrix(entries,nrow=6,byrow=TRUE) )

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  0.1  0.9  0.0  0.0  0.0  0.0
[2,]  0.1  0.0  0.9  0.0  0.0  0.0
[3,]  0.1  0.0  0.0  0.9  0.0  0.0
[4,]  0.1  0.0  0.0  0.0  0.9  0.0
[5,]  0.1  0.0  0.0  0.0  0.0  0.9
[6,]  0.1  0.0  0.0  0.0  0.0  0.9

2. Calculate eigenvalues and eigenvectors using the eigen function

#hint -- left eigenvector is the same as right eigenvector of transpose 
#of transition matrix
eigenTP <- eigen(t(TP))
signif(eigenTP$values, digits = 3)
signif(eigenTP$vectors, digits = 3)

Show R Output

#hint -- left eigenvector is the same as right eigenvector of transpose 
#of transition matrix
eigenTP <- eigen(t(TP))
signif(eigenTP$values, digits = 3)

[1]  1.000000+0.000000i -0.000488+0.000355i -0.000488-0.000355i
[4]  0.000187+0.000574i  0.000187-0.000574i  0.000603+0.000000i

signif(eigenTP$vectors, digits = 3)

         [,1]                                  [,2]
[1,] 0.162+0i  0.000000000000115+0.000000000000084i
[2,] 0.145+0i -0.000000000066000-0.000000000203000i
[3,] 0.131+0i -0.000000098000000+0.000000302000000i
[4,] 0.118+0i  0.000384000000000-0.000279000000000i
[5,] 0.106+0i -0.707000000000000+0.000000000000000i
[6,] 0.954+0i  0.707000000000000+0.000000000000000i
                                      [,3]
[1,]  0.000000000000115-0.000000000000084i
[2,] -0.000000000066000+0.000000000203000i
[3,] -0.000000098000000-0.000000302000000i
[4,]  0.000384000000000+0.000279000000000i
[5,] -0.707000000000000+0.000000000000000i
[6,]  0.707000000000000+0.000000000000000i
                                      [,4]
[1,] -0.000000000000044+0.000000000000136i
[2,]  0.000000000172000+0.000000000125000i
[3,]  0.000000257000000-0.000000187000000i
[4,] -0.000147000000000-0.000451000000000i
[5,] -0.707000000000000+0.000000000000000i
[6,]  0.707000000000000+0.000000000000000i
                                      [,5]                  [,6]
[1,] -0.000000000000044-0.000000000000136i  0.000000000000143+0i
[2,]  0.000000000172000-0.000000000125000i  0.000000000213000+0i
[3,]  0.000000257000000+0.000000187000000i  0.000000317000000+0i
[4,] -0.000147000000000+0.000451000000000i  0.000474000000000+0i
[5,] -0.707000000000000+0.000000000000000i  0.707000000000000+0i
[6,]  0.707000000000000+0.000000000000000i -0.707000000000000+0i

3. Calculate the left eigenvector

#divide entry of first column by sum of elements, so that entries sum to 1
#provide answers in 4 decimal places
signif(eigen(t(TP))$vectors[,1]/sum(eigen(t(TP))$vectors[,1]), digits = 4)

Show R Output

#divide entry of first column by sum of elements, so that entries sum to 1
#provide answers in 4 decimal places
signif(eigen(t(TP))$vectors[,1]/sum(eigen(t(TP))$vectors[,1]), digits = 4)

[1] 0.10000+0i 0.09000+0i 0.08100+0i 0.07290+0i 0.06561+0i 0.59050+0i

---

Example 12.4.2. Find the stationary distribution for the NCD system in Brazil assuming that the number of claims is Poisson distributed with parameter \(\lambda = 0.10\).

Show Example Solution

Solution. As given in Appendix Section 18.1, when the number of claims is Poisson distributed with parameter \(\lambda=0.10\), the probability of \(k\) claims is \(p_k = \frac{e^{ - 0.1}{(0.1)}^k}{{k!}},{\rm{ }}k = 0,1,2,\ldots.\)

The transition matrix is:

\[ {\small {\bf{P}} = \left[ {\begin{array}{*{20}{c}} {1 - {p_0}}&{{p_0}}&0&0&0&0&0\\ {1 - {p_0}}&0&{{p_0}}&0&0&0&0\\ {1 -\sum_i {{p_i}} }&{{p_1}}&0&{{p_0}}&0&0&0\\ {1 -\sum_i {{p_i}} }&{{p_2}}&{{p_1}}&0&{{p_0}}&0&0\\ {1 - \sum_i {{p_i}}}&{{p_3}}&{{p_2}}&{{p_1}}&0&{{p_0}}&0\\ {1 - \sum_i{{p_i}} }&{{p_4}}&{{p_3}}&{{p_2}}&{{p_1}}&0&{{p_0}}\\ {1 - \sum_i {{p_i}}}&{{p_5}}&{{p_4}}&{{p_3}}&{{p_2}}&{{p_1}}&{{p_0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.0952}&{0.9048}&0&0&0&0&0\\ {0.0952}&0&{0.9048}&0&0&0&0\\ {0.0047}&{0.0905}&0&{0.9048}&0&0&0\\ {0.0002}&{0.0045}&{0.0905}&0&{0.9048}&0&0\\ {0.0000}&{0.0002}&{0.0045}&{0.0905}&0&{0.9048}&0\\ {0.0000}&{0.0000}&{0.0002}&{0.0045}&{0.0905}&0&{0.9048}\\ {0.0000}&{0.0000}&{0.0000}&{0.0002}&{0.0045}&{0.0905}&{0.9048} \end{array}}\right] } \]

Using the earlier R codes on this transition matrix \({\bf P}\), the stationary probabilities are obtained as:

\[ \left[ {\begin{array}{*{20}{c}} {{\pi _0}}\\ {{\pi_1}}\\ {{\pi _2}}\\ {{\pi _3}}\\ {{\pi _4}}\\ {{\pi_5}}\\ {{\pi _6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.0000}\\ {0.0000}\\ {0.0003}\\ {0.0022}\\ {0.0145}\\ {0.0936}\\ {0.8894} \end{array}} \right] . \]

The probabilities indicate that 89% of insureds will eventually belong to class 6, 9% of insureds will eventually belong to class 5, and 1.5% of insureds will eventually belong to class 4. Other classes would have less than 1% of insureds in the long run.

---

Example 12.4.3. Using the results from Example 12.4.2, find the final premium under the steady state condition assuming that the premium prior to implementing the NCD is \(m\).

Show Example Solution

Solution. Using the stationary probabilities from Example 12.4.2, the stationary final premium is:

\[ \begin{array}{l} = \sum\limits_j \text{(premium)} \times \text{(proportion in class } j \text{ in the long run)} \times \text{(1 - *NCD* in class } j)\\ = m[{\pi _0}(1) + {\pi _1}(1 - 0.9) + {\pi _2}(1 - 0.15) + \ldots + {\pi _6}(1 - 0.35)]\\ = m[0 + 0 + (0.0003)(0.85) + \ldots + (0.8894)(0.65)]\\ = 0.6565m . \end{array} \]

---

The results indicate that the final premium reduce from \(m\) to \(0.6565m\) in the long run under stationary condition if the NCD is considered. From a financial standpoint, this implies that the collected premium is insufficient to cover the expected claim cost of \(m\). This result is not surprising because none of the classes in the NCD system in Brazil impose a malus loading for the policyholders. More importantly, it indicates that NCD will only be financially balanced if there are both bonus and malus classes and the premium levels are re-calculated such that the expected premium under the stationary distribution equals to \(m\).

12.4.3 Premium Evolution

We may be interested to find out the evolution of the mean premium after \(n\) years (or \(n\) steps). Under the NCD system, the n-step transition probability, \(p_{ij}^{(n)}=\Pr(X_{n}=j|X_{0}=i)\), can be used to calculate the evolution of the mean premium. The probability \(p_{ij}^{(n)}\) can be obtained as the \((i,j)\)-th element of the \(n\)-th power of transition matrix \({\bf P}\), that is, \({\bf P}^{n}\).

Example 12.4.4. Observe the premiums in 20 years under the NCD system in Malaysia, assuming that the probability of claims is Poisson distributed with parameter \(\lambda = 0.10\) and the premium prior to implementing the NCD is \(m = 100\).

Show Example Solution

Solution. Under the Malaysian NCD, we use the Poisson probability \(p_k = \frac{e^{ - 0.1}{(0.1)}^k}{k!}\), only for \(k = 0,1\). Therefore, the transition matrix in the first year is:

\[ \small{ {\bf{P}^{(1)}} = \left[{\begin{array}{*{20}{c}} {0.0952}&{0.9048}&0&0&0&0\\ {0.0952}&0&{0.9048}&0&0&0\\ {0.0952}&0&0&{0.9048}&0&0\\ {0.0952}&0&0&0&{0.9048}&0\\ {0.0952}&0&0&0&0&{0.9048}\\ {0.0952}&0&0&0&0&{0.9048} \end{array}} \right] } \]

The premium in the first year, after implementing the NCD, is:

\[ \begin{aligned} &= \sum\limits_j \text{(premium)} \times \text{(average proportion in class } j) \times \text{(1 - *NCD* in class }j) \\ &= m\left[ \frac{\sum\limits_i {p_{i0}}}{6}{(1)} + \frac{\sum\limits_i {p_{i1}}}{6}{(1 - 0.25)} + \ldots + \frac{\sum\limits_i {p_{i5}}}{6}{(1 - 0.55)} \right]\\ &= 100[0.0952(1) + 0.1508(0.75) + \cdots + 0.3016(0.45)]\\ &= 62.55. \end{aligned} \]

Using similar steps, the premium in the \(n\)-th year for \(n = 2,...,20\) can be observed. From R, the premiums in 20 years are:

62.55, 59.87, 58.06, 57.06, 56.58, 56.58, 56.58, 56.58, 56.58, 56.58,

56.58, 56.58, 56.58, 56.58, 56.58, 56.58, 56.58, 56.58, 56.58, 56.58.

---

12.4.4 R Program for Premium Evolution

The following R code can be used to find the premium in the n-th year and the premiums in 20 years under the NCD system in Malaysia (to find the solution in Example 12.4.4).

1. Create a Transition Matrix

#create transition matrix
entries = c(0.0952,0.9048,0,0,0,0,
            0.0952,0,0.9048,0,0,0,
            0.0952,0,0,0.9048,0,0,
            0.0952,0,0,0,0.9048,0,
            0.0952,0,0,0,0,0.9048,
            0.0952,0,0,0,0,0.9048)
(TP <- matrix(entries,nrow=6,byrow=TRUE) )

Show R Output

#create transition matrix
entries = c(0.0952,0.9048,0,0,0,0,
            0.0952,0,0.9048,0,0,0,
            0.0952,0,0,0.9048,0,0,
            0.0952,0,0,0,0.9048,0,
            0.0952,0,0,0,0,0.9048,
            0.0952,0,0,0,0,0.9048)
(TP <- matrix(entries,nrow=6,byrow=TRUE) )

       [,1]   [,2]   [,3]   [,4]   [,5]   [,6]
[1,] 0.0952 0.9048 0.0000 0.0000 0.0000 0.0000
[2,] 0.0952 0.0000 0.9048 0.0000 0.0000 0.0000
[3,] 0.0952 0.0000 0.0000 0.9048 0.0000 0.0000
[4,] 0.0952 0.0000 0.0000 0.0000 0.9048 0.0000
[5,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048
[6,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048

2. Create a function for the \(n\)th power of a square matrix

#create function for nth power of square matrix
powA <- function(n) { 
  if (n==1) return (TP)
  if (n==2) return (TP%*%TP)
  if (n>2) return ( TP%*%powA(n-1))}
#example for n=3
signif(powA(3), digits = 3)

Show R Output

#create function for nth power of square matrix
powA <- function(n) { 
  if (n==1) return (TP)
  if (n==2) return (TP%*%TP)
  if (n>2) return ( TP%*%powA(n-1))}
#example for n=3
signif(powA(3), digits = 3)

       [,1]   [,2]   [,3]  [,4]  [,5]  [,6]
[1,] 0.0952 0.0861 0.0779 0.741 0.000 0.000
[2,] 0.0952 0.0861 0.0779 0.000 0.741 0.000
[3,] 0.0952 0.0861 0.0779 0.000 0.000 0.741
[4,] 0.0952 0.0861 0.0779 0.000 0.000 0.741
[5,] 0.0952 0.0861 0.0779 0.000 0.000 0.741
[6,] 0.0952 0.0861 0.0779 0.000 0.000 0.741

3. create function for premium in nth year

#define NCD percentage
NCD = c(1,.75,.7,.6167,.55,.45)

#create function for premium in nth year
p = numeric(0)
prem <- function(n){
  for (j in 1:length(NCD))
         p[j] = mean(powA(n)[,j])
         100*sum(p*NCD)
         }
#example for n=3
signif(prem(3), digits = 4)

Show R Output

#define NCD percentage
NCD = c(1,.75,.7,.6167,.55,.45)

#create function for premium in nth year
p = numeric(0)
prem <- function(n){
  for (j in 1:length(NCD))
         p[j] = mean(powA(n)[,j])
         100*sum(p*NCD)
         }
#example for n=3
signif(prem(3), digits = 4)

[1] 58.06

4. Provide Premiums for 20 years

premium=numeric(0)
for (n in 1:20) {premium[n] = prem(n) }
signif(premium, digits = 4)

Show R Output

premium=numeric(0)
for (n in 1:20) {premium[n] = prem(n) }
signif(premium, digits = 4)

 [1] 62.55 59.87 58.06 57.06 56.58 56.58 56.58 56.58 56.58 56.58 56.58 56.58
[13] 56.58 56.58 56.58 56.58 56.58 56.58 56.58 56.58

---

Example 12.4.5. Observe the premiums in 20 years under the NCD system in Brazil, assuming that the probability of \(k\) claims is \(p_k = \frac{e^{-0.1}{(0.1)}^k}{k!}, \ \ k = 0,1,2,\ldots\), and the premium prior to implementing the NCD is \(m = 100\).

Show Example Solution

Solution. The transition matrix for the NCD system in Brazil is:

\[ {\bf P} = \left[ {\begin{array}{*{20}{c}} {0.0952}&{0.9048}&0&0&0&0&0\\ {0.0952}&0&{0.9048}&0&0&0&0\\ {0.0047}&{0.0905}&0&{0.9048}&0&0&0\\ {0.0002}&{0.0045}&{0.0905}&0&{0.9048}&0&0\\ {0.0000}&{0.0002}&{0.0045}&{0.0905}&0&{0.9048}&0\\ {0.0000}&{0.0000}&{0.0002}&{0.0045}&{0.0905}&0&{0.9048}\\ {0.0000}&{0.0000}&{0.0000}&{0.0002}&{0.0045}&{0.0905}&{0.9048} \end{array}} \right] \]

Using R, the premiums in 20 years are:

76.69, 73.76, 71.31, 69.38, 67.92, 66.93, 66.40, 66.05, 65.88, 65.78,

65.72, 65.69, 65.67, 65.66, 65.66, 65.66, 65.66, 65.65, 65.65, 65.65.

---

The results in Examples 12.4-5 allow us to observe the evolution of premium for the NCD systems in Malaysia and Brazil assuming that the number of claims is Poisson distributed with parameter \(\lambda = 0.10\), and the premium prior to implementing the NCD is \(m = 100\). The evolution of premiums for both countries are provided in Table 12.4, and are shown graphically in Figure 12.4.

Table 12.4. Evolution of Premium (Malaysia and Brazil)

\[ \small{ \begin{array}{ccc|ccc} \hline \text{Year} & \text{Premium} & \text{Premium} & \text{Year} & \text{Premium} & \text{Premium} \\ & \text{Malaysia} & \text{Brazil} & & \text{Malaysia} & \text{Brazil} \\ \hline 0 & 100 & 100 & 11 & 56.58 & 65.72 \\ 1 & 62.55 & 76.69 & 12 & 56.58 & 65.69 \\ 2 & 59.87 & 73.76 & 13 & 56.58 & 65.67 \\ 3 & 58.06 & 71.31 & 14 & 56.58 & 65.66 \\ 4 & 57.06 & 69.38 & 15 & 56.58 & 65.66 \\ 5 & 56.58 & 67.92 & 16 & 56.58 & 65.66 \\ 6 & 56.58 & 66.93 & 17 & 56.58 & 65.66 \\ 7 & 56.58 & 66.40 & 18 & 56.58 & 65.65 \\ 8 & 56.58 & 66.05 & 19 & 56.58 & 65.65 \\ 9 & 56.58 & 65.88 & 20 & 56.58 & 65.65 \\ \hline \end{array} } \]

Figure 12.4: Evolution of Premium (Malaysia and Brazil)

12.4.5 Convergence Rate

We may also be interested to determine the variation between the probability in the n-th year, \(p_{ij}^{(n)}\), and the stationary probability, \(\pi _j\). The variation between the probabilities can be measured using:

\[ \left| {average(p_{ij}^{(n)}) - {\pi _j}} \right|. \]

Therefore, the total variation can be measured by the sum of variation in all classes:

\[\begin{equation} \sum\limits_j {\left| {average(p_{ij}^{(n)}) - {\pi _j}} \right|}. \end{equation}\]

The total variation is also called the convergence rateAfter n transitions, the sum of variation between the probability in each state vs. the stationary probability because it measures the convergence rate after \(n\) years (or \(n\) transitions). A lower total variation implies a better convergence rate between the \(n\)-step transition probabilities and the stationary distribution.

Example 12.4.6. Provide the total variations (convergence rate) in 20 years under the NCD system in Malaysia, assuming that the probability of claims is Poisson distributed with parameter \(\lambda = 0.10\).

Show Example Solution

Solution. Using R, the stationary probabilities are:

\[ \left[ {\begin{array}{*{20}{c}} {{\pi _0}}\\{{\pi_1}}\\{{\pi _2}}\\ {{\pi _3}}\\{{\pi _4}}\\{{\pi_5}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.0952}\\{0.0861}\\{0.0779}\\ {0.0705}\\{0.0638}\\{0.6064} \end{array}} \right] \]

The transition matrix in the first year is:

\[ {\bf{P}}^{(1)} = \left[ {\begin{array}{*{20}{c}} {0.0952}&{0.9048}&0&0&0&0\\ {0.0952}&0&{0.9048}&0&0&0\\ {0.0952}&0&0&{0.9048}&0&0\\ {0.0952}&0&0&0&{0.9048}&0\\ {0.0952}&0&0&0&0&{0.9048}\\ {0.0952}&0&0&0&0&{0.9048} \end{array}} \right] \]

The variation can be computed as:

\[ \begin{array}{l} \left| {\sum\limits_i {\frac{p_{i0}^{}}{6}} - {\pi _0}} \right| = 0\\ \left|{\sum\limits_i {\frac{p_{i1}^{}}{6}} - {\pi _1}} \right| = 0.0647\\ \vdots \\ \left| {\sum\limits_i \frac{p_{i5}}{6} - {\pi _5}} \right| = .3048 \end{array} \]

Therefore, the total variation in the first year is

\[ \sum\limits_j {\left| {\sum\limits_i {\frac{p_{ij}}{6} - {\pi _j}} } \right|} = 0.6096 . \]

Using R, the total variations (or convergence rate) in 20 years are:

0.6096, 0.3941, 0.2252, 0.0958, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.

---

12.4.6 R Program for Convergence Rate

The following R code can be used to calculate the total variation in the \(n\)th year, and the total variations (convergence rates) in 20 years under the NCD system in Malaysia (the solution in Example 12.4.6).

1. Recall the Transition Matrix

TP

Show R Output

TP

       [,1]   [,2]   [,3]   [,4]   [,5]   [,6]
[1,] 0.0952 0.9048 0.0000 0.0000 0.0000 0.0000
[2,] 0.0952 0.0000 0.9048 0.0000 0.0000 0.0000
[3,] 0.0952 0.0000 0.0000 0.9048 0.0000 0.0000
[4,] 0.0952 0.0000 0.0000 0.0000 0.9048 0.0000
[5,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048
[6,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048

2. Create stationary probabilities

SP <- eigen(t(TP))$vectors[,1]/sum(eigen(t(TP))$vectors[,1])
signif(SP, digits = 3)

Show R Output

SP <- eigen(t(TP))$vectors[,1]/sum(eigen(t(TP))$vectors[,1])
signif(SP, digits = 3)

[1] 0.0952+0i 0.0861+0i 0.0779+0i 0.0705+0i 0.0638+0i 0.6060+0i

3. Create a function for total variation in \(n\)th year

TV=function(n){
  dif  =numeric(0)
  for (j in 1:length(SP))
  dif[j]=abs(mean(powA(n)[,j])-SP[j])
  sum(dif)
  }
#example for n=1
signif(TV(1), digits = 4)

Show R Output

TV=function(n){
  dif  =numeric(0)
  for (j in 1:length(SP))
  dif[j]=abs(mean(powA(n)[,j])-SP[j])
  sum(dif)
  }
#example for n=1
signif(TV(1), digits = 4)

[1] 0.6096

4. Provide total variations (convergence rate) in 20 years

tot.var=numeric(0)
for (n in 1:20) {tot.var[n] = TV(n)}
signif(tot.var,4)

Show R Output

tot.var=numeric(0)
for (n in 1:20) {tot.var[n] = TV(n)}
signif(tot.var,4)

 [1] 6.096e-01 3.941e-01 2.252e-01 9.580e-02 4.177e-15 4.274e-15 4.372e-15
 [8] 4.483e-15 4.594e-15 4.594e-15 4.594e-15 4.594e-15 4.594e-15 4.594e-15
[15] 4.594e-15 4.594e-15 4.594e-15 4.594e-15 4.594e-15 4.594e-15

Example 12.4.7. Provide the total variations (or convergence rate) in 20 years under the NCD system in Brazil, assuming that the number of claims is distributed as Poisson with parameter \(\lambda = 0.10\).

Show Example Solution

Solution. Using R code, the total variations (or convergence rates) in 20 years for the NCD system in Brazil are:

1.2617, 1.0536, 0.8465, 0.6412, 0.4362, 0.2316, 0.1531, 0.0747, 0.0480, 0.0232,

0.0145, 0.0071, 0.0043, 0.0021, 0.0013, 0.0006, 0.0004, 0.0002, 0.0001, 0.0001.

---

Examples 12.4.6-7 provide the degree of convergence for two different BMS (two different countries). The Malaysian BMS reaches full stationary only after five years, while the BMS in Brazil takes a longer period. As mentioned in Lemaire (1998), a more sophisticated BMS would converge more slowly, and is considered as a drawback as it takes a longer period to stabilize. The main objective of a BMS is to separate the good drivers from the bad drivers, and thus, it is desirable to have a classification process that can be finalized (or stabilized) as soon as possible.

12.5 BMS and Premium Rating

12.5.1 Premium Rating

In motor insurance ratemaking, BMS is a form of a posteriori rating mechanism to complement the use of a priori risk classification as described in Chapter 8. The a priori risk segmentation introduced in Section 8.1 divides portfolio of drivers into a number of homogeneous risk classes based on observable rating factors (see Section 7.4.2), such that policyholders in the same risk class pay the same a priori premium. The underlying reason for utilizing BMS that relies on claims experience information is to deal with the residual heterogeneity within each homogeneous risk class (e.g., see the discussion before Example 2.6.2) since the observable variables are far from perfect in predicting the riskiness of driving behaviors.

The ideal a posteriori mechanism is the credibility premium framework developed in Chapter 9 and in particular Section 9.5 (see also Dionne and Vanasse (1989)), whereby premiums are derived on an individual basis for each policyholder by incorporating both the a priori and a posteriori information. However, such individual premium determination is overly complex from a commercial standpoint for practical implementations by motor insurers. For this reason, BMS is the preferred solution and it consists of the following three building blocks: (a) BMS classes; (b) transition rules; (c) premium levels (also known as premium relativities or premium adjustment coefficients).

The first two building blocks are pre-specified in advance and have been discussed in previous sections, whereas the determination (instead of pre-determined as discussed in the cases of Malaysian, Brazilian and Swiss systems) of premium relativities are important for motor insurers precisely because of its complementary and correction nature to account for the imperfection or inaccuracies in the a priori risk classification. Note that the premium relativities under BMS are different from the relativity measure defined in Section 7.4.2, which is the ratio between the expected risk of a given risk class to a baseline risk class, both of which are calculated from observable rating factors. In the following subsections, we briefly introduce the required modelling setup to study the determination of optimal relativities. We refer interested reader to Denuit et al. (2007) for a fuller discussion on the technical details.

12.5.2 A Priori Risk Classification

Let us consider a portfolio of \(n\) policies, where the risk exposure (see Section 7.4.1) of driver \(i\) is denoted as \(m_{i}\) and the number of claims reported is represented by \(Y_{i}\), following from the notations used in Section 8.2. Let \({\bf x}_{i}^{T}=(x_{i1},x_{i2},\ldots, x_{iq})\) be the vector of observable variables for \(i=1,2,\ldots, n\). The Poisson regression as developed in Section 8.2 is commonly chosen to model \(Y_{i}\) under the generalized linear models (GLM) framework, see Section 13.3.2.2 and also McCullagh and Nelder (1989).

We can then express the predicted a priori expected claim frequency for policyholder \(i\) as

\[ \mu_{i}=m_{i}\lambda_{i}=m_{i}\exp\left(\hat{\beta}_{0}+\sum\limits_{m=1}^{q}\hat{\beta}_{m}x_{im}\right) , \] where \(\hat{\beta}_{0},\hat{\beta}_{1},\ldots,\hat{\beta}_{q}\) are the estimated regression coefficients. In other words, \(\lambda_{i}=\frac{\mu_{i}}{m_{i}}\) is the expected claim frequency per unit exposure, which is the main focus of the a priori risk classification.

12.5.3 Modelling of Residual Heterogeneity

Since unobserved factors that may affect driving behaviors are not taken into account in estimating the expected claim frequency, insurers would have to account for the residual heterogeneity within each a priori risk class by introducing a random effect component \(\Theta_{i}\) into the conditional distribution of \(Y_{i}\). Given \(\Theta_{i}=\theta\), \(Y_{i}\) follows a Poisson distribution with mean \(\lambda_{i}\theta\), that is,

\[\begin{equation} \Pr(Y_{i}=k|\Theta_{i}=\theta)=\exp(-\lambda_{i}\theta)\frac{(\lambda_{i}\theta)^{k}}{k!},k=0,1,2,\ldots. \end{equation}\]

Following from the setup of gamma-Poisson model in Section 9.5.1, we further assume that all the \(\Theta_{i}\)’s are independent and follow a gamma \((a,a)\) distribution with the following density function as introduced in Appendix 18.2 \[\begin{equation} f(\theta)=\frac{1}{\Gamma(a)}a^{a}\theta^{a-1}\exp(-a\theta), \quad \theta > 0, \end{equation}\] where the use of gamma-Poisson mixture produces a negative binomial distribution for \(Y_{i}\) (see Section 2.6). With these specifications, we obtain \(\mathrm{E}(\Theta_{i})=1\) and hence \(\mathrm{E}(Y_{i})=\mathrm{E}(\mathrm{E}(Y_{i}|\Theta_{i}))=\mathrm{E}(\lambda_{i}\Theta_{i})=\lambda_{i}\). by the law of iterated expectation in Appendix 16.2.1.

Furthermore, it can be shown that the posterior distribution of \(\Theta| y_{1}=k_{1},y_{2}=k_{2},\ldots,y_{n}=k_{n}\) is gamma distributed with parameters \(a+\sum_{j=1}^{n} k_{j}\) and \(a+n\lambda_{i}\) and therefore the Bayesian premium is given as \[\begin{equation} \mathrm{E}(\lambda_{i}\Theta| y_{1}=k_{1},\ldots,y_{n}=k_{n})=\lambda_{i}\times\frac{a+\sum_{j=1}^{n} k_{j}}{a+n\lambda_{i}}. \end{equation}\] On the other hand, applying the Bühlmann credibility-weighted estimate in Section 9.3 to the gamma-Poisson model in Section 9.5.1, we obtain \[\begin{align*} EPV&=\mathrm{E}(\mathrm{Var}(Y| \lambda_{i}))=\mathrm{E}(\lambda_{i}\Theta)=\lambda_{i},\\ VHM&=\mathrm{Var}(\mathrm{E}(Y| \lambda_{i}))=\mathrm{Var}(\lambda_{i}\Theta)=\frac{\lambda_{i}^{2}}{a},\\ K&=\frac{EPV}{VHM}=\frac{\lambda_{i}}{\frac{\lambda_{i}^{2}}{a}}=\frac{a}{\lambda_{i}},\\ Z&=\frac{n}{n+K}=\frac{n\lambda_{i}}{n\lambda_{i}+a},\\ \bar{Y}&=\frac{\sum_{j=1}^{n} y_{j}}{n}=\frac{\sum_{j=1}^{n} k_{j}}{n},\\ \mu&=\mathrm{E}(\mathrm{E}(Y_{i}| \lambda_{i}))=\mathrm{E}(\lambda_{i}\Theta)=\lambda_{i}, \end{align*}\] and hence the credibility-weighted estimate as \[\begin{align} \mathrm{E}(\mathrm{E}(Y| \lambda_{i})| y_{1}=k_{1},\ldots,y_{n}=k_{n})&=\mathrm{E}(\lambda_{i}\Theta| y_{1}=k_{1},\ldots,y_{n}=k_{n})\notag\\ &=Z\times \bar{Y}+ (1-Z)\times \mu\notag\\ &=\frac{n\lambda_{i}}{n\lambda_{i}+a}\times \frac{\sum_{j=1}^{n} k_{j}}{n}+\frac{a}{n\lambda_{i}+a}\times\lambda_{i}\notag\\ &=\frac{\lambda_{i}(a+\sum_{j=1}^{n} k_{j})}{a+n\lambda_{i}}, \end{align}\] that is, the Bühlmann credibility premium exactly matches the Bayesian premium.

Despite the fact that the credibility premium derived on an individual basis above is the ideal a posteriori premium, in practice insurers make use of BMS as a discrete approximation to the Bayesian premium, due to the relatively simpler structure of BMS as compared to the individual calculations of credibility premium.

12.5.4 Stationary Distribution Allowing for Residual Heterogeneity

Suppose that a driver is selected at random from the portfolio that has been classified into \(h\) risk classes via the use of observed a priori variables. The true expected claim frequency for this driver is given by \(\Lambda\Theta\), where \(\Lambda\) is the unknown a priori expected claim frequency and \(\Theta\) is the random residual heterogeneity. Let us further denote \(w_{g}\) as the proportion of drivers in the \(g\)-th risk class, that is, \(w_{g}=\Pr(\Lambda=\lambda_{g})=\frac{n_{g}}{n}\) where \(n_{g}\) is the number of drivers classified in the \(g\)-th risk class. Note that since there are two different concepts of risk classes (from a priori risk classification) and BMS (or NCD) classes (for a posteriori rating mechanism), for the rest of this chapter we will refer BMS classes as BMS levels instead to avoid unnecessary confusion.

Let \(p_{ij}^{\lambda}(\lambda\theta)\) be the transition probability of moving from BMS level \(i\) to level \(j\) for a driver with expected claim frequency \(\lambda\theta\) belonging to the risk class with predicted claim frequency of \(\lambda\). In other words, the one-step transition matrix can be written as \({\bf P}(\lambda\theta; \lambda)=\{p_{ij}^{\lambda}(\lambda\theta)\}\). The row vector of the stationary distribution \(\boldsymbol \pi=(\pi_{0}^{\lambda}(\lambda\theta),\pi_{1}^{\lambda}(\lambda\theta),\ldots,\pi_{k-1}^{\lambda}(\lambda\theta))\) can be obtained by solving the following conditions: \[\begin{align*} \boldsymbol\pi(\lambda\theta;\lambda)&=\boldsymbol\pi(\lambda\theta;\lambda){\bf P}(\lambda\theta;\lambda)\\ \boldsymbol\pi(\lambda\theta;\lambda){\bf 1}&=1, \end{align*}\] where \(\bf 1\) is the column vector of \(1\)’s and \(\pi_{\ell}^{\lambda}(\lambda\theta)\) is the stationary probability for a driver with true expected claim frequency of \(\lambda\theta\) to be in level \(\ell\) when the equilibrium steady state is reached in the long run. Note that with the incorporation of random effect parameter \(\theta\), the expression (not numerical values) for \(\pi_{\ell}^{\lambda}(\lambda\theta)\) can be found by say MATLAB but not R.

With these setup, the probability of drivers staying in BMS level \(L=\ell\) for \(\ell=0,1,\ldots,k-1\) in the context of the entire portfolio can be obtained as \[\begin{align} \Pr(L=\ell)&=\sum\limits_{g=1}^{h}\Pr(L=\ell|\Lambda=\lambda_{g})\Pr(\Lambda=\lambda_{g})\notag\\ &=\sum\limits_{g=1}^{h}\Pr(\Lambda=\lambda_{g})\int_{0}^{\infty}\Pr(L=\ell|\Lambda=\lambda_{g},\Theta=\theta)f(\theta)d\theta\notag\\ &=\sum\limits_{g=1}^{h}w_{g}\int_{0}^{\infty}\pi_{\ell}^{\lambda_{g}}(\lambda_{g}\theta)f(\theta)d\theta. \end{align}\]

12.5.5 Determination of Optimal Relativities

The optimal relativity for each BMS level was first derived by Norberg (1976) through the minimization of the following objective function, which is more commonly known as the Norberg’s criterion: \[\begin{equation*} \min \mathrm{E}\left((\bar{\lambda}\Theta-\bar{\lambda}r_{L})^{2}\right)\equiv\min\mathrm{E}\left((\Theta-r_{L})^{2}\right), \end{equation*}\] where \(\hat{\lambda}\) is the constant expected claim frequency for all policyholders in the absence of a priori risk classification and \(r_{L}\) is the premium relativity for BMS level \(L\). Pitrebois, Denuit, and Walhin (2003) then incorporated the information of a priori risk classification into the optimization of the same objective function of \[\begin{equation*} \min\mathrm{E}\left((\Theta-r_{L})^{2}\right) \end{equation*}\] to derive \(r_{L}\) analytically. Tan et al. (2015) further proposed the minimization of the following objective function \[\begin{equation} \min\mathrm{E}\left((\Lambda\Theta-\Lambda r_{L})^{2}\right), \text{ subject to } \mathrm{E}(r_{L})=1, \end{equation}\] under a financial balanced constraint (that is, the expected premium relativity equals 1) to determine the optimal relativities of a BMS given pre-specified BMS levels and transition rules, where \[\begin{align*} \min\mathrm{E}\left((\Lambda\Theta-\Lambda r_{L})^{2}\right)&=\sum\limits_{\ell=0}^{k-1}\mathrm{E}\left((\Lambda\Theta-\Lambda r_{L})^{2}|L=\ell\right)\Pr(L=\ell)\\ &=\sum\limits_{\ell=0}^{k-1}\mathrm{E}\left(\mathrm{E}\left((\Lambda\Theta-\Lambda r_{L})^{2}|L=\ell,\Lambda\right)|L=\ell\right)\Pr(L=\ell)\\ &=\sum\limits_{\ell=0}^{k-1}\sum\limits_{g=1}^{h}\mathrm{E}\left((\Lambda\Theta-\Lambda r_{L})^{2}|L=\ell,\Lambda=\lambda_{g}\right)\times\Pr\left(\Lambda=\lambda_{g}|L=\ell\right)\Pr(L=\ell)\\ &=\sum\limits_{\ell=0}^{k-1}\sum\limits_{g=1}^{h}\int_{0}^{\infty}(\lambda_{g}\theta-\lambda_{g}r_{\ell})^{2}\pi_{\ell}(\lambda_{g}\theta)w_{g}f(\theta)d\theta\\ &=\sum\limits_{g=1}^{h}w_{g}\int_{0}^{\infty}\sum\limits_{\ell=0}^{k-1}(\lambda_{g}\theta-\lambda_{g}r_{\ell})^{2}\pi_{\ell}(\lambda_{g}\theta)f(\theta)d\theta. \end{align*}\] It is crucially important that the optimal relativity has an average of 100%, so that the bonuses and maluses exactly offset each other to result in a financial equilibrium condition. Note that the approach considered by Pitrebois, Denuit, and Walhin (2003) does not require the financial balanced constraint because the analytical solution to its objective function is given by \(r_{\ell}=\mathrm{E}(\Theta|L=\ell)\), so it follows that \(\mathrm{E}(r_{L})=\mathrm{E}\left(\mathrm{E}(\Theta|L)\right)=\mathrm{E}(\Theta)=1\) with the specific choice of gamma \((a,a)\) distribution for the random effect component \(\Theta\).

In this case, the optimization problem can be solved by specifying the Lagrangian as \[\begin{align} \mathcal{L}({\bf r}, \alpha)&=\mathrm{E}\left((\Lambda\Theta-\Lambda r_{L})^{2}\right)+\alpha(\mathrm{E}(r_{L})-1)\notag\\ &=\sum\limits_{\ell=0}^{k-1} \mathrm{E}\left((\Lambda\Theta-\Lambda r_{L})^{2}|L=\ell\right)\Pr(L=\ell)+\alpha\left(\sum\limits_{\ell=0}^{k-1}r_{\ell}\Pr(L=\ell)-1\right),\notag \end{align}\] where \({\bf r}=(r_{0},r_{1},\ldots,r_{k-1})^{T}\). The required first order conditions are given as follows \[\begin{align*} \Pr(L=\ell)\times \left(2\mathrm{E}\left(\Lambda^{2}\Theta-\Lambda^{2}r_{L}|L=\ell\right)-\alpha\right)&=0, \qquad \ell=0,1,\ldots, k-1,\\ \sum\limits_{\ell=0}^{k-1}r_{\ell}\Pr(L=\ell)-1&=0. \end{align*}\] Finally, the solution set for \(\alpha\) and \(r_{\ell}, \ell=0,1,\ldots,k-1\) is obtained as \[\begin{align*} \alpha&=\frac{\left(\sum\limits_{\ell=0}^{k-1}\frac{\mathrm{E}(\Lambda^{2}\Theta|L=\ell)\Pr(L=\ell)}{\mathrm{E}(\Lambda^{2}|L=\ell)}\right)-1}{\sum\limits_{\ell=0}^{k-1}\frac{\Pr(L=\ell)}{2\mathrm{E}(\Lambda^{2}|L=\ell)}},\\ r_{\ell}&=\frac{\mathrm{E}(\Lambda^{2}\Theta|L=\ell)}{\mathrm{E}(\Lambda^{2}|L=\ell)}-\frac{\alpha}{2\mathrm{E}(\Lambda^{2}|L=\ell)}, \end{align*}\] where \[\begin{align*} \Pr(L=\ell)&=\sum\limits_{g=1}^{h}w_{g}\int_{0}^{\infty}\pi_{\ell}^{\lambda_{g}}(\lambda_{g}\theta)f(\theta)d\theta,\\ \mathrm{E}(\Lambda^{2}\Theta|L=\ell)&=\frac{\sum\limits_{g=1}^{h}w_{g}\int_{0}^{\infty}\lambda_{g}^{2}\theta\pi_{\ell}^{\lambda_{g}}(\lambda_{g}\theta)f(\theta)d\theta}{\sum\limits_{g=1}^{h}w_{g}\int_{0}^{\infty}\pi_{\ell}^{\lambda_{g}}(\lambda_{g}\theta)f(\theta)d\theta},\\ \mathrm{E}(\Lambda^{2}|L=\ell)&=\frac{\sum\limits_{g=1}^{h}w_{g}\int_{0}^{\infty}\lambda_{g}^{2}\pi_{\ell}^{\lambda_{g}}(\lambda_{g}\theta)f(\theta)d\theta}{\sum\limits_{g=1}^{h}w_{g}\int_{0}^{\infty}\pi_{\ell}^{\lambda_{g}}(\lambda_{g}\theta)f(\theta)d\theta}. \end{align*}\] If we perform the optimization without the financial balanced constraint, then we obtain \[\begin{align*} \alpha^{\text{unconstrained}}&=0,\\ r_{\ell}^{\text{unconstrained}}&=\frac{\mathrm{E}(\Lambda^{2}\Theta|L=\ell)}{\mathrm{E}(\Lambda^{2}|L=\ell)}. \end{align*}\]

12.5.6 Numerical Illustrations

In this section, we present two numerical illustrations that integrate a priori information into the determination of optimal relativities. We consider the BMS levels and the transition rules of both Malaysian and Brazilian systems but choose to calculate the set of optimal relativities instead of the specified premium levels given earlier. In our illustrations, we also assume that the following 3 values of a priori expected claim frequency are given
\(\lambda_{1}=0.1\),\(\lambda_{2}=0.3\), and \(\lambda_{3}=0.5\) with the following proportions

\[ \Pr(\Lambda=\lambda_{1})=0.6, \Pr(\Lambda=\lambda_{2})=0.3, \Pr(\Lambda=\lambda_{3})=0.1. \]

We also assume that the gamma parameter is fixed at \(a=1.5\). Note that while these modelling assumptions are simple, the purpose here is to demonstrate the determination of optimal relativities under a relatively simple setup, and that the optimization procedure for the BMS remains the same even if the a priori risk classification is performed extensively. We refer interested readers to the motor vehicle claims data as documented in De Jong and Heller (2008) to conduct the a priori risk segmentation before proceeding to the determination of optimal relativities.

Furthermore, as mentioned earlier, the inclusion of random effect parameter \(\theta\) implies that the required expression (not numerical values) for stationary probabilities \(\pi_{\ell}^{\lambda}(\lambda\theta)\) to be used for subsequent integrals can be found by say MATLAB but not R. Also, since the obtained form of stationary probabilities are rather complex, in this subsection we choose not to include any R codes for the determination of optimal relativities. More importantly, we hope that the key take-away for this subsection is for readers to get a solid overall conceptual understanding on how to account for all the relevant information in the design of a bonus-malus system.

For the Malaysian BMS with 6 levels and the transition rule of -1/Top, the obtained numerical values of optimal relativities are presented in Table 12.5 together with the stationary probabilities. We find that around half of the policyholders will occupy the highest BMS level with the lowest premium relativity over the long run when the stationary state has been reached. We also observe that the constrained optimal relativities are higher than the unconstrained counterparts because of the need to satisfy the financial balanced constraint.

Table 12.5. Optimal Relativities with \(k=6\) levels and transition rule of -1/Top

\[ \small{ \begin{array}{*{20}c} \hline \text{Level }\ell & \Pr(L=\ell) & r_{\ell} & r_{\ell}^{\text{unconstrained}}\\ \hline {0} & {16.22\%} & {131.99\%} & {126.33\%}\\ {1} & {11.29\%} & {127.33\%} & {120.66\%}\\ {2} & {8.49\%} & {120.64\%} & {113.03\%}\\ {3} & {6.69\%} & {113.93\%} & {105.44\%}\\ {4} & {5.44\%} & {107.79\%} & {98.47\%}\\ {5} & {51.87\%} & {78.06\%} & {63.15\%}\\ {E(r_{L})} & & {100\%} & {88.87\%} \\ \hline \end{array} } \]

Moreover, we see that except for the highest BMS level (level 5), other BMS levels will impose malus surcharges to policyholders occupying those levels. This finding is not surprising since our theoretical framework here is to determine optimal relativities given the calculation of a priori base premiums by solely relying on claim frequency information but not claim severity. In practice, insurers could afford to introduce NCD levels with only discounts (bonuses) but not loadings (maluses) because the a priori base premiums have been inflated accordingly taking into account both the information of claim frequency and claim severity.

For the Brazilian BMS with 7 levels and the transition rule of -1/+1, the corresponding numerical values of optimal relativities are shown in Table 12.6. We find that around three quarters of the policyholders will occupy the highest BMS level with the lowest premium relativity in the stationary state. This finding is mainly due to the less severe penalty in the transition rule of -1/+1 in comparison to the rule of -1/Top, so more policyholders are expected to occupy the highest BMS level. Similar to the earlier example, we find that the unconstrained optimal relativities are lower and result in a lower value of \(\mathrm{E}(r_{L})\).

Table 12.6. Optimal Relativities with \(k=7\) levels and transition rule of -1/+1

\[ \small{ \begin{array}{*{20}c} \hline \text{Level }\ell & \Pr(L=\ell) & r_{\ell} & r_{\ell}^{\text{unconstrained}}\\ \hline {0} & {3.28\%} & {234.94\%} & {228.65\%}\\ {1} & {2.21\%} & {196.24\%} & {189.27\%}\\ {2} & {2.00\%} & {168.36\%} & {160.59\%}\\ {3} & {2.38\%} & {145.96\%} & {137.03\%}\\ {4} & {4.02\%} & {125.53\%} & {114.63\%}\\ {5} & {10.38\%} & {106.25\%} & {91.12\%}\\ {6} & {75.74\%} & {85.89\%} & {61.74\%}\\ {E(r_{L})} & & {100\%} & {78.97\%} \\ \hline \end{array} } \]

Note that the obtained values of optimal relativities may not be desirable for commercial implementations because of the possibility of irregular differences between adjacent BMS levels. To alleviate this problem, insurers could consider imposing linear optimal relativities in the form of \(r_{L}^{\text{linear}}=a+bL\) by solving the following constrained optimization with an inequality constraint

\[ \min\mathrm{E}\left((\Lambda\Theta-\Lambda a-\Lambda bL)^{2}\right) \text{ subject to } a+b\mathrm{E}(L)\ge 1. \]

We refer interested readers to Tan (2016) for a discussion on how to incorporate further commercial constraints and also on the solution to this optimization problem involving Kuhn-Tucker conditions.

12.6 Further Resources and Contributors

12.6.1 Further Reading and References

Note that our discussions in Section 12.5 focus on the classical frequency-driven BMS, which implicitly assume that the information of frequency and severity are independent, consistent with the collective risk model as discussed in Section 5.3. However, a number of recent empirical studies (Edward W. Frees, Lee, and Yang (2016); Garrido, Genest, and Schulz (2016)) point towards the need due to their significant dependence structure. In this regard, Oh, Kim, and Ahn (2020) and Oh, Shi, and Ahn (2020) propose recent BMS framework that allows for such frequency-severity dependence based on the bivariate random effect model, where the former utilize both frequency and severity information in the specification of transition rule.

On the other hand, the framework presented in Section 12.5 is found to suffer from a double-counting problem, which results in biased premiums due to the dual role of the a priori rating factors in affecting both the a priori risk classification as well as a posteriori experience rating. We refer interested readers to Oh et al. (2020) who propose to incorporate the estimation of a priori rate (in addition to the a posteriori rate) under a full optimization process to resolve the double-counting problem.

Contributors

• Noriszura Ismail, Universiti Kebangsaan Malaysia and Chong It Tan, Macquarie University, are the principal authors of the initial version of this chapter. Email: ni@ukm.edu.my or chongit.tan@mq.edu.au for chapter comments and suggested improvements.
• This chapter has not yet been reviewed. Write Noriszura, Chong It, or Jed Frees (jfrees@bus.wisc.edu) if you are interested.

Bibliography

De Jong, Piet, and Gillian Z. Heller. 2008. Generalized Linear Models for Insurance Data. Cambridge University Press, Cambridge.

Denuit, Michel, Xavier Maréchal, Sandra Pitrebois, and Jean-François Walhin. 2007. Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. John Wiley & Sons, Chichester.

Dionne, Georges, and Charles Vanasse. 1989. “A Generalization of Automobile Insurance Rating Models: The Negative Binomial Distribution with a Regression Component.” ASTIN Bulletin 19(2): 199–212.

Frees, Edward W., Gee Lee, and Lu Yang. 2016. “Multivariate Frequency-Severity Regression Models Under Insurance.” Risks 4(1): 4.

Garrido, Jose, Christian Genest, and Juliana Schulz. 2016. “Generalized Linear Models for Dependent Frequency and Severity of Insurance Claims.” Insurance: Mathematics and Economics 70: 205–15.

Lemaire, Jean. 1998. “Bonus-Malus Systems: The European and Asian Approach to Merit Rating.” North American Actuarial Journal 2(1): 26–38.

Lemaire, Jean, and Hongmin Zi. 1994. “A Comparative Analysis of 30 Bonus-Malus Systems.” ASTIN Bulletin 24(2): 287–309.

McCullagh, Peter, and John A. Nelder. 1989. Generalized Linear Models, Second Edition. Chapman and Hall/Crc Monographs on Statistics and Applied Probability Series. Chapman & Hall, London.

Norberg, Ragnar. 1976. “A Credibility Theory for Automobile Bonus System.” Scandinavian Actuarial Journal 2: 92–107.

Oh, Rosy, Joseph H. T. Kim, and Jae Youn Ahn. 2020. “Designing a Bonus-Malus System Reflecting the Claim Size Under the Dependent Frequency-Severity Model.”

Oh, Rosy, Kyung Suk Lee, Sojung C. Park, and Jae Youn Ahn. 2020. “Double-Counting Problem of the Bonus-Malus System.” Insurance: Mathematics and Economics 93: 141–55.

Oh, Rosy, Peng Shi, and Jae Youn Ahn. 2020. “Bonus-Malus Premiums Under the Dependent Frequency-Severity Modelling.” Scandinavian Actuarial Journal 2020(3): 172–95.

Pitrebois, Sandra, Michel Denuit, and Jean-François Walhin. 2003. “Setting a Bonus-Malus Scale in the Presence of Other Rating Factors: Taylor’s Work Revisited.” ASTIN Bulletin 33(2): 419–36.

Tan, Chong It. 2016. “Optimal Design of a Bonus-Malus System: Linear Relativities Revisited.” Annals of Actuarial Science 10(1): 52–64.

Tan, Chong It, Jackie Li, Johnny Siu-Hang Li, and Uditha Balasooriya. 2015. “Optimal Relativities and Transition Rules of a Bonus-Malus System.” Insurance: Mathematics and Economics 61: 255–63.