Chapter 15 Apéndice A: Revisión de la Inferencia Estadística
Vista previa del capítulo. El apéndice ofrece una visión general de los conceptos y métodos relacionados con la inferencia estadística sobre la población de interés, utilizando una muestra aleatoria de observaciones de la población. En el apéndice, la Sección 15.1 presenta los conceptos básicos relacionados con la población y la muestra utilizada para hacer la inferencia. La sección 15.2 presenta los métodos utilizados habitualmente para la estimación puntual de las características de la población. La sección 15.3 muestra la estimación de intervalos que tiene en cuenta la incertidumbre en la estimación, debido al uso de una muestra aleatoria de la población. La sección 15.4 presenta el concepto de prueba de hipótesis con el propósito de seleccionar variables y modelos.
15.1 Conceptos Básicos
En esta sección, aprenderemos los siguientes conceptos relacionados con la inferencia estadística.
- Muestreo aleatorio de una población que se puede resumir usando una lista de unidades o individuos dentro de la población
- Distribuciones de muestreo que caracterizan las distribuciones de posibles resultados para un estadístico calculada a partir de una muestra aleatoria
- El teorema central del límite que guía la distribución de la media de una muestra aleatoria de la población.
La inferencia estadística es el proceso de sacar conclusiones sobre las características de un gran conjunto de ítems/individuos (es decir, la población), utilizando un conjunto representativo de datos (por ejemplo, una muestra aleatoria) de una lista de ítems o individuos de la población que se pueden muestrear. Si bien el proceso tiene un amplio espectro de aplicaciones en diversas áreas, que incluyen ciencia, ingeniería, salud, ciencias sociales y economía, la inferencia estadística es importante para las compañías de seguros que usan datos de sus titulares de pólizas existentes para hacer inferencia sobre las características (p. ej., perfiles de riesgo) de un segmento específico de clientes objetivo (es decir, la población) a quienes las compañías de seguros no observan directamente.
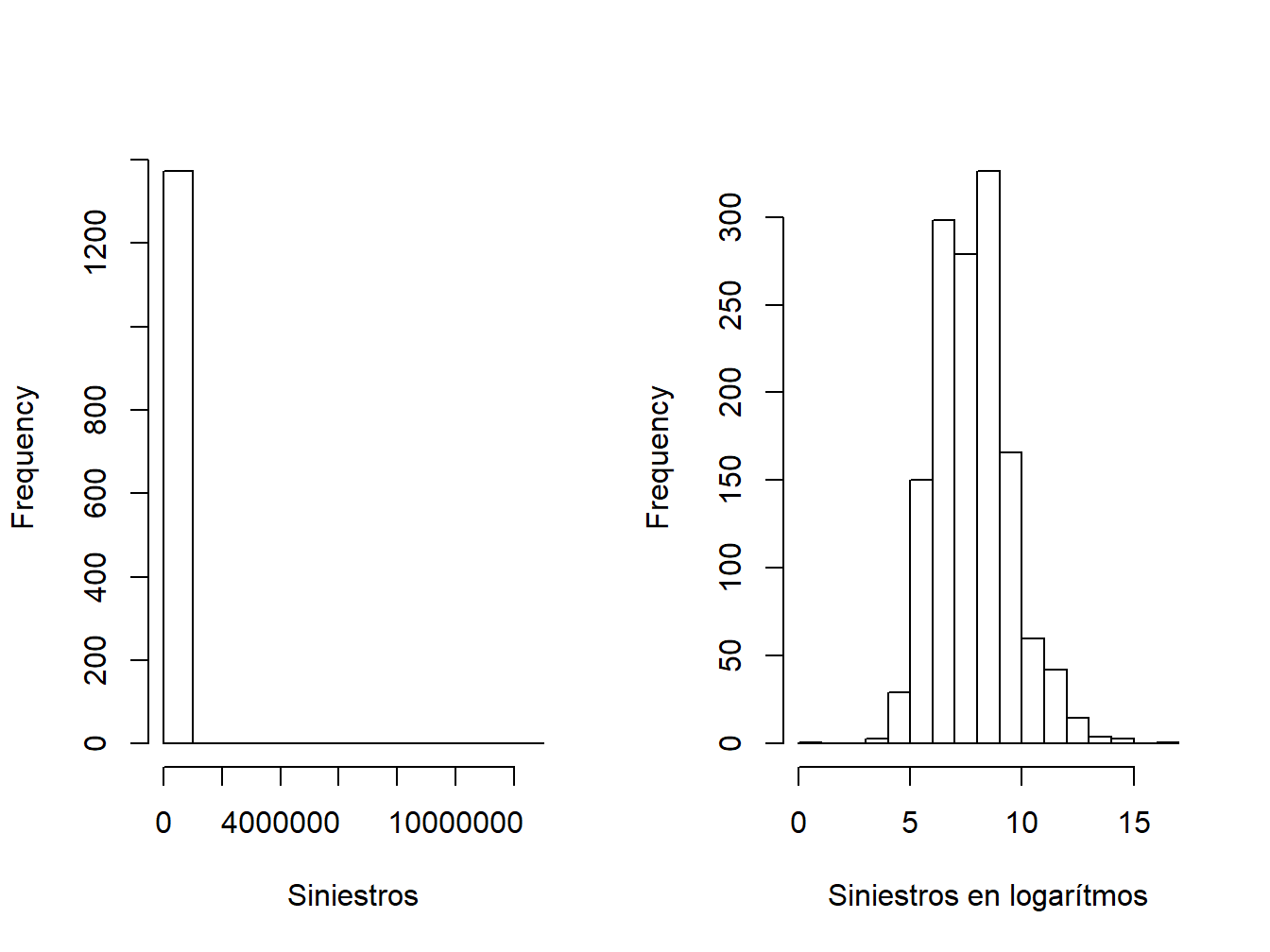
Mostrar ejemplo empírico usando el Wisconsin Property Fund
15.1.1 Muestreo Aleatorio
En estadística, se produce un error de muestreo cuando el marco de muestreo, la lista de la que se extrae la muestra, no es una aproximación adecuada de la población de interés. Una muestra debe ser un subconjunto representativo de una población, o universo, de interés. Si la muestra no es representativa, tomar una muestra más grande no elimina el sesgo, ya que el mismo error se repite una y otra vez. Por lo tanto, presentamos el concepto de muestreo aleatorio que da lugar a una simple muestra aleatoria que es representativa de la población.
Suponemos que la variable aleatoria \(X\) representa una elección de una población con una función de distribución \(F(\cdot)\) con media \(\mathrm{E}[X]=\mu\) y varianza \(\mathrm{Var}[X]=\mathrm{E}[(X-\mu)^2]\), donde \(E(\cdot)\) denota la esperanza de una variable aleatoria. En un muestreo aleatorio, hacemos un total de \(n\) sorteos o elecciones representados por \(X_1, \ldots, X_n\), cada uno de ellos no relacionados entre sí (es decir, estadísticamente independientes). Nos referimos a \(X_1, \ldots, X_n\) como una muestra aleatoria (con reemplazo) de \(F(\cdot)\), que toma una forma paramétrica o no paramétrica. Alternativamente, podemos decir que \(X_1, \ldots, X_n\) se distribuyen de forma idéntica e independiente (iid) con la función de distribución \(F(\cdot)\).
15.1.2 Distribución Muestral
Usando la muestra aleatoria \(X_1, \ldots, X_n\), estamos interesados en llegar a una conclusión sobre un atributo específico de la distribución de la población \(F(\cdot)\). Por ejemplo, podemos estar interesados en hacer una inferencia sobre la media de la población, denotada \(\mu\). Es natural pensar en la media muestral, \(\bar{X} = \sum_{i = 1}^n X_i\), como una estimación de la media de la población \(\mu\). Llamamos a la media de la muestra como estadístico calculado a partir de la muestra aleatoria \(X_1, \ldots, X_n\). Otros estadísticos de resumen de uso común incluyen la desviación estándar muestral y los cuantiles muestrales.
Cuando se utiliza un estadístico (por ejemplo, la media de la muestra \(\bar{X}\)) para hacer inferencia estadística sobre el atributo de la población (por ejemplo, la media de la población \(\mu\)), la calidad de la inferencia está determinada por el sesgo y la incertidumbre en la estimación, debido al uso de una muestra en lugar de la población. Por lo tanto, es importante estudiar la distribución de un estadístico que cuantifique el sesgo y la variabilidad del estadístico. En particular, la distribución de la media muestral, \(\bar {X}\) (o cualquier otro estadístico), se llama distribución muestral. La distribución muestral depende del proceso de muestreo, el estadístico, el tamaño de la muestra \(n\) y la distribución de la población \(F(\cdot )\). El teorema central del límite proporciona la distribución en muestras grandes (muestral) de la media muestral bajo ciertas condiciones.
15.1.3 Teorema Central del Límite
En estadística, existen variaciones del teorema central del límite (TCL) que aseguran que, bajo ciertas condiciones, la media de la muestra se acercará a la media de la población con su distribución muestral acercándose a la distribución normal a medida que el tamaño de la muestra tienda a infinito. Exponemos el TCL de Lindeberg - Levy que establece la distribución muestral asintótica de la media de la muestra \(\bar{X}\) calculada usando una muestra aleatoria de una población universal que tiene una distribución \(F(\cdot)\).
TCL de Lindeberg–Levy. Sea \(X_1, \ldots, X_n\) una muestra aleatoria de una distribución \(F(\cdot)\) con media \(\mu\) y varianza \(\sigma^2<\infty\). La diferencia entre la media muestral \(\bar{X}\) y \(\mu\), cuando se multiplica por \(\sqrt{n}\), converge en distribución a una distribución normal a medida que el tamaño de la muestra tiende a infinito. Es decir, \[\sqrt{n}(\bar{X}-\mu)\xrightarrow[]{d}N(0,\sigma).\]
Hay que tener en cuenta que el TCL no requiere una forma paramétrica para \(F(\cdot)\). Con base al TCL, podemos realizar inferencia estadística sobre la media de la población (inferimos, no deducimos). Los tipos de inferencia que podemos realizar incluyen estimación de la población, contraste de hipótesis sobre si una afirmación nula es verdadera y predicción de muestras futuras de la población.
15.2 Estimación Puntual y Propiedades
En esta sección, aprendemos cómo
- estimar parámetros poblacionales utilizando el método de estimación de momentos
- estimar parámetros poblacionales basados en la estimación de máxima verosimilitud
La función de distribución de población \(F(\cdot)\) generalmente se puede caracterizar por un número limitado (finito) de terminos llamados parámetros, en cuyo caso nos referimos a la distribución como una distribución paramétrica. En cambio, en el análisis no paramétrico, los atributos de la distribución muestral no se limitan a un pequeño número de parámetros.
Para obtener las características de la población, existen diferentes atributos relacionados con la distribución poblacional \(F(\cdot)\). Dichas medidas incluyen la media, la mediana, los percentiles (es decir, el percentil 95) y la desviación estándar. Dado que estas medidas de resumen no dependen de un parámetro específico, son medidas de resumen no paramétricas.
En el análisis paramétrico, por otro lado, podemos suponer familias específicas de distribuciones con parámetros específicos. Por ejemplo, generalmente se piensa que el logaritmo de las cuantías de los siniestros se distribuye normalmente con una media \(\mu\) y una desviación estándar \(\sigma\). Es decir, suponemos que los siniestros tienen una distribución lognormal con parámetros \(\mu\) y \(\sigma\). Alternativamente, las compañías de seguros suelen suponer que la gravedad de un siniestro sigue una distribución gamma con un parámetro de forma \(\alpha\) y un parámetro de escala \(\theta\). Aquí, las distribuciones normal, lognormal y gamma son ejemplos de distribuciones paramétricas. En los ejemplos anteriores, las cuantías \(\mu\), \(\sigma\), \(\alpha\) y \(\theta\) se conocen como parámetros. Para una familia de distribución paramétrica dada, la distribución está determinada únicamente por los valores de los parámetros.
A menudo se usa \(\theta\) para denotar un atributo de resumen de la población. En los modelos paramétricos, \(\theta\) puede ser un parámetro o una función de parámetros de una distribución como los parámetros de la media y varianza en la normal. En el análisis no paramétrico, puede tomar la forma de una medida resumen no paramétrica, como la media de la población o la desviación estándar. Supongamos que \(\hat {\theta} = \hat {\theta} (X_1, \ldots, X_n)\) es una función de la muestra que proporciona una proxy, o una estimación, de \(\theta\). Toda función de la muestra \(X_1, \ldots, X_n\) se conoce como estadístico.
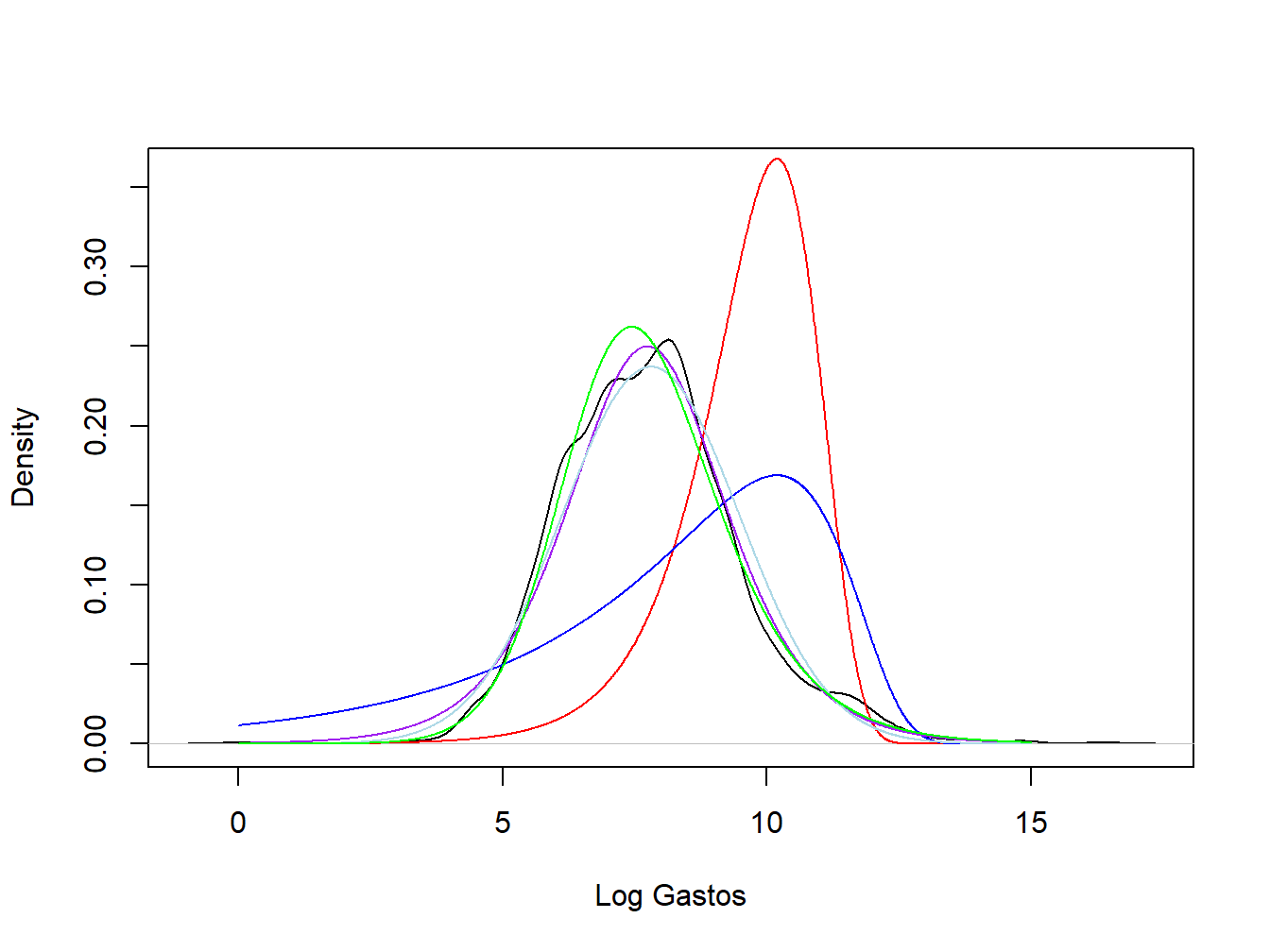
Mostrar ejemplo Wisconsin Property Fund - Continuación
15.2.1 Método de Estimación de Momentos
Antes de definir el método de estimación de momentos, definimos el concepto de momentos. Los momentos son atributos de la población que caracterizan la función de distribución \(F(\cdot)\). Dado una elección aleatoria \(X\) de \(F(\cdot)\), la esperanza \(\mu_k = \ mathrm {E} [X^k]\) se llama momento \(k\)-ésimo de \(X\), \(k = 1,2,3, \ldots\) Por ejemplo, la media poblacional \(\mu\) es el primer momento. Además, la esperanza \(\mathrm{E}[(X-\mu)^k]\) se denomina momento central \(k\)-ésimo. Por lo tanto, la varianza es el segundo momento central.
Usando la muestra aleatoria \(X_1, \ldots, X_n\), podemos construir el momento muestral correspondiente, \(\hat {\mu}_k = (1 / n) \sum_{i = 1}^n X_i^k\), para estimar el atributo de población \(\mu_k\). Por ejemplo, hemos utilizado la media muestral \(\bar {X}\) como estimador de la media poblacional \(\mu\). Del mismo modo, el segundo momento central puede estimarse como \((1 / n) \sum_{i = 1}^n(X_i- \bar {X})^2\). Sin asumir una forma paramétrica para \(F (\cdot)\), los momentos muestrales constituyen estimaciones no paramétricas de los atributos de la población correspondiente. Dicho estimador basado en la coincidencia entre los momentos de la muestra correspondiente y los de la población se llama método de estimador de momentos (MEM).
Si bien el MEM funciona de forma natural en un modelo no paramétrico, se puede usar para estimar parámetros cuando se supone una familia de distribución paramétrica específica \(F(\cdot)\). Denotamos por \(\boldsymbol{\theta}=(\theta_1,\cdots,\theta_m)\) al vector de parámetros correspondiente a una distribución paramétrica \(F(\cdot)\). Dada una familia de distribuciones, habitualmente se conoce las relaciones entre los parámetros y los momentos. En particular, conocemos las formas específicas de las funciones \(h_1(\cdot),h_2(\cdot),\cdots,h_m(\cdot)\) tales que \(\mu_1=h_1(\boldsymbol{\theta}),\,\mu_2=h_2(\boldsymbol{\theta}),\,\cdots,\,\mu_m=h_m(\boldsymbol{\theta})\). Dado el MEM \(\hat{\mu}_1, \ldots, \hat{\mu}_m\) de la muestra aleatoria, el MEM de los parámetros \(\hat{\theta}_1,\cdots,\hat{\theta}_m\) se puede obtener resolviendo las ecuaciones \[\hat{\mu}_1=h_1(\hat{\theta}_1,\cdots,\hat{\theta}_m);\] \[\hat{\mu}_2=h_2(\hat{\theta}_1,\cdots,\hat{\theta}_m);\] \[\cdots\] \[\hat{\mu}_m=h_m(\hat{\theta}_1,\cdots,\hat{\theta}_m).\]
Mostrar ejemplo Wisconsin Property Fund - Continuación
15.2.2 Estimación por Máxima Verosimilitud
Cuando \(F(\cdot)\) toma forma paramétrica, habitualmente se usa el método de máxima verosimilitud para estimar los parámetros de la población \(\boldsymbol {\theta}\). La estimación máximo verosímil se basa en la función de verosimilitud, una función de los parámetros dada la muestra observada. Denotamos por \(f(x_i| \boldsymbol {\theta})\) a la función de probabilidad de \(X_i\) evaluada en \(X_i = x_i\) \((i = 1,2, \cdots, n)\) es la función de masa de probabilidad en el caso de una \(X\) discreta y la función de densidad de probabilidad en el caso de una \(X\) continua. Suponiendo independencia, la función de verosimilitud de \(\boldsymbol{\theta}\) asociada a la observación \((X_1,X_2,\cdots,X_n)=(x_1,x_2,\cdots,x_n)=\mathbf{x}\) se puede escribir como
\[L(\boldsymbol{\theta}|\mathbf{x})=\prod_{i=1}^nf(x_i|\boldsymbol{\theta}),\] con la correspondiente función de log-verosimilitud dada por \[l(\boldsymbol{\theta}|\mathbf{x})=\ln(L(\boldsymbol{\theta}|\mathbf{x}))=\sum_{i=1}^n\ln f(x_i|\boldsymbol{\theta}).\]
El estimador de máxima verosimilitud (EMV, en inglés MLE) de \(\boldsymbol{\theta}\) es el conjunto de valores de \(\boldsymbol {\theta}\) que maximizan la función de verosimilitud (función log-verosimilitud), dada la muestra observada. Es decir, el MLE \(\hat {\boldsymbol {\theta}}\) se puede escribir como \[\hat{\boldsymbol{\theta}}={\mbox{argmax}}_{\boldsymbol{\theta}\in\Theta}l(\boldsymbol{\theta}|\mathbf{x}),\] donde \(\Theta\) es el espacio de parámetros de \(\boldsymbol {\theta}\) y \({\mbox{argmax}}_{\boldsymbol{\theta}\in\Theta}l(\boldsymbol{\theta}|\mathbf{x})\) se define como el valor de \(\boldsymbol {\theta}\) en el cual la función \(l(\boldsymbol {\theta} | \mathbf {x})\) alcanza su máximo.
Dada la forma analítica de la función de verosimilitud, el MLE se puede obtener tomando la primera derivada de la función de verosimilitud con respecto a \(\boldsymbol {\theta}\), e igualando los valores de las derivadas parciales a cero. Es decir, los MLE son las soluciones de las siguientes ecuaciones \[\frac{\partial l(\hat{\boldsymbol{\theta}}|\mathbf{x})}{\partial\hat{\theta}_1}=0;\] \[\frac{\partial l(\hat{\boldsymbol{\theta}}|\mathbf{x})}{\partial\hat{\theta}_2}=0;\] \[ \cdots \] \[\frac{\partial l(\hat{\boldsymbol{\theta}}|\mathbf{x})}{\partial\hat{\theta}_m}=0,\] siempre que las segundas derivadas parciales sean negativas.
Para los modelos paramétricos, el estimador MLE de los parámetros puede obtenerse analíticamente (por ejemplo, en el caso de distribuciones normales y estimadores lineales) o numéricamente mediante algoritmos iterativos como el método de Newton-Raphson y sus versiones adaptativas (por ejemplo, en el caso de modelos lineales generalizados con una variable de respuesta no normal).
Distribución Normal. Supongamos que \((X_1,X_2,\cdots,X_n)\) es una muestra aleatoria de la distribución normal \(N(\mu, \sigma^2)\). Con una muestra observada \((X_1,X_2,\cdots,X_n)=(x_1,x_2,\cdots,x_n)\), podemos escribir la función de verosimilitud de \(\mu,\sigma^2\) como \[L(\mu,\sigma^2)=\prod_{i=1}^n\left[\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\left(x_i-\mu\right)^2}{2\sigma^2}}\right],\] con la correspondiente función de log-verosimilitud dada por \[l(\mu,\sigma^2)=-\frac{n}{2}[\ln(2\pi)+\ln(\sigma^2)]-\frac{1}{2\sigma^2}\sum_{i=1}^n\left(x_i-\mu\right)^2.\]
Resolviendo
\[\frac{\partial l(\hat{\mu},\sigma^2)}{\partial \hat{\mu}}=0,\] obtenemos \(\hat{\mu}=\bar{x}=(1/n)\sum_{i=1}^nx_i\). Es sencillo verificar que \(\frac{\partial l^2(\hat{\mu},\sigma^2)}{\partial \hat{\mu}^2}\left|_{\hat{\mu}=\bar{x}}\right.<0\). Como el mismo razonamiento funciona para cualquier \(x\) arbitrario, \(\hat{\mu}=\bar{X}\) es el estimador MLE de \(\mu\). Del mismo modo, resolviendo \[\frac{\partial l(\mu,\hat{\sigma}^2)}{\partial \hat{\sigma}^2}=0,\] obtenemos \(\hat{\sigma}^2=(1/n)\sum_{i=1}^n(x_i-\mu)^2\). Además, reemplazando \(\mu\) por \(\hat {\mu}\), obtenemos el estimador MLE de \(\sigma^2\) como \(\hat{\sigma}^2=(1/n)\sum_{i=1}^n(X_i-\bar{X})^2\).
Por lo tanto, la media de la muestra \(\bar{X}\) y \(\hat{\sigma}^ 2\) son tanto estimadores MEM como MLE para la media \(\mu\) y la varianza \(\sigma^2\), bajo el supuesto de una distribución de población normal \(F(\cdot)\). En el Apéndice del Capítulo 16 se proporcionan más detalles sobre las propiedades de la función de verosimilitud y la derivación de MLE bajo distribuciones paramétricas distintas de la distribución normal.
15.3 Estimación de Intervalo
En esta sección, se aprende como
- derivar la distribución muestral exacta del MLE de la media normal
- obtener la aproximación para muestra grande de la distribución muestral utilizando las propiedades de muestra grande del MLE
- construir un intervalo de confianza de un parámetro basado en las propiedades de las muestras de tamaño elevado para el MLE
Ahora que hemos introducido el estimador MEM y el estimador MLE, podemos realizar el primer tipo de inferencia estadística, estimación por intervalo que cuantifica la incertidumbre resultante del uso de una muestra finita. Derivando la distribución muestral del estimador MLE, se puede estimar un intervalo (un intervalo de confianza) para el parámetro. Bajo el enfoque frecuentista (por ejemplo, el basado en la estimación de máxima verosimilitud), los intervalos de confianza generados a partir del mismo marco de muestreo aleatorio cubrirán el valor verdadero la mayoría de las veces (por ejemplo, el 95% de las veces), si repetimos el proceso de muestreo y volvemos a calcular el intervalo una y otra vez. Dicho proceso requiere la derivación de la distribución muestral para el estimador MLE.
15.3.1 Distribución Exacta para la Media de Muestra Normal
Debido a la propiedad de aditividad de la distribución normal (es decir, una suma de variables aleatorias normales que sigue una distribución normal multivariante tiene una distribución normal) y que la distribución normal pertenece a la familia de localización-escala (es decir, un cambio de ubicación y/o de escala de una variable aleatoria normal tiene una distribución normal), la media muestral \(\bar {X}\) de una muestra aleatoria de una \(F(\cdot)\) normal tiene una distribución muestral normal para cualquier valor finito \(n\). Dado \(X_i \sim^{iid} N(\mu, \sigma^2)\), \(i = 1, \dots, n\), el estimador MLE de \(\mu\) tiene una distribución exacta \[\bar{X} \sim N \left (\mu, \frac {\sigma^2} {n} \right).\] Por lo tanto, la media muestral es un estimador insesgado de \(\mu\). Además, la incertidumbre en la estimación se puede cuantificar mediante su varianza \(\sigma^2 / n\), que disminuye con el tamaño de la muestra \(n\). Cuando el tamaño de la muestra tiende a infinito, la media muestral se acercará en una sola masa al valor verdadero.
15.3.2 Propiedades de Muestra Grande del Estimador MLE
No obstante, para el estimador MLE del parámetro de la media y cualquier otro parámetro de otras familias de distribución paramétrica, generalmente no podemos derivar una distribución muestral exacta para muestras finitas. Afortunadamente, cuando el tamaño de la muestra es suficientemente grande, los estimadores MLE pueden aproximarse mediante una distribución normal. Debido a la teoría general de máxima verosimilitud, el MLE tiene algunas buenas propiedades para muestras grandes.
El estimador MLE \(\hat {\theta}\) de un parámetro \(\theta\), es un estimador consistente. Es decir, \(\hat {\theta}\) converge en probabilidad al valor verdadero \(\theta\), cuando el tamaño de la muestra \(n\) tiende a infinito.
El MLE cumple la propiedad de normalidad asintótica, lo que significa que el estimador convergerá en distribución a una distribución normal centrada alrededor del valor verdadero, cuando el tamaño de la muestra tienda a infinito. Es decir, \[\sqrt{n}(\hat{\theta}-\theta)\rightarrow_d N\left(0,\,V\right),\quad \mbox{as}\quad n\rightarrow \infty,\] donde \(V\) es la inversa de la información de Fisher. Por lo tanto, el estimador MLE \(\hat {\theta}\) sigue aproximadamente una distribución normal con una media \(\theta\) y una varianza \(V / n\), cuando el tamaño de la muestra es grande.
El estimador MLE es eficiente, lo que significa que tiene la varianza asintótica más pequeña posible, \(V\), denominada frecuentemente la cota inferior de Cramer-Rao. En particular, la cota inferior de Cramer-Rao es la inversa de la información de Fisher definida como \(\mathcal{I}(\theta)=-\mathrm{E}(\partial^2\ln f(X;\theta)/\partial \theta^2)\). Por lo tanto, \(\mathrm{Var}(\hat{\theta})\) se puede estimar en función de la información de Fisher observada que se puede escribir como \(-\sum_{i=1}^n \partial^2\ln f(X_i;\theta)/\partial \theta^2\).
Para muchas distribuciones paramétricas, la información de Fisher puede derivarse analíticamente para el estimador MLE de los parámetros. Para modelos paramétricos más sofisticados, la información de Fisher se puede evaluar numéricamente mediante la integración numérica para distribuciones continuas, o la suma numérica para distribuciones discretas.
15.3.3 Intervalo de confianza
Dado que el estimador MLE \(\hat{\theta}\) tiene una distribución normal exacta o aproximada con una media \(\theta\) y una varianza \(\mathrm{Var} (\hat {\theta})\), podemos tomar la raíz cuadrada de la varianza e incorporar la estimación para definir \(se (\hat {\theta}) = \sqrt {\mathrm {Var} (\hat {\theta})}\). Un error estándar es una desviación estándar estimada que cuantifica la incertidumbre en la estimación resultante del uso de una muestra finita. Bajo algunas condiciones de regularidad que rigen la distribución de la población, podemos establecer que el estadístico \[\frac {\hat {\theta} - \theta} {se (\hat {\theta})}\] converge en distribución a una distribución \(t\)-Student con \({np}\) grados de libertad (un parámetro de la distribución), donde \(p\) es el número de parámetros en el modelo distintos a la varianza. Por ejemplo, para el caso de la distribución normal, tenemos \(p = 1\) para el parámetro \(\mu\); para un modelo de regresión lineal con una variable independiente, tenemos \(p = 2\) para los parámetros de la intersección y la variable independiente. Si denotamos por \(t_{np} (1- \alpha / 2)\) el \(100 \times (1- \alpha / 2)\)-ésimo percentil de la distribución \(t\)-Student que satisface \(\Pr\left[t< t_{n-p}\left(1-{\alpha}/{2}\right) \right]= 1-{\alpha}/{2}\). Tenemos,
\[\Pr\left[-t_{n-p}\left(1-\frac{\alpha}{2}\right)<\frac{\hat{\theta}-\theta}{se(\hat{\theta})}< t_{n-p}\left(1-\frac{\alpha}{2}\right) \right]= 1-{\alpha},\] de donde podemos derivar un intervalo de confianza para \(\theta\). De la ecuación anterior podemos derivar un par de estadísticos, \(\hat{\theta}_1\) y \(\hat {\theta}_2\), que proporcionan un intervalo de la forma \([\hat{\theta}_1, \hat{\theta}_2]\). Este intervalo es un intervalo de confianza de nivel \(1-\alpha\) para \(\theta\) tal que \(\Pr\left(\hat{\theta}_1 \le \theta \le \hat{\theta}_2\right) = 1-\alpha,\) donde la probabilidad \(1-\alpha\) se conoce como el nivel de confianza. Hay que tener en cuenta que el intervalo de confianza anterior no es válido para muestras pequeñas, excepto para el caso de la media normal.
Distribución Normal. Para la media de la población normal \(\mu\), el estimador MLE tiene una distribución muestral exacta \(\bar{X}\sim N(\mu,\sigma/\sqrt{n})\), en la que podemos estimar \(se (\hat {\theta})\) mediante \(\hat {\sigma} / \sqrt {n}\). Basándonos en el teorema de Cochran, el estadístico resultante tiene una distribución exacta \(t\)-Student con \(n-1\) grados de libertad. Por lo tanto, podemos derivar los límites inferior y superior del intervalo de confianza como \[\hat{\mu}_1 = \hat{\mu} - t_{n-1}\left(1-\frac{\alpha}{2}\right)\frac{ \hat{\sigma}}{\sqrt{n}}\] y \[\hat{\mu}_2 = \hat{\mu} + t_{n-1}\left(1-\frac{\alpha}{2}\right)\frac{ \hat{\sigma}}{\sqrt{n}}.\] Cuando \(\alpha = 0,05\), \(t_{n-1} (1- \alpha / 2) \approx 1,96\) para valores grandes de \(n\). Por el teorema de Cochran, el intervalo de confianza es válido independientemente del tamaño de la muestra.
Mostrar ejemplo del Wisconsin Property Fund - Continuación
15.4 Pruebas de Hipótesis
En esta sección, se aprende cómo
- comprender los conceptos básicos en la prueba de hipótesis, incluido el nivel de significación y la potencia de una prueba
- realizar pruebas de hipótesis como un contraste \(t\)-Student basado en las propiedades del estimador MLE
- construir una prueba de la razón de verosimilitud para un solo parámetro o múltiples parámetros del mismo modelo estadístico
- utilizar criterios de información como el criterio de información de Akaike o el criterio de información bayesiano para realizar la selección del modelo
Para los parámetros \(\boldsymbol {\theta}\) de una distribución paramétrica, un tipo alternativo de inferencia estadística que se llama prueba de hipótesis verifica si una hipótesis con respecto a los parámetros es verdadera, bajo una probabilidad dada llamada nivel de significación \(\alpha\) (por ejemplo, 5%). En las pruebas de hipótesis, rechazamos la hipótesis nula, una afirmación restrictiva sobre los parámetros, si la probabilidad de observar una muestra aleatoria tan extrema como la observada es menor que \(\alpha\), si la hipótesis nula fuera cierta.
15.4.1 Conceptos Básicos
En un test estadístico, generalmente estamos interesados en probar si una afirmación con respecto a algunos parámetros, una hipótesis nula (denotada por \(H_0\)), es verdadera dados los datos observados. La hipótesis nula puede tomar una forma general \(H_0:\theta\in\Theta_0\), donde \(\Theta_0\) es un subconjunto del espacio de parámetros \(\Theta\) de \(\theta\) que puede contener múltiples parámetros. Para el caso de un solo parámetro \(\theta\), la hipótesis nula generalmente toma la forma \(H_0: \theta = \theta_0\) o \(H_0: \theta \leq \theta_0\). Lo opuesto a la hipótesis nula se llama hipótesis alternativa que se puede escribir como \(H_a: \theta \neq \theta_0\) o \(H_a: \theta> \theta_0\). La prueba estadística en \(H_0: \theta = \theta_0\) se llama de dos colas ya que la hipótesis alternativa contiene dos desigualdades de la \(H_a: \theta <\theta_0\) o \(\theta> \theta_0\). Por el contrario, la prueba estadística en \(H_0: \theta \leq \theta_0\) o \(H_0: \theta \geq \theta_0\) se llama prueba de una cola.
Una prueba estadística generalmente se construye en base a un estadístico \(T\) y su distribución muestral exacta o de gran tamaño. El contraste generalmente rechaza una prueba de dos colas cuando \(T> c_1\) o \(T <c_2\), donde las dos constantes \(c_1\) y \(c_2\) se obtienen en función de la distribución muestral de \(T\) a un nivel de probabilidad \(\alpha\) llamado nivel de significación. En particular, el nivel de significación \(\alpha\) satisface \[\alpha=\Pr(\mbox{rechazar }H_0|H_0\mbox{ es cierta}),\] lo que significa que si la hipótesis nula fuese cierta, rechazaríamos la hipótesis nula solo el 5% de las veces, si repetimos el proceso de muestreo y realizamos la prueba una y otra vez.
Por lo tanto, el nivel de significación es la probabilidad de cometer un error tipo I (error del primer tipo), el error de rechazar incorrectamente una hipótesis nula verdadera. Por esta razón, el nivel de significación \(\alpha\) también se conoce como el porcentaje de error tipo I. Otro tipo de error que podemos cometer en la prueba de hipótesis es el error tipo II (error del segundo tipo), el error de aceptar incorrectamente una hipótesis nula falsa. De manera similar, podemos definir el porcentaje de error de tipo II como la probabilidad de no rechazar (aceptar) una hipótesis nula cuando no es cierta. Es decir, el porcentaje de error tipo II viene dada por \[\Pr (\mbox {aceptar } H_0 | H_0 \mbox { es falsa}).\] Otro importante valor con respecto a la calidad de la prueba estadística se llama potencia del contraste \(\beta\), definida como la probabilidad de rechazar una hipótesis nula falsa. La definición matemática de la potencia es \[\beta = \Pr (\mbox {rechazar } H_0 | H_0 \mbox { es falsa}).\] Hay que tener en cuenta que la potencia del contraste generalmente se calcula en función de un valor alternativo específico de \(\theta = \theta_a\), dada una distribución muestral específica y un tamaño de muestra dado. En estudios experimentales reales, generalmente se calcula el tamaño muestral requerido para elegir un tamaño de muestra que garantice una elevada posibilidad de obtener una prueba estadísticamente significativa (es decir, con una potencia estadística preespecificada como el 85%).
15.4.2 Contraste \(t\)-Student Basado en el Estimador MLE
En base a los resultados de la Sección 15.3.1, podemos definir un contraste \(t\) de Student para probar que se cumple \(H_0: \theta = \theta_0\). En particular, definimos el estadístico de prueba como \[t\text{-stat}=\frac{\hat{\theta}-\theta_0}{se(\hat{\theta})},\]
que tiene como distribución para muestra grande una distribución \(t\)-Student con \({np}\) grados de libertad, cuando la hipótesis nula es verdadera (es decir, cuando \(\theta = \theta_0\)).
Para un nivel de significación \(\alpha\), por ejemplo 5%, rechazamos la hipótesis nula si se cumple \(t\text{-stat}<-t_{n-p}\left(1-{\alpha}/{2}\right)\) o \(t\text{-stat}> t_{n-p}\left(1-{\alpha}/{2}\right)\) (la región de rechazo). Bajo la hipótesis nula \(H_0\), tenemos \[\Pr\left[t\text{-stat}<-t_{n-p}\left(1-\frac{\alpha}{2}\right)\right]=\Pr\left[t\text{-stat}> t_{n-p}\left(1-\frac{\alpha}{2}\right) \right]= \frac{\alpha}{2}.\] Además del concepto de región de rechazo, podemos rechazar el test a partir del \(p\)-valor definido como \(2\Pr(T>|t\text{-stat}|)\) para el contraste a dos colas mencionado anteriormente, donde la variable aleatoria \(T \sim T_{np}\). Rechazamos la hipótesis nula si el \(p\)-valor es menor o igual a \(\alpha\). Para una muestra dada, el \(p\)-valor se define como el nivel de significación más pequeño para el cual la hipótesis nula sería rechazada.
Del mismo modo, podemos construir una prueba a una cola para la hipótesis nula \(H_0:\theta\leq\theta_0\) (o \(H_0:\theta\geq\theta_0\)). Usando el mismo estadístico de prueba, rechazamos la hipótesis nula cuando \(t\text{-stat}> t_{n-p}\left(1-{\alpha}\right)\) (o \(t\text{-stat}<- t_{n-p}\left(1-{\alpha}\right)\) para la prueba \(H_0:\theta\geq\theta_0\)). El \(p\)-valor correspondiente se define como \(\Pr(T>|t\text{-stat}|)\) (o \(\Pr(T<|t\text{-stat}|)\) para el contraste en \(H_0:\theta\geq\theta_0\)). Hay que tener en cuenta que la prueba no es válida para muestras pequeñas, excepto para el caso de la prueba para la media normal.
Test \(t\) en una muestra para la media Normal. Para el test de la media normal de la forma \(H_0:\mu=\mu_0\), \(H_0:\mu\leq\mu_0\) o \(H_0:\mu\geq\mu_0\), podemos definir el estadístico del contraste como \[t\text{-stat}=\frac{\bar{X}-\mu_0}{{\hat{\sigma}}/{\sqrt{n}}},\] para el cual tenemos una distribución muestral exacta \(t\text{-stat}\sim T_{n-1}\) por el teorema de Cochran, con \(T_ {n-1}\) que denota una distribución \(t\)-Student con \(n-1\) grados de libertad. Según el teorema de Cochran, la prueba es válida tanto para muestras pequeñas como grandes.
Mostrar ejemplo de Wisconsin Property Fund - Continuación
Mostrar ejemplo Wisconsin Property Fund - Continuación
15.4.3 Prueba de la Razón de Verosimilitud
En la subsección anterior, hemos introducido la prueba \(t\)-Student para un único parámetro, basada en las propiedades del estimador MLE. En esta sección, definimos un contraste alternativo llamado prueba de la razón de verosimilitud (LRT, por sus siglas en inglés). La LRT se puede usar para contrastar múltiples parámetros del mismo modelo estadístico.
Dada la función de verosimilitud \(L(\theta|\mathbf{x})\) y \(\Theta_0 \subset \Theta\), el estadístico de prueba de la razón de probabilidad para contrastar \(H_0:\theta\in\Theta_0\) frente a \(H_a:\theta\notin\Theta_0\) viene dado por \[L=\frac{\sup_{\theta\in\Theta_0}L(\theta|\mathbf{x})}{\sup_{\theta\in\Theta}L(\theta|\mathbf{x})},\] y de manera similar, para contrastar \(H_0:\theta=\theta_0\) frente a \(H_a:\theta\neq\theta_0\) es \[L=\frac{L(\theta_0|\mathbf{x})}{\sup_{\theta\in\Theta}L(\theta|\mathbf{x})}.\] El contraste LRT rechaza la hipótesis nula cuando \(L <c\), con el umbral dependiendo del nivel de significación \(\alpha\), el tamaño de la muestra \(n\) y el número de parámetros en \(\theta\). Basándonos en el Lema de Neyman-Pearson, la LRT es la prueba uniformemente más potente (UMP) para contrastar \(H_0: \theta = \theta_0\) frente a \(H_a: \theta = \theta_a\). Es decir, proporciona la mayor potencia \(\beta\) para un determinado \(\alpha\) y un valor alternativo dado \(\theta_a\).
Basándonos en el Teorema de Wilks, el estadístico de prueba de la razón de verosimilitud \(-2\ln (L)\) converge en distribución a una distribución Chi-cuadrado con tantos grados de libertad como la diferencia entre la dimensionalidad de los espacios de parámetros \(\Theta\) y \(\Theta_0\), cuando el tamaño de la muestra tiende a infinito y cuando el modelo nulo está anidado dentro del modelo alternativo. Es decir, cuando el modelo nulo es un caso especial del modelo alternativo que contiene un espacio muestral restringido, podemos aproximar \(c\) por \(\chi^2_{p_1 - p_2} (1-\alpha)\), el \(100 \times (1- \alpha)\)-ésimo percentil de la distribución Chi-cuadrado, con \(p_1-p_2\) grados de libertad, tomando \(p_1\) y \(p_2\) como los correspondientes números de parámetros en los modelos alternativo y nulo respectivamente. Se ha de tener en cuenta que la LRT también es un contraste asintótico que no será válido para muestras pequeñas.
15.4.4 Criterios de Información
En aplicaciones reales, la LRT se usa frecuentemente para comparar dos modelos anidados. Sin embargo, el enfoque LRT como herramienta de selección de modelos tiene dos inconvenientes fundamentales: 1) Por lo general, requiere que el modelo nulo esté anidado dentro del modelo alternativo; 2) los modelos seleccionados mediante la LRT tienden a proporcionar un ajuste excesivo (sobreajuste) dentro de la muestra, lo que conduce a una predicción deficiente fuera de la muestra. Para superar estos problemas, la selección del modelo basada en criterios de información, aplicable a modelos no anidados y teniendo en cuenta la complejidad del modelo, se usa más ampliamente para la selección del modelo que la LRT. Aquí, presentamos los dos criterios más utilizados, el criterio de información de Akaike y el criterio de información bayesiano.
En particular, el criterio de información de Akaike (\(AIC\)) se define como \[AIC = -2\ln L(\hat{\boldsymbol \theta}) + 2p,\] donde \(\hat{\boldsymbol \theta}\) denota el estimador MLE de \({\boldsymbol \theta}\), y \(p\) es el número de parámetros del modelo. El término adicional \(2p\) representa una penalización por la complejidad del modelo. Es decir, con la misma función de verosimilitud maximizada, el \(AIC\) favorece el modelo con menos parámetros. Nótese que \(AIC\) no tiene en cuenta el impacto del tamaño de la muestra \(n\).
Alternativamente, se usa el criterio de información bayesiano (\(BIC\)) que toma en consideración el tamaño de la muestra. El \(BIC\) se define como \[BIC = -2\ln L(\hat{\boldsymbol \theta}) + p\,\ln(n).\] Observamos que el \(BIC\) generalmente asigna un mayor peso al número de parámetros. Con la misma función de verosimilitud maximizada, el \(BIC\) sugerirá un modelo más parsimonioso que el \(AIC\).
Mostrar ejemplo Wisconsin Property Fund - Continuación
Autoría
Lei (Larry) Hua, Northern Illinois University, y Edward W. (Jed) Frees, University of Wisconsin-Madison, son los autores principales de la versión inicial de este capítulo. Email: lhua@niu.edu o jfrees@bus.wisc.edu para enviar comentarios o sugerencias de mejora.
Traducción al español: Montserrat Guillen y Manuela Alcañiz (Universitat de Barcelona).