Chapter 4 Selección del Modelo y Estimación

Vista Previa del Capítulo. En los Capítulos 2 y 3 se han descrito cómo ajustar los modelos paramétricos a datos que miden, respectivamente, la frecuencia y la severidad de los eventos analizados. Este capítulo se centra en la selección de los modelos. Inicialmente, para comparar modelos paramétricos alternativos, es útil describir los datos sin referencia a una distribución paramétrica específica. La Sección 4.1 describe en que consiste la estimación no paramétrica, cómo podemos usarla para comparar modelos paramétricos alternativos y cómo, a partir de la misma, pueden obtenerse valores iniciales que permitan implementar procedimientos paramétricos. El proceso de selección del modelo se resume en la Sección 4.2. Aunque la descripción se centra en el análisis de datos continuos, el mismo procedimiento puede usarse para datos discretos o datos que provienen de una combinación híbrida de datos discretos y continuos.

La selección y la estimación del modelo son aspectos fundamentales de la modelización estadística. Para proporcionar una idea de cómo se pueden adaptar a esquemas de muestreo alternativos, la Sección 4.3 describe la estimación con datos agrupados, censurados y truncados (siguiendo la introducción de la Sección 3.5). Para ver cómo los procedimientos de selección y estimación se pueden adaptar a modelos alternativos, el capítulo se cierra con la Sección 4.4 sobre inferencia bayesiana, un procedimiento alternativo donde los parámetros (típicamente desconocidos) se tratan como variables aleatorias.

4.1 Inferencia No Paramétrica

---

En esta sección se aprende a:

• Estimación de momentos, cuantiles y distribuciones sin referencia a una distribución paramétrica.
• Resumir los datos gráficamente sin referencia a una distribución paramétrica
• Determinar medidas que resuman las desviaciones de un ajuste paramétrico de un ajuste no paramétrico
• Use estimadores no paramétricos para aproximar los parámetros que se pueden usar para iniciar un procedimiento de estimación paramétrica

---

4.1.1 Estimación No Paramétrica

En la Sección 2.2 para la frecuencia y en la Sección 3.1 para la severidad, aprendimos cómo describir una distribución mediante el cálculo de las medias, las varianzas, los cuantiles/percentiles, etc.. Para aproximar estas medidas de resumen utilizando un conjunto de datos, una estrategia es:

1. asumir una forma paramétrica para una distribución, como una binomial negativa para la frecuencia o una distribución gamma para la severidad,
2. estimar los parámetros de esa distribución, y luego
3. usar la distribución con los parámetros estimados para calcular la medida de resumen deseada.

Ésta es la aproximación paramétrica. Otra estrategia es estimar la medida de resumen deseada directamente a partir de las observaciones sin referencia a un modelo paramétrico. No es sorprendente que esto se conozca como aproximación no paramétrica Una forma de inferencia que no se basa en una modelo paramétrico.

Comencemos por considerar el tipo más básico de esquema de muestreo y supongamos que las observaciones son realizaciones de un conjunto de variables aleatorias \(X_1, \ldots, X_n\) que son iid independientes e idénticamente distribuidas generadas por una distribución poblacional desconocida \(F(\cdot)\). Un modo equivalente de explicarlo es que \(X_1, \ldots, X_n\), es una muestra aleatoria (con remplazamiento) de \(F(\cdot)\). Para mostrar cómo funciona todo esto, a continuación se describen los estimadores no paramétricos de muchas medidas importantes que resumen una distribución.

4.1.1.1 Estimadores de Momentos

En la Sección 2.2.2 aprendimos como definir momentos para la frecuencia y en la Sección 3.1.1 para la severidad. En particular, el \(k\)-ésimo momento, \(\mathrm{E~}[X^k] = \mu^{\prime}_k\), resume muchos aspectos de la distribución para distintos valores de k. Aquí, \(\mu^{\prime}_k\) es comúnmente denominado el k-ésimo momento poblacional, para distinguirlo del k-ésimo momento muestral, \[ \frac{1}{n} \sum_{i=1}^n X_i^k, \] que es el estimador no paramétrico correspondiente. En las aplicaciones, \(k\) es normalmente un número entero positivo, aunque no es necesario que lo sea.

Un caso particular importante es el primer momento donde k=1. En este caso, el símbolo principal (\(\prime\)) y el subíndice \(1\) generalmente se eliminan y se usa \(\mu=\mu^{\prime}_1\) para denotar la media de la población o, simplemente, la media. El estimador en la muestra correspondiente para \(\mu\) se llama media muestral, denotada con una barra en la parte superior de la variable aleatoria: \[ \bar{X} =\frac{1}{n} \sum_{i=1}^n X_i. \] Otro tipo de medida a modo de resumen que es de interés es el \(k\)-ésimo momento central, \(\mathrm{E~} [(X-\mu)^k] = \mu_k\). Comúnmente, \(\mu^{\prime}_k\) se llama el \(k\)-ésimo momento ordinario para distinguirlo del momento central \(\mu_k\). Un estimador no paramétrico, o muestral, de \(\mu_k\) es \[ \frac{1}{n} \sum_{i=1}^n \left(X_i - \bar{X}\right)^k . \] El segundo momento central (\(k=2\)) es un caso importante para el que generalmente asignamos un nuevo símbolo, \(\sigma^2=\mathrm{E~} [(X-\mu)^2]\), conocido como la varianza. Las propiedades del estimador de momentos muestral de la varianza, \(n^{-1}\sum_{i=1}^n\left (X_i-\bar{X}\right)^2\), se han estudiado ampliamente y por lo tanto es natural que se hayan propuesto muchas variaciones. La variación más utilizada es aquella en la que el tamaño real de la muestra se reduce en uno, por lo que definimos \[ s^2 = \frac{1}{n-1} \sum_{i=1}^n \left(X_i - \bar{X}\right)^2. \] Aquí, el estadístico \(s^2\) se conoce como varianza muestral. Dividir por n-1 en lugar de por n importa poco cuando se dispone de un tamaño de muestra n en miles, como es frecuente en las aplicaciones en seguros. De este modo, el estimador resultante es insesgado, en el sentido de que \(\mathrm{E ~} s^2=\sigma^2\), una propiedad deseable particularmente cuando se interpretan los resultados de un análisis.

4.1.1.2 Función de Distribución Empírica

Hemos visto como calcular los estimadores no paramétricos del momento k-ésimo \(\mathrm{E ~} X^k\). Del mismo modo, para cualquier función conocida \(\mathrm{g}(\cdot)\), podemos estimar \(\mathrm {E ~}\mathrm{g}(X)\) usando \(n^{-1}\sum_{i=1}^n\mathrm{g}(X_i)\).

Ahora supongamos que fijamos un valor de x y consideramos la función \(\mathrm{g}(X)=I(X \le x)\). Aquí, la notación \(I(\cdot)\) es la función del indicador; devuelve 1 si el evento \((\cdot)\) es verdadero y 0 en caso contrario. Para esta elección de \(\mathrm{g}(\cdot)\), el valor esperado es \(\mathrm{E ~}I(X \le x)=\Pr(X \le x)=F(x)\), la función de distribución evaluada en un punto fijo x. Usando el principio analógico, definimos el estimador no paramétrico de la función de distribución \[ \begin{aligned} F_n(x) &= \frac{1}{n} \sum_{i=1}^n I\left(X_i \le x\right) \\ &= \frac{\text{número de observaciones menores o iguales a } x}{n}. \end{aligned} \] Como el estimador no paramétrico \(F_n(\cdot)\) se basa solo en observaciones y no asume una familia paramétrica para la distribución, también se conoce como función de distribución empírica.

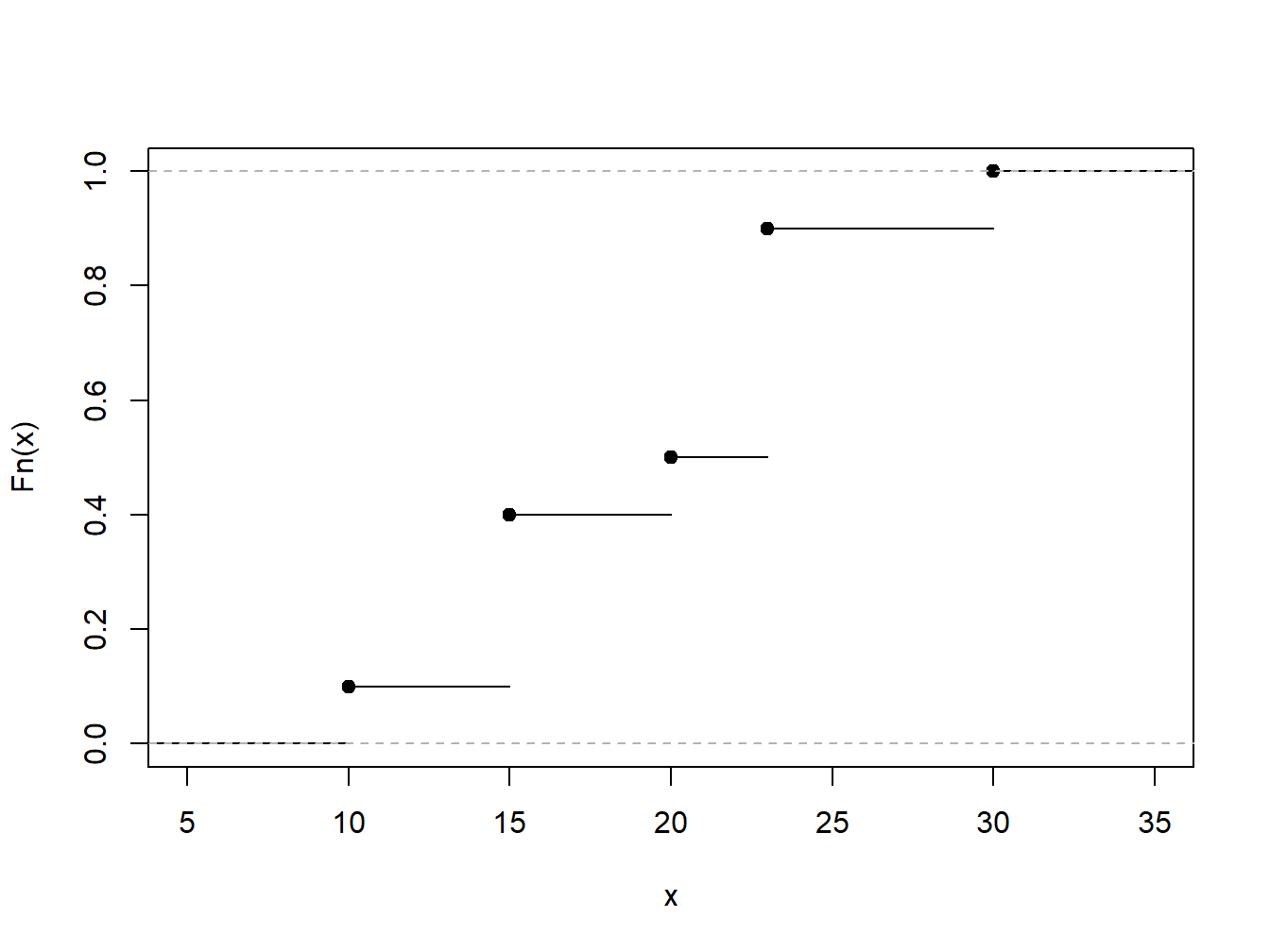
Ejemplo 4.1.1. Conjunto de Datos Ficticios. Como ilustración, considere un conjunto de datos ficticio o “Toy Dataset” de \(n=10\) observaciones. Determinar la función de distribución empírica.

\[ {\small \begin{array}{c|cccccccccc} \hline i &1&2&3&4&5&6&7&8&9&10 \\ X_i& 10 &15 &15 &15 &20 &23 &23 &23 &23 &30\\ \hline \end{array} } \]

Mostrar la Solución del Ejemplo

Debe verificar que la media de la muestra es \(\bar{X}=19,7\) y que la varianza de la muestra es \(s^2=34,45556\). La función de distribución empírica correspondiente es \[ \begin{aligned} F_n(x) &= \left\{ \begin{array}{ll} 0 & \text{ for }\ x<10 \\ 0,1 & \text{ for }\ 10 \leq x<15 \\ 0,4 & \text{ for }\ 15 \leq x<20 \\ 0,5 & \text{ for }\ 20 \leq x<23 \\ 0,9 & \text{ for }\ 23 \leq x<30 \\ 1 & \text{ for }\ x \geq 30, \end{array} \right.\end{aligned} \]

que se muestra en el siguiente gráfico en la Figura 4.1.

Figure 4.1: Función de Distribución Empírica de un Ejemplo con Datos Ficticios

Mostrar código R

(xExample <- c(10,rep(15,3),20,rep(23,4),30))
PercentilesxExample <- ecdf(xExample)
plot(PercentilesxExample, main="",xlab="x")

---

4.1.1.3 Cuartiles, Percentiles y Cuantiles

Anteriormente ya hemos visto la mediana, que es el número tal que aproximadamente la mitad de un conjunto de datos está por debajo (o por encima). El primer cuartil es el número tal que aproximadamente el 25% de los datos está debajo de él y el tercer cuartil es el número tal que aproximadamente el 75% de los datos está debajo de él. Un \(100p\) percentil es el número tal que \(100\times p\) por ciento de los datos están debajo de él.

Para generalizar este concepto, se considera una función de distribución \(F(\cdot)\), que puede o no ser continua, y sea \(q\) una fracción para la cual \(0<q<1\). Queremos definir un cuantil, digamos \(q_F\), para que sea un número tal que \(F(q_F) \approx q\). Observe que cuando \(q=0,5\), \(q_F\) es la mediana; cuando \(q=0,25\), \(q_F\) es el primer cuartil, y así sucesivamente. Por lo tanto, un cuantil generaliza los conceptos de mediana, cuartiles y percentiles.

Para ser precisos, para un determinado valor de \(0<q<1\), se define el \(q\)-ésimo cuantil \(q_F\) como cualquier número que satisfaga \[\begin{equation} F(q_F-) \le q \le F(q_F) \tag{4.1} \end{equation}\]

Aquí, la notación \(F(x-)\) significa evaluar la función \(F(\cdot)\) como el límite por la izquierda.

Para comprender mejor esta definición, veamos algunos casos especiales. Primero, considere el caso en el que \(X\) es una variable aleatoria continua para que la función de distribución \(F(\cdot)\) no tenga puntos de salto, como se ilustra en la Figura 4.2. En esta figura, se muestran algunas fracciones, \(q_1\), \(q_2\) y \(q_3\) con sus cuantiles correspondientes \(q_{F,1}\), \(q_{F,2}\) y \(q_{F,3}\). En cada caso se puede ver que \(F(q_F-)=F(q_F)\), de modo que hay un cuantil único. Al igual que podemos encontrar una inversa de la función de distribución única para cualquier \(0<q<1\), podemos escribir \(q_F=F^{-1}(q)\).

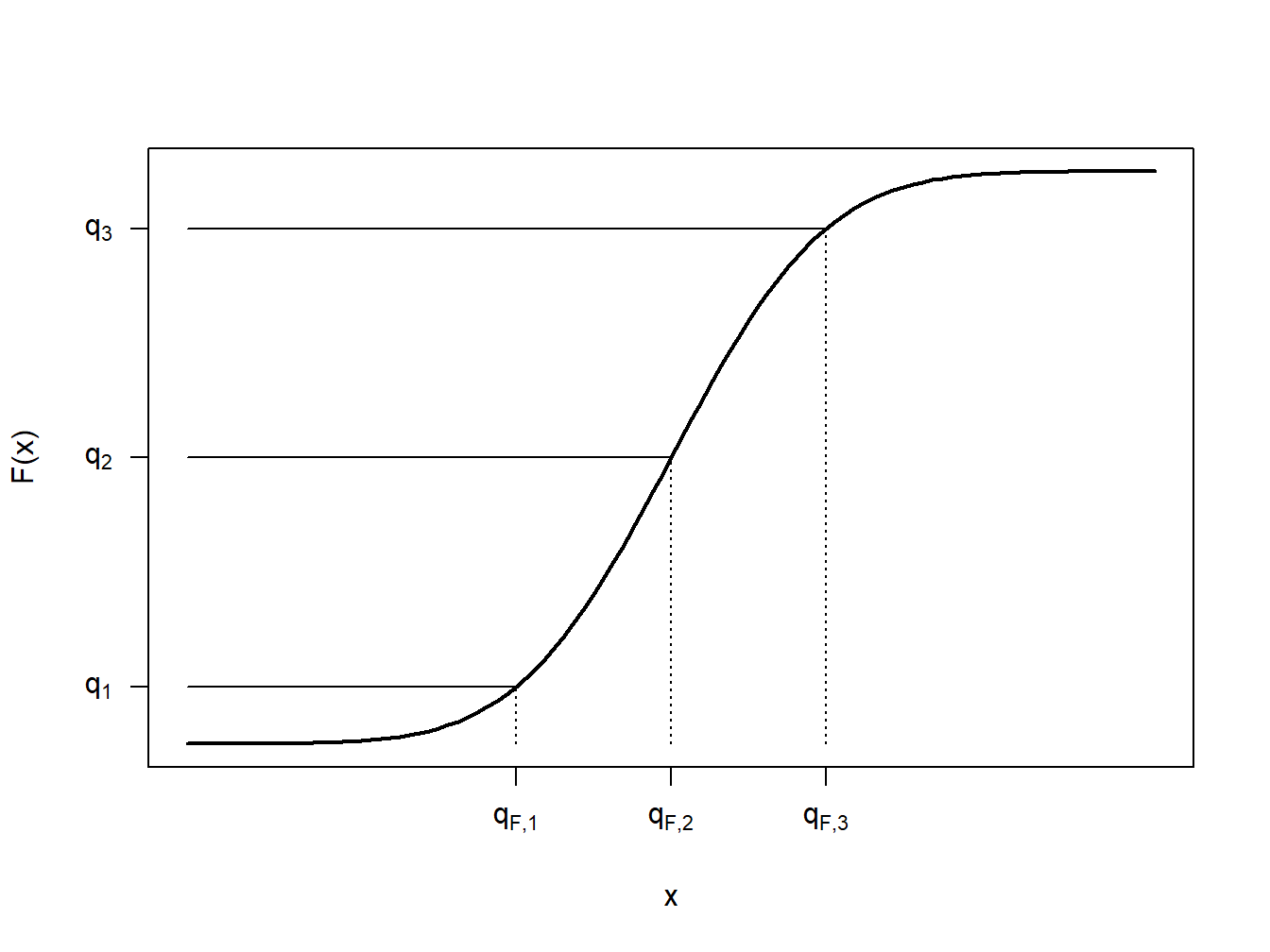
Figure 4.2: Caso de Cuantil Continuo

La figura 4.3 muestra tres casos de funciones de distribución. El panel izquierdo corresponde al caso continuo recién discutido. El panel central muestra un punto de salto similar a los que ya vimos en la función de distribución empírica de la Figura 4.1. Para el valor de \(q\) que se muestra en este panel, todavía tenemos un valor único del cuantil \(q_F\). Aunque hay muchos valores de \(q\) tales que \(F(q_F-) \le q \le F(q_F)\), para un valor particular de \(q\), solo hay una solución para la ecuación (4.1). El panel de la derecha muestra una situación en la que el cuantil no puede determinarse de manera única para el \(q\) que se muestra, ya que hay un rango de \(q_F\) que satisfacen la ecuación (4.1).

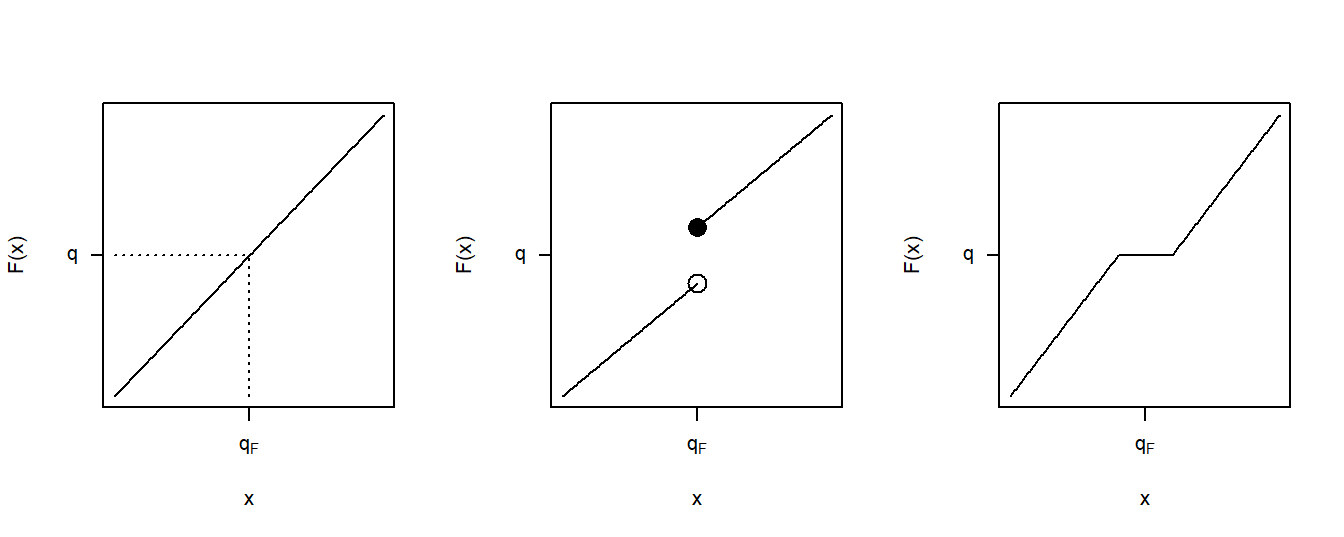
Figure 4.3: Tres Casos de Cuantiles

---

Ejemplo 4.1.2. Conjunto de Datos Ficticios: Continuación. Se determinan los cuantiles correspondientes a los percentiles 20, 50 y 95.

Mostrar la solución del Ejemplo

Solución. Se considera la Figura 4.1. El caso de \(q=0,20\) corresponde al panel central, por lo que el percentil 20 es 15. El caso de \(q=0,50\) corresponde al panel derecho, por lo que la mediana es cualquier número entre 20 y 23, ambos inclusive. Muchos paquetes de software usan el promedio de 21,5 (por ejemplo, R, como se ve a continuación). Para el percentil 95, la solución es 30. Podemos ver en el gráfico que 30 también corresponde a los percentiles 99 y 99,99.

quantile(xExample, probs=c(0.2, 0.5, 0.95), type=6)

##  20%  50%  95% 
## 15.0 21.5 30.0

---

Al tomar un promedio ponderado entre las observaciones de datos, los cuantiles empíricos suavizados pueden asemejarse a los casos como el panel derecho en la Figura 4.3. El \(q\)-ésimo cuartil empírico suavizado se define como \[ \hat{\pi}_q = (1-h) X_{(j)} + h X_{(j+1)} \] donde \(j=\lfloor(n+1)q\rfloor\), \(h=(n+1)q-j\), y \(X_{(1)}, \ldots, X_{(n)}\) son los valores ordenados (conocidos como los estadísticos de orden) correspondientes a \(X_1, \ldots, X_n\). Cabe señalar que \(\hat{\pi}_q\) es simplemente una interpolación lineal entre \(X_{(j)}\) y \(X_{(j+1)}\).

Ejemplo 4.1.3. Conjunto de Datos Ficticios: Continuación. Se determinan los percentiles 50-ésimo y 20-ésimo alisados.

Mostrar la solución del Ejemplo

Solución Se toma \(n=10\) y \(q=0,5\). De modo que, \(j=\lfloor(11)0,5 \rfloor= \lfloor 5,5 \rfloor=5\) y \(h=(11)(0,5)-5=0,5\). Por tanto, el 50-ésimo cuantil empírico alisado es \[\hat{\pi}_{0,5} = (1-0,5) X_{(5)} + (0,5) X_{(6)} = 0,5 (20) + (0,5)(23) = 21,5.\] Ahora se toma \(n=10\) y \(q=0,2\). En este caso, \(j=\lfloor(11)0,2\rfloor=\lfloor 2,2 \rfloor=2\) y \(h=(11)(0,2)-2=0,2\). Entonces, el 20-ésimo cuantil empírico alisado es \[\hat{\pi}_{0,2} = (1-0,2) X_{(2)} + (0,2) X_{(3)} = 0,2 (15) + (0,8)(15) = 15.\]

---

4.1.1.4 Estimadores de la Densidad

Variable Discreta. Cuando la variable aleatoria es discreta, estimar la función de masa de probabilidad \(f(x)=\Pr(X = x)\) es sencillo. Simplemente usamos el promedio del indicador \(I(X_i = x)\) en la muestra, definido como

\[f_n(x) = \frac{1}{n} \sum_{i=1}^n I(X_i = x).\]

Variable Continua Dentro de un Grupo. Para una variable aleatoria continua, se considera una formulación discretizada en la que el dominio de \(F(\cdot)\) está dividido por las constantes \(\{c_0 <c_1 <\cdots <c_k\}\) en intervalos de la forma \([c_{j-1}, c_j)\), por \(j = 1, \ldots, k\). Los datos observados se “agrupan” en función del intervalo en el que caen. Entonces, podríamos usar la definición básica de la función de masa de probabilidad empírica, o una variación como \[f_n(x) = \frac{n_j}{n \times (c_j - c_{j-1})} \ \ \ \ \ \ c_{j-1} \le x < c_j,\] donde \(n_j\) es el número de observaciones (\(X_i\)) que caen en el intervalo \([c_{j-1}, c_j)\).

Variable Continua (no agrupada). Extendiendo esta noción a situaciones en las que observamos datos individuales, se debe tener en cuenta que siempre podemos crear agrupaciones arbitrarias y usar esta fórmula. Más formalmente, dada \(b>0\) una constante positiva que toma un valor reducido y se conoce como ancho de banda (bandwidth), se define el estimador de la densidad como

\[\begin{equation} f_n(x) = \frac{1}{2nb} \sum_{i=1}^n I(x-b < X_i \le x + b) \tag{4.2} \end{equation}\]

Mostrar un fragmento de Teoría

---

La idea es que el estimador \(f_n(x)\) en la ecuación (4.2) es la media sobre \(n\) iid independientes e idénticamente distribuidas realizaciones de una variable aleatoria con media

\[ \begin{aligned} \mathrm{E~ } \frac{1}{2b} I(x-b < X \le x + b) &= \frac{1}{2b}\left(F(x+b)-F(x-b)\right) \\ &= \frac{1}{2b} \left( \left\{ F(x) + b F^{\prime}(x) + b^2 C_1\right\} \left\{ F(x) - b F^{\prime}(x) + b^2 C_2\right\} \right) \\ &= F^{\prime}(x) + b \frac{C_1-C_2}{2} \rightarrow F^{\prime}(x) = f(x), \end{aligned} \]

como \(b \rightarrow 0\). Esto es, \(f_n(x)\) es un estimador asintóticamente insesgado de \(f(x)\) (su esperanza se acerca al valor verdadero a medida que el tamaño de la muestra tiende a infinito). Este desarrollo supone cierta suavización de \(F(\cdot)\), en particular, se deriva dos veces con respecto a \(x\), pero no hace suposiciones sobre la forma de la función de distribución \(F\). Debido a esto, se dice que el estimador de densidad \(f_n\) es no paramétrico.

---

Más generalmente, se define el estimador núcleo (kernel) de la densidad de la función de pdf función de densidad de probabilidad en x como

\[\begin{equation} f_n(x) = \frac{1}{nb} \sum_{i=1}^n w\left(\frac{x-X_i}{b}\right) , \tag{4.3} \end{equation}\]

donde \(w\) es una función de densidad de probabilidad centrada en 0. Se tiene que tener en cuenta que la ecuación (4.2) simplemente se convierte en el estimador núcleo de la densidad donde \(w(x) =\frac{1}{2} I(-1 <x \le 1)\), también conocido como núcleo uniforme. Otras opciones comunes para \(w\) se muestran en Table 4.1.

\[ {\small \begin{matrix} \text{Table 4.1: Opciones más comunes como Núcleo del Estimador de la Densidad}\\ \begin{array}{l|cc} \hline \text{Kernel} & w(x) \\ \hline \text{Uniforme } & \frac{1}{2}I(-1 < x \le 1) \\ \text{Triángulo} & (1-|x|)\times I(|x| \le 1) \\ \text{Epanechnikov} & \frac{3}{4}(1-x^2) \times I(|x| \le 1) \\ \text{Gausiana} & \phi(x) \\ \hline \end{array}\end{matrix} } \]

Siendo \(\phi(\cdot)\) la función de densidad normal estándar. Como veremos en el siguiente ejemplo, la elección del ancho de banda \(b\) viene dada por la existencia de un equilibrio entre sesgo-varianza, es decir, entre las coincidencias con las características locales de la distribución y la reducción de la dispersión.

---

Ejemplo 4.1.4. Fondo Inmobiliario. La figura 4.4 muestra un histograma (con rectángulos grises sombreados) de los logaritmo de los costes de los siniestros en propiedades del año 2010. La curva gruesa (azul) representa la densidad estimada con el núcleo gaussiano, donde el ancho de banda se seleccionó automáticamente utilizando una regla ad-hoc basada en el tamaño de la muestra y la dispersión de los datos. Para este conjunto de datos, el ancho de banda resultó ser \(b = 0,3255\). A modo comparativo, la curva discontinua (roja) representa el estimador de la densidad con un ancho de banda igual a 0,1 y la curva verde, más suave, utiliza un ancho de banda de 1. Como se anticipó, el ancho de banda más pequeño (0,1) implica realizar promedios locales sobre menos datos para obtener una mejor idea del comportamiento local, pero al precio de una mayor dispersión. En contraste, el mayor ancho de banda (1) suaviza las fluctuaciones locales, produciendo una curva más suave que puede perder perturbaciones reales en el promedio local. Para aplicaciones actuariales, utilizamos principalmente el estimador núcleo de la densidad para obtener una impresión visual rápida de los datos. Desde esta perspectiva, simplemente puede usarse la regla ad-hoc predeterminada para la selección del ancho de banda, sabiendo que se tiene la capacidad de cambiarla dependiendo de la situación en cuestión.

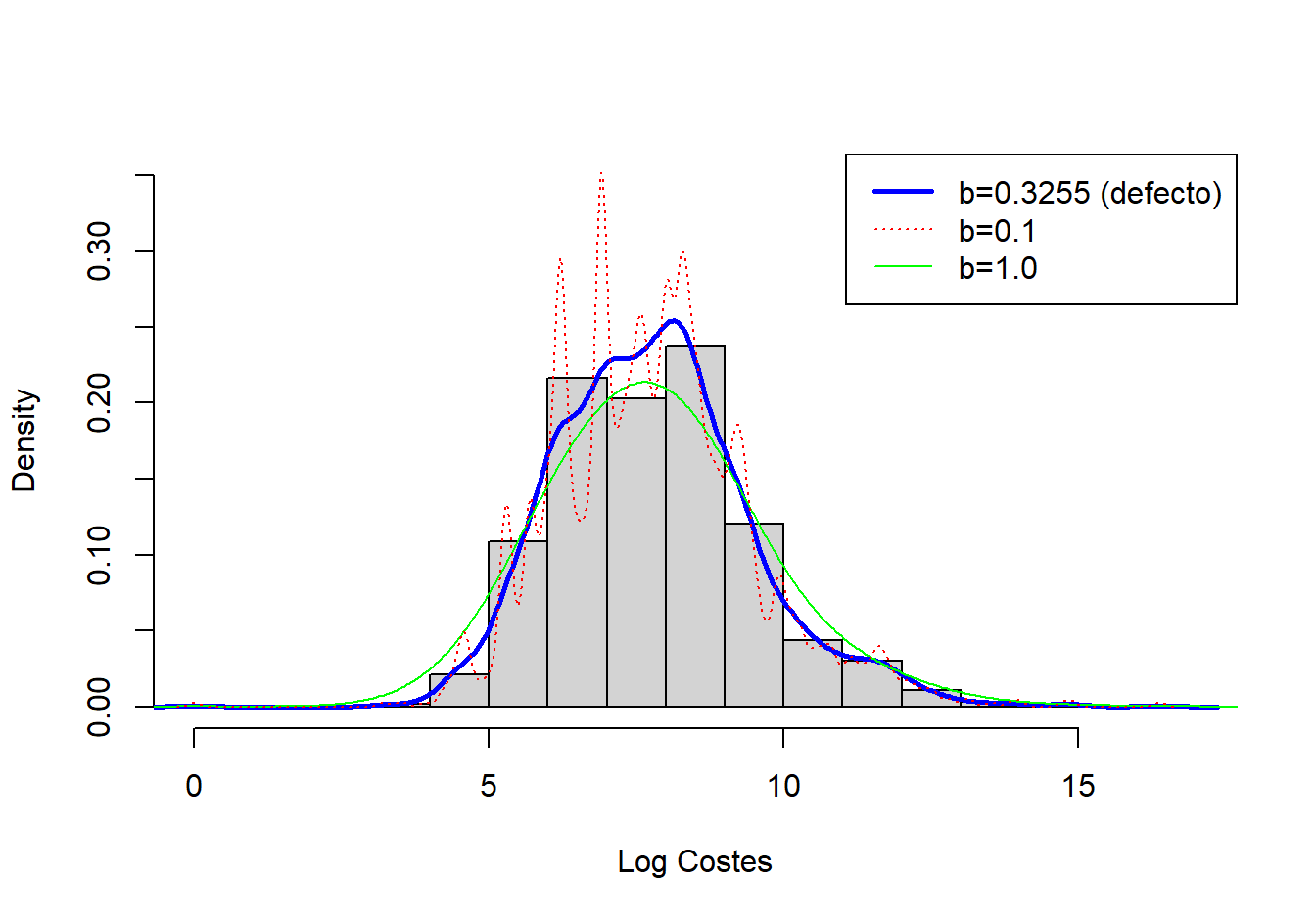
Figure 4.4: Histograma de los Logaritmo de los Costes de los Siniestros en Propiedades con Estimador Núcleo de la Densidad Superpuesto

Mostrar código R

#Comparación de Densidad
hist(log(ClaimData$Claim), main="", ylim=c(0,.35),xlab="Log Costes", freq=FALSE, col="lightgray")
lines(density(log(ClaimData$Claim)), col="blue",lwd=2.5)
lines(density(log(ClaimData$Claim), bw=1), col="green")
lines(density(log(ClaimData$Claim), bw=.1), col="red", lty=3)
legend("topright", c("b=0.3255 (default)", "b=0.1", "b=1.0"), lty=c(1,3,1),
            lwd=c(2.5,1,1), col=c("blue", "red", "green"), cex=1)

---

Los estimadores no paramétricos de la densidad, como el estimador núcleo, se usan habitualmente en la práctica. Este mismo concepto también se puede ampliar para dar versiones suavizadas de una función de distribución empírica. Dada la definición del estimador núcleo de la densidad, el estimador núcleo de la función de distribución se puede obtener como

\[ \begin{aligned} \hat{F}_n(x) = \frac{1}{n} \sum_{i=1}^n W\left(\frac{x-X_i}{b}\right).\end{aligned} \]

donde \(W\) es la función de distribución asociada con la densidad del núcleo \(w\). Para ilustrarlo, para el núcleo uniforme, tenemos \(w(y) = \frac{1}{2}I(-1 < y \le 1)\), de modo que

\[ \begin{aligned} W(y) = \begin{cases} 0 & y<-1\\ \frac{y+1}{2}& -1 \le y < 1 \\ 1 & y \ge 1 \\ \end{cases}\end{aligned} . \]

---

Ejemplo 4.1.5. Pregunta de Examen Actuarial.

Se estudian cinco individuos para estimar el tiempo desde el inicio de una enfermedad hasta la muerte. Los tiempos de muerte son:

\[ \begin{array}{ccccc} 2 & 3 & 3 & 3 & 7 \\ \end{array}. \]

Usando un núcleo triangular con ancho de banda \(2\), calcular la función de densidad estimada en 2,5.

Mostrar la solución del Ejemplo

Solución. Para la estimación núcleo de la densidad tenemos \[f_n(x) = \frac{1}{nb} \sum_{i=1}^n w\left(\frac{x-X_i}{b}\right),\] donde \(n=5\), \(b=2\), y \(x=2,5\). Para un kernel triangular, \(w(x) = (1-|x|)\times I(|x| \le 1)\). Así,

\[ \begin{array}{c|c|c} \hline X_i & \frac{x-X_i}{b} & w\left(\frac{x-X_i}{b} \right) \\ \hline 2 & \frac{2,5-2}{2}=\frac{1}{4} & (1-\frac{1}{4})(1) = \frac{3}{4} \\ \hline 3 & & \\ 3 & \frac{2,5-3}{2}=\frac{-1}{4} & \left(1-\left| \frac{-1}{4} \right| \right)(1) = \frac{3}{4} \\ 3 & & \\ \hline 7 & \frac{2,5-7}{2}=-2,25 & (1-|-2,25|)(0) = 0\\ \hline \end{array} \]

Entonces la estimación núcleo de la densidad es \[f_n(x) = \frac{1}{5(2)}\left( \frac{3}{4} + (3) \frac{3}{4} + 0 \right) = \frac{3}{10}\]

---

4.1.1.5 Principio de Plug-in

Una forma de crear un estimador no paramétrico es usar el principio de analogía o plug-in donde se reemplaza la cdf \(F\) desconocida por un estimador conocido como la cdf empírica \(F_n\). Por tanto, si estamos tratando de estimar \(\mathrm{E}~\mathrm{g}(X)=\mathrm{E}_F~\mathrm{g}(X)\) para una función genérica g, entonces se define un estimador noparamétrico como \(\mathrm{E}_{F_n}~\mathrm{g}(X)=n^{-1}\sum_{i=1}^n\mathrm{g}(X_i)\).

Para ver su funcionamiento, como un caso particular de g consideramos la ratio de eliminación de pérdidas presentada en la Sección 3.4.1, \[LER(d)=\frac{\mathrm{E~}(\min(X,d) )}{\mathrm{E~}(X)}\] para un deducible fijo \(d\).

Ejemplo. 4.1.11. Siniestros con Daños Corporales y Ratio de Eliminación de Pérdidas

Utilizamos una muestra de 432 siniestros cerrados de automóvil ocurridos en Boston de Derrig, Ostaszewski, and Rempala (2001). Las pérdidas se registran para los pagos por daños corporales derivados en los accidentes de automóvil. Las pérdidas no están sujetas a deducibles, pero están sujetas a varios límites de póliza, también disponibles en los datos. Se obtiene que sólo 17 de 432 (\(\approx\) 4%) estaban sujetas al límite en la póliza y, por ello, ignoraremos estos datos en esta ilustración.

La pérdida promedio pagada es 6906. Figura 4.5 muestra otros aspectos de la distribución.

En concreto, el panel izquierdo muestra la función de distribución empírica, el panel derecho proporciona un gráfico de la densidad no paramétrica.

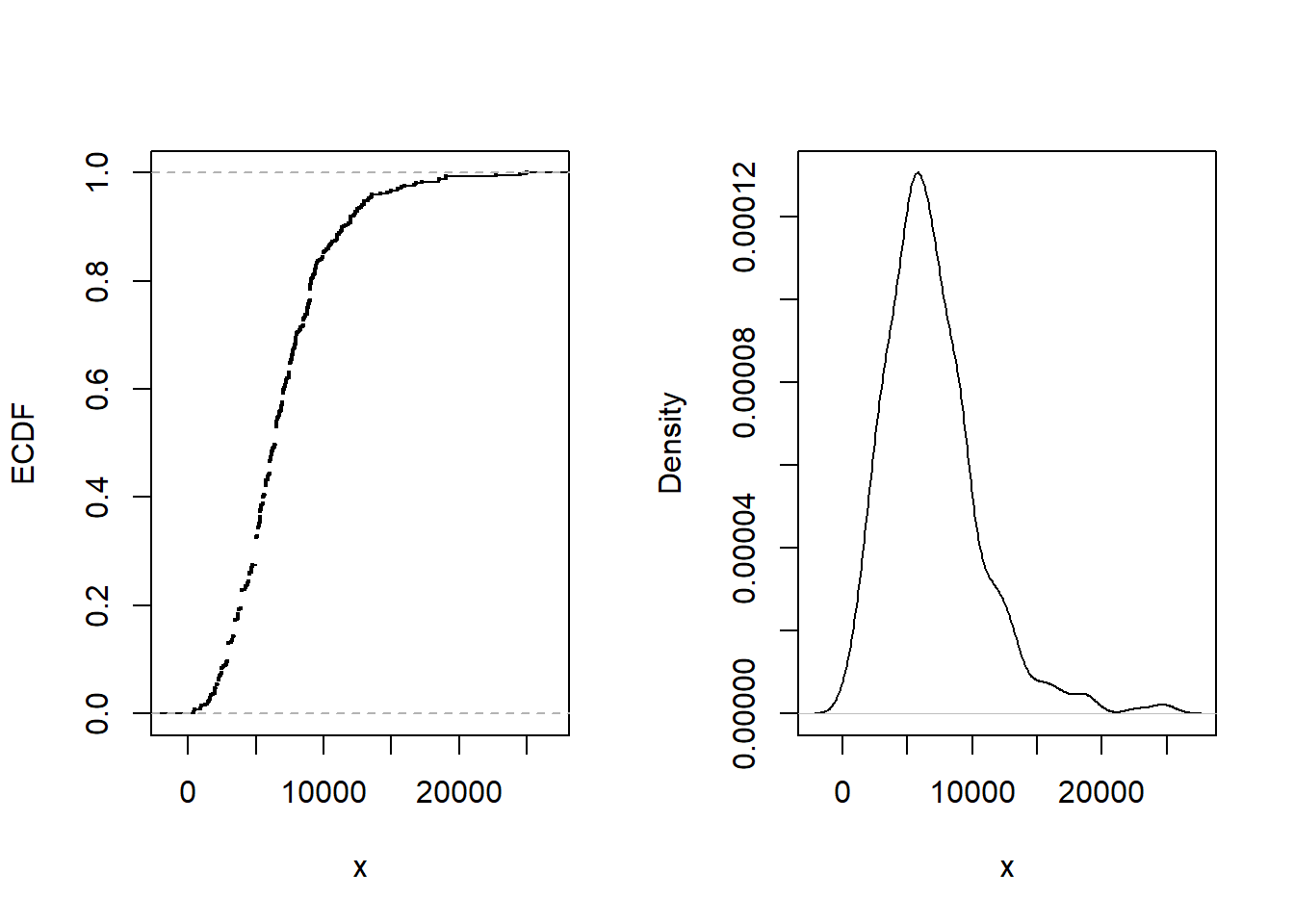
Figure 4.5: Siniestros por daños corporales. La figura de la izquierda proporciona la función de distribución empírica. La figura de la derecha presenta un gráfico de la densidad no paramétrica.

El impacto de las pérdidas por lesiones corporales se puede mitigar mediante la imposición de límites o la compra de pólizas de reaseguro (consulte la Sección 10.3). Para cuantificar el impacto de estas herramientas de mitigación de riesgos, es común calcular el índice de eliminación de pérdida o loss elimination ratio (LER) como se introdujo en la Sección 3.4.1. La función de distribución no está disponible y se debe estimar de alguna manera. Usando el principio plug-in, un estimador no paramétrico se puede definir como \[ LER_n(d) = \frac{n^{-1} \sum_{i=1}^n \min(X_i,d)}{n^{-1} \sum_{i=1}^n X_i} = \frac{\sum_{i=1}^n \min(X_i,d)}{\sum_{i=1}^n X_i} . \]

La figura 4.5 muestra el estimador \(LER_n(d)\) para varias opciones de d. Por ejemplo, si \(d=14.000\), resulta que \(LER_n(14000)\approx\) 0.9768. Imponer un límite de 14.000 significa que esperamos retener 97.68 porcentaje de siniestros.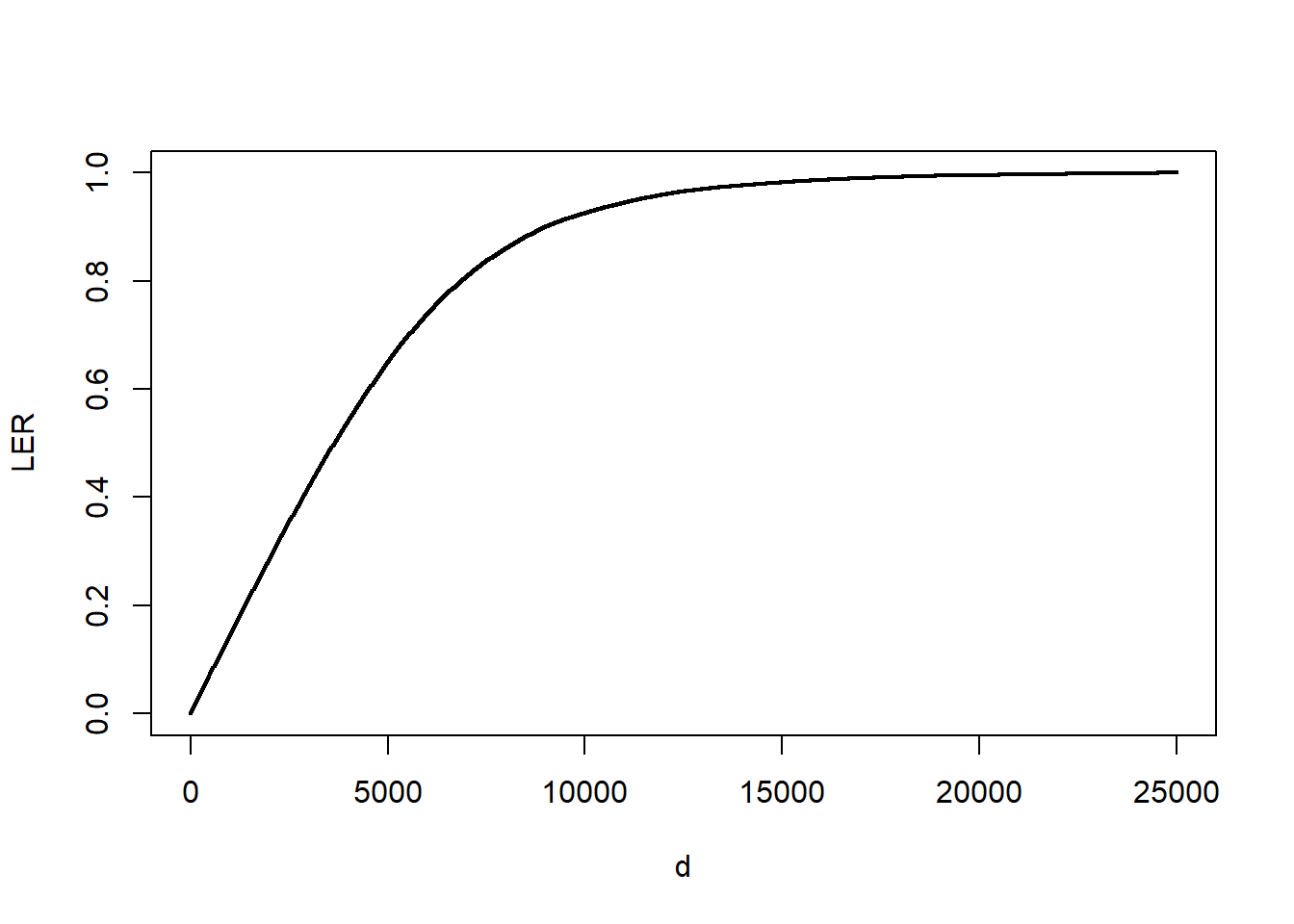

Figure 4.6: LER para siniestros por daños corporales. La figura presenta el índice de eliminación de pérdidas (LER) en función del deducible d.

4.1.2 Herramientas para la Selección de Modelos y Diagnósticos

En la sección anterior se introdujeron estimadores no paramétricos en los que no se asumía una forma paramétrica sobre las distribuciones subyacentes. Sin embargo, en muchas aplicaciones actuariales, los analistas buscan emplear un ajuste paramétrico de una distribución para facilitar la explicación y la capacidad de extenderla fácilmente a situaciones más complejas, como incluir variables explicativas en un entorno de regresión. Al ajustar una distribución paramétrica, un analista podría intentar usar una distribución gamma para representar un conjunto de datos de pérdida. Sin embargo, otro analista podría preferir usar una distribución de Pareto. ¿Cómo se sabe qué modelo seleccionar?

Se pueden utilizar herramientas no paramétricas para corroborar la selección de modelos paramétricos. Esencialmente, el enfoque es calcular las medidas de resumen seleccionadas bajo un modelo paramétrico ajustado y compararlo con el valor correspondiente bajo el modelo no paramétrico. Como el no paramétrico no asume una distribución específica y es simplemente una función de los datos, se utiliza como punto de referencia para evaluar cómo de bien la distribución/modelo paramétrico representa los datos. Esta comparación puede alertar al analista de deficiencias en el modelo paramétrico y, a veces, señalar formas de mejorar la especificación paramétrica. Los procedimientos orientados a evaluar la validez de un modelo se conocen como diagnóstico del modelo.

4.1.2.1 Comparación Gráfica de Distribuciones

Ya hemos visto la técnica de superponer gráficos para fines de comparación. Para reforzar la aplicación de esta técnica, la Figura @ref(fig: ComparisonCDFPDF) compara la distribución empírica con dos distribuciones paramétricas ajustadas. El gráfico izquierdo muestra las funciones de distribución de las distribuciones de siniestros. Los puntos que forman una curva “en forma de S” representan la función de distribución empírica en cada observación. La curva azul gruesa proporciona los valores correspondientes para la distribución gamma ajustada y el púrpura claro corresponde a la distribución de Pareto ajustada. Como la distribución de Pareto está mucho más cerca de la función de distribución empírica que la de la gamma, esto nos proporciona una evidencia de que la Pareto es el mejor modelo para este conjunto de datos. El gráfico derecho ofrece información similar para la función de densidad y proporciona un mensaje coherente. Basado (sólo) en estos gráficos, la distribución de Pareto es la opción preferida para el analista.

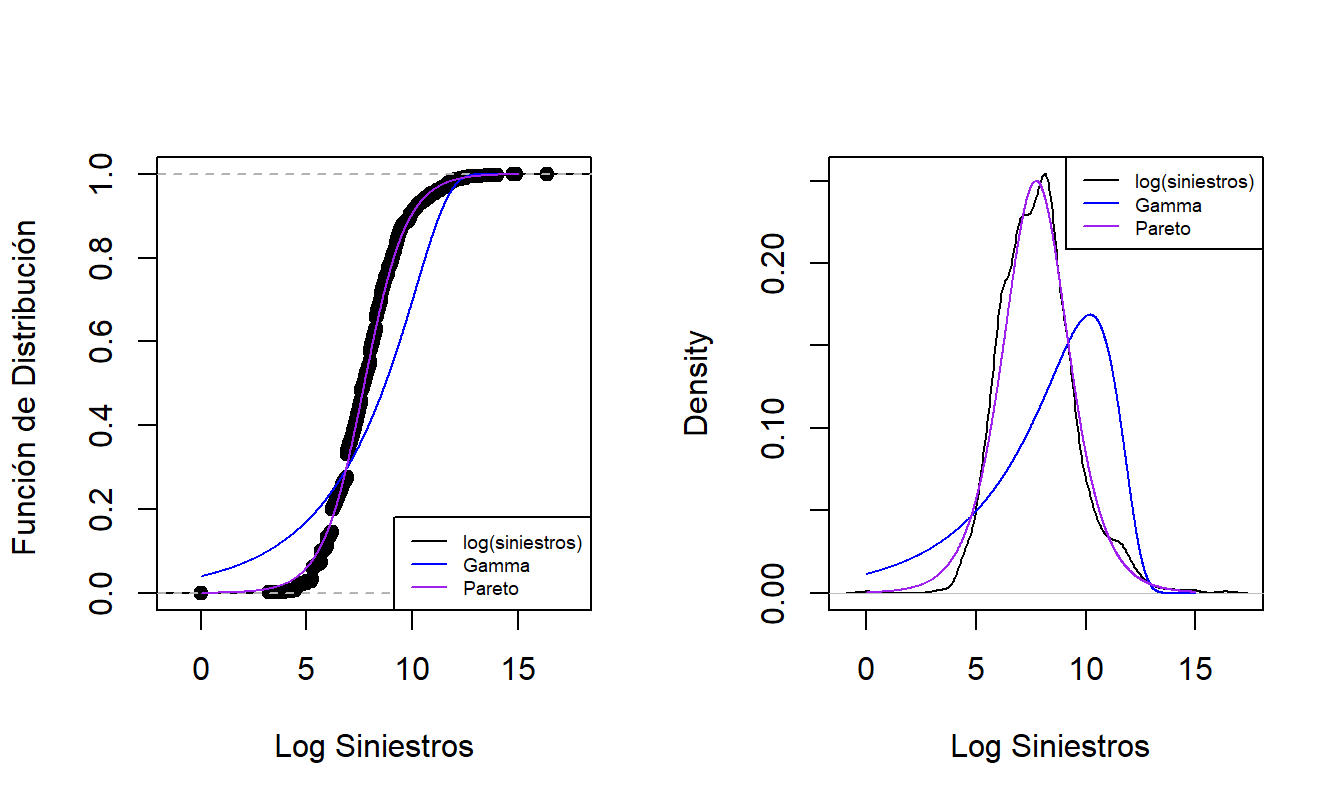
Figure 4.7: Distribución paramétrica versus paramétrica ajustada y funciones de densidad. El gráfico de la izquierda compara las funciones de distribución, con los puntos correspondientes a la distribución empírica, la curva azul gruesa correspondiente a la gamma ajustada y la curva de color púrpura claro correspondiente al Pareto ajustado. El gráfico de la derecha compara estas tres distribuciones resumidas usando funciones de densidad de probabilidad.

Otra forma de comparar la idoneidad de dos modelos ajustados es a partir del gráfico de probabilidad-probabilidad (\(pp\)). Un gráfico \(pp\) compara las probabilidades acumuladas en dos modelos. Para nuestro propósito, estos dos modelos son la función de distribución empírica no paramétrica y el modelo paramétrico ajustado. La Figura @ref(fig: PPPlot) muestra los gráficos \(pp\) para los datos del Fondo de la Propiedad. La gamma ajustada está a la izquierda y la Pareto ajustada está a la derecha, en comparación con la misma función de distribución empírica de los datos. La línea recta representa la igualdad entre las dos distribuciones que se comparan, por lo que son deseables los puntos cercanos a la línea. Como se vio en demostraciones anteriores, la Pareto está mucho más cerca de la distribución empírica que la gamma, lo que proporciona evidencia adicional de que la Pareto es el mejor modelo.

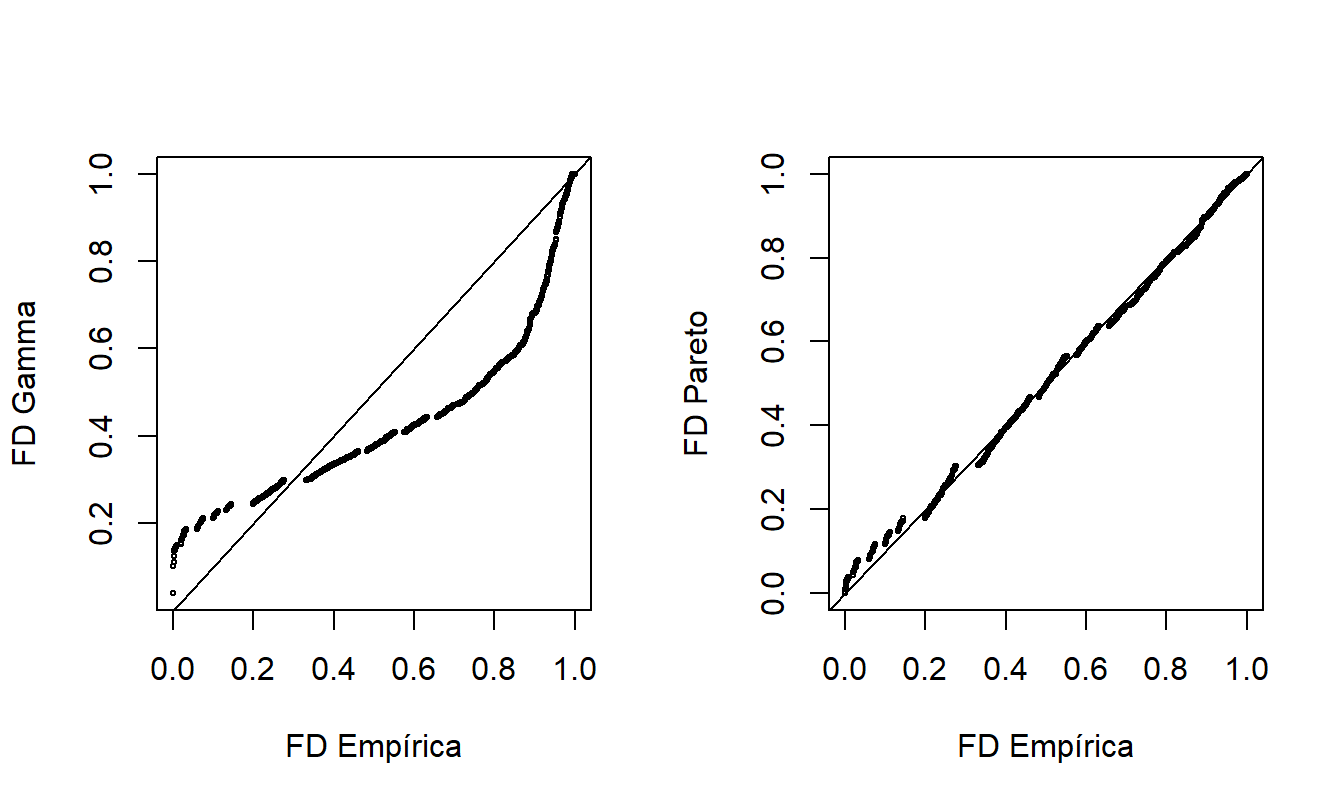
Figure 4.8: Gráficos de Probabilidad-Probabilidad (\(pp\)). Los ejes horizontales representan la función de distribución empírica en cada observación. En el gráfico izquierdo, la función de distribución correspondiente a la gamma se muestra en el eje vertical. El gráfico de la derecha muestra la distribución de Pareto ajustada. Las líneas de \(y=x\) se superponen.

Un gráfico \(pp\) es útil en parte porque no se requiere escala artificial, como con la superposición de densidades en la Figura @ref(fig: ComparisonCDFPDF), en la que cambiamos a la escala logarítmica para visualizar mejor los datos. El Capítulo 4 Suplemento técnico A.1 introduce una variación del diagrama \(pp\) conocido como curva de Lorenz; Ésta es una herramienta importante para evaluar la desigualdad de ingresos. Además, los gráficos \(pp\) están disponibles en entornos multivariantes en los que hay más de una variable disponible. Sin embargo, una limitación del gráfico \(pp\) es que, debido a que es un gráfico de funciones de distribución acumulativas, a veces puede resultar difícil detectar dónde una distribución paramétrica ajustada es deficiente. Como alternativa, se usa frecuentemente un gráfico cuantil-cuantil (\(qq\)), como se muestra en la Figura 4.9.

El gráfico \(qq\) compara dos modelos ajustados a través de sus cuantiles. Al igual que con los gráficos \(pp\), comparamos el modelo no paramétrico con un modelo ajustado paramétrico. Los cuantiles se pueden evaluar en cada punto del conjunto de datos o en una cuadrícula (por ejemplo, en \(0, 0,001, 0,002, \ldots, 0,999, 1.000\)), dependiendo de la aplicación. En la Figura 4.9, para cada punto en la cuadrícula mencionada, el eje horizontal muestra el cuantil empírico y el eje vertical muestra el correspondiente cuantil paramétrico ajustado (gamma para los dos gráficos superiores, Pareto para los dos inferiores). Los cuantiles se trazan en la escala original en los gráficos izquierdos y en la escala logarítmica en los gráficos derechos para permitirnos ver dónde una distribución ajustada es deficiente. La línea recta representa la igualdad entre la distribución empírica y la distribución ajustada. A partir de estos gráficos, nuevamente vemos que en general la Pareto se ajusta mejor que la gamma. Además, el gráfico inferior derecho sugiere que la distribución de Pareto muestra un buen ajuste con valores grandes, pero proporciona un peor ajuste para valores pequeños.

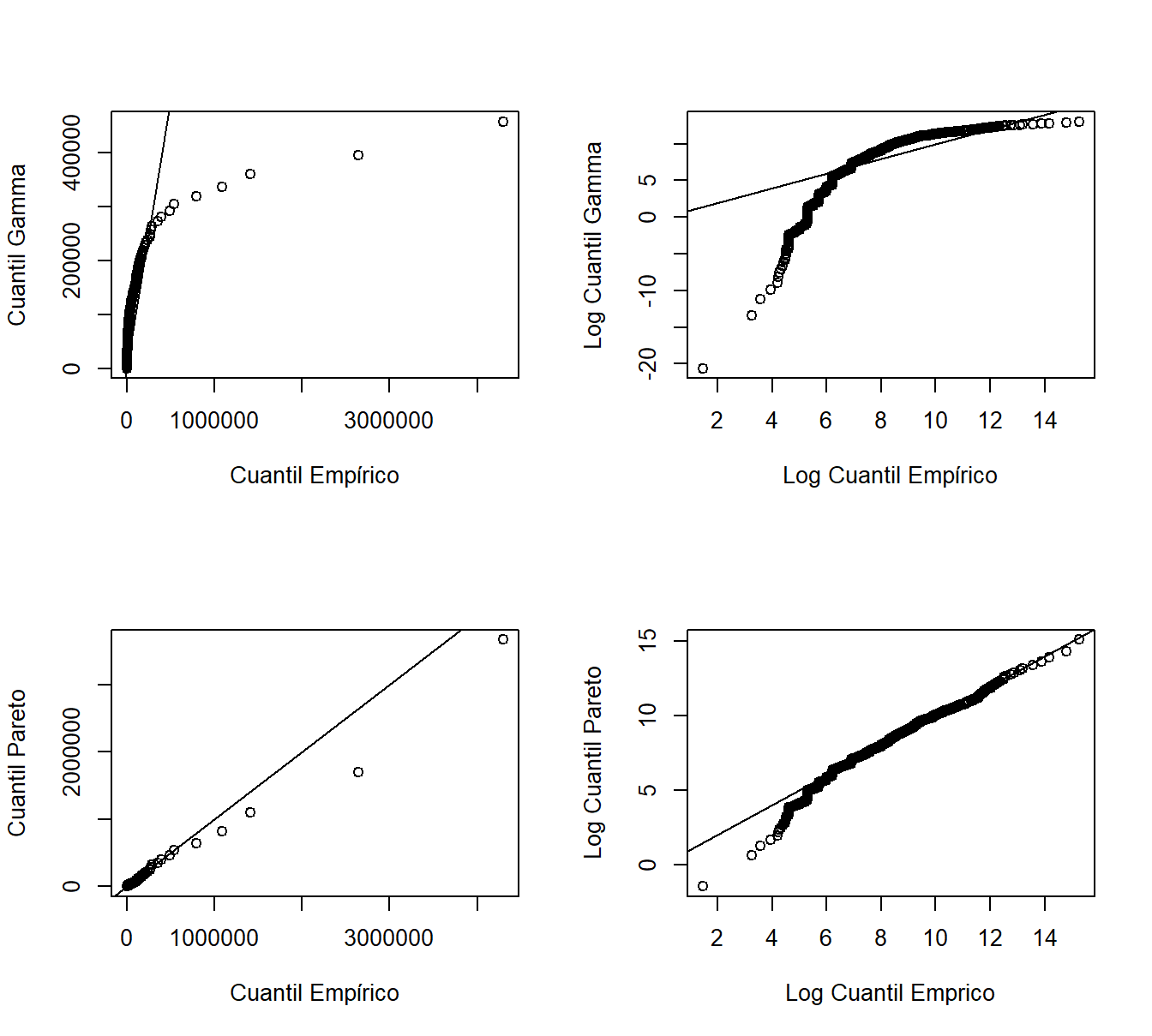
Figure 4.9: Gráficos Cuantil-Cuantil (\(qq\)). Los ejes horizontales representan los cuantiles empíricos en cada observación. Los gráficos de la derecha están representados sobre una base logarítmica. El eje vertical contiene los cuantiles de las distribuciones ajustadas; los cuantiles gamma están en los gráficos superiores, los cuantiles de Pareto están en los gráficos inferiores.

---

Ejemplo 4.1.6. Pregunta de Examen Actuarial. La siguiente figura muestra un gráfico \(pp\) de una distribución ajustada en comparación con una muestra.

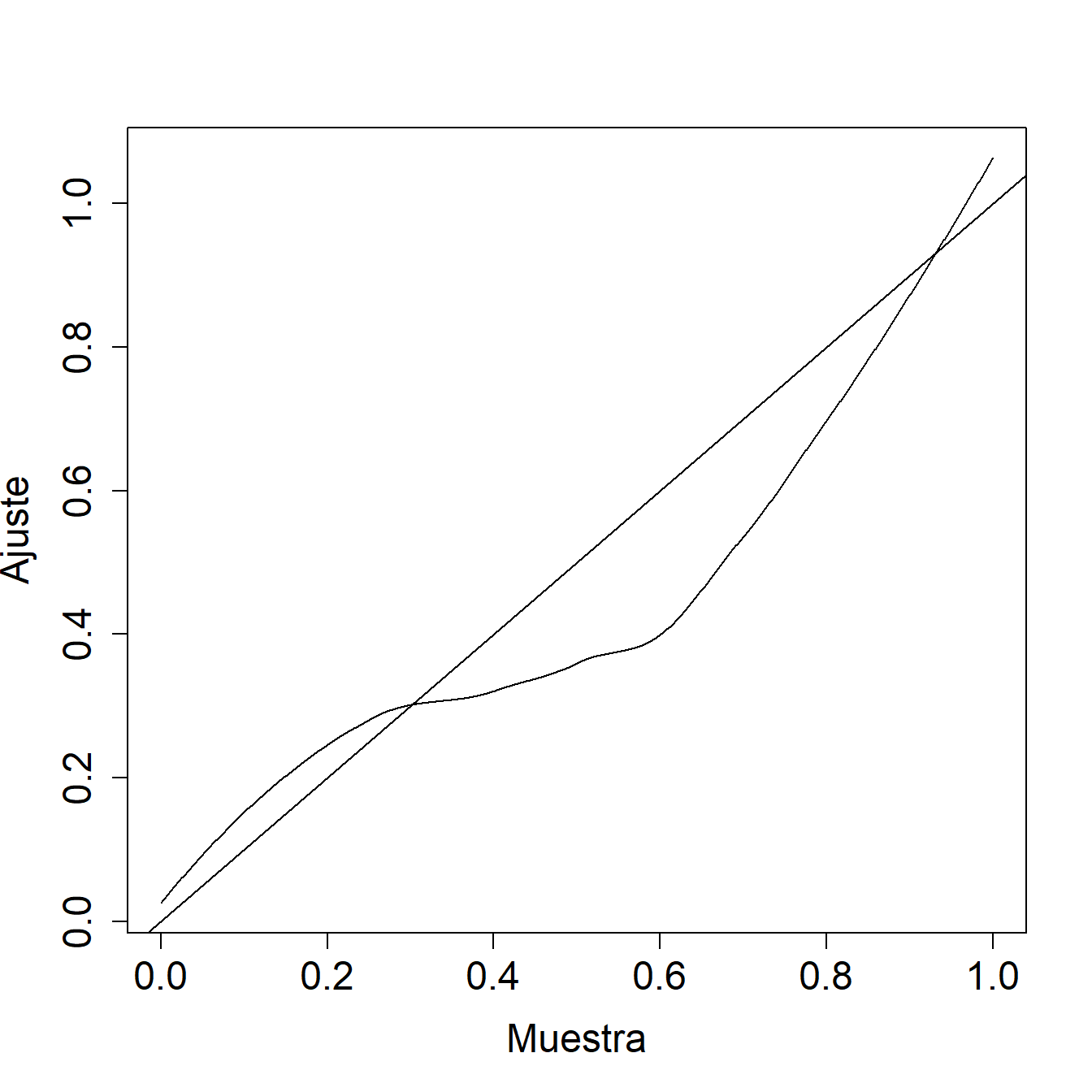
Comente las dos distribuciones con respecto a la cola izquierda, la cola derecha y las probabilidades medianas.

Mostrar la solución del ejemplo

Solución. La cola de la distribución ajustada es demasiado gruesa a la izquierda, demasiado delgada a la derecha, y la distribución ajustada tiene menos probabilidad alrededor de la mediana que la muestra. Para ver esto, recuerde que el gráfico \(pp\) representa gráficamente la distribución acumulada de dos distribuciones en sus ejes (empírica en el eje \(x\) y ajustada en el eje \(y\) en este caso). Para valores pequeños de \(x\), el modelo ajustado asigna una mayor probabilidad de estar por debajo de ese valor que el que se produjo en la muestra (es decir, \(F(x)>F_n(x)\)). Esto indica que el modelo tiene una cola izquierda más pesada que los datos. Para valores grandes de \(x\), el modelo nuevamente asigna una mayor probabilidad de estar por debajo de ese valor y, por lo tanto, menos probabilidad de estar por encima de ese valor (es decir, \(S(x)<S_n(x)\). Esto indica que el modelo tiene una cola derecha más fina que los datos. Además, a medida que avanzamos de 0,4 a 0,6 en el eje horizontal (mirando así el 20% medio de los datos), el gráfico \(pp\) aumenta aproximadamente de 0,3 a 0,4. Esto indica que el modelo asigna sólo alrededor del 10% de la probabilidad en este rango.

---

4.1.2.2 Comparación Estadística de Distribuciones

Para seleccionar un modelo es útil realizar las representaciones gráficas previas. Sin embargo, para mostrar los resultados, puede ser necesario complementar los gráficos con estadísticos de selección que resumen la bondad de ajuste del modelo. La Tabla 4.2 proporciona tres estadísticos de bondad de ajuste de uso frecuente. En esta tabla, \(F_n\) es la distribución empírica, \(F\) es la distribución ajustada o hipotética, y \(F_i=F(x_i)\).

\[ {\small \begin{matrix} \text{Tabla 4.2: Tres Estadísticos de Bondad de Ajuste } \\ \begin{array}{l|cc} \hline \text{Estadístico} & \text{Definición} & \text{Expresión Computacional} \\ \hline \text{Kolmogorov-} & \max_x |F_n(x) - F(x)| & \max(D^+, D^-) \text{ donde} \\ ~~~\text{Smirnov} && D^+ = \max_{i=1, \ldots, n} \left|\frac{i}{n} - F_i\right| \\ && D^- = \max_{i=1, \ldots, n} \left| F_i - \frac{i-1}{n} \right| \\ \text{Cramer-von Mises} & n \int (F_n(x) - F(x))^2 f(x) dx & \frac{1}{12n} + \sum_{i=1}^n \left(F_i - (2i-1)/n\right)^2 \\ \text{Anderson-Darling} & n \int \frac{(F_n(x) - F(x))^2}{F(x)(1-F(x))} f(x) dx & -n-\frac{1}{n} \sum_{i=1}^n (2i-1) \log\left(F_i(1-F_{n+1-i})\right)^2 \\ \hline \end{array} \\ \end{matrix} } \]

El estadístico de Kolmogorov-Smirnov es igual a la diferencia absoluta máxima entre la función de distribución ajustada y la función de distribución empírica. En lugar de comparar diferencias entre puntos individuales, el estadístico de Cramer-von Mises integra la diferencia entre las funciones de distribución empíricas y ajustadas en todo el rango de valores. El estadístico de Anderson-Darling también integra esta diferencia en el rango de valores, aunque ponderada por la inversa de la varianza. Por lo tanto, pone mayor énfasis en las colas de la distribución (es decir, cuando \(F(x)\) o \(1-F(x)=S(x)\) es pequeño).

---

Ejemplo 4.1.7. Pregunta de Examen Actuarial (modificada). Una muestra de pagos de siniestros es:

\[ \begin{array}{ccccc} 29 & 64 & 90 & 135 & 182 \\ \end{array} \]

Comparar la distribución empírica de siniestros con una distribución exponencial con una media de \(100\) calculando el valor del estadístico de prueba de Kolmogorov-Smirnov.

Mostrar solución del ejemplo

Solución. Para una distribución exponencial con una media de \(100\), la función de distribución acumulada es \(F(x)=1-e^{-x/100}\). Así, \[ \begin{array}{ccccc} \hline x & F(x) & F_n(x) & F_n(x-) & \max(|F(x)-F_n(x)|,|F(x)-F_n(x-)|) \\ \hline 29 & 0,2517 & 0,2 & 0 & \max(0,0517, 0,2517) = 0,2517 \\ 64 & 0,4727 & 0,4 & 0,2 & \max(0,0727, 0,2727) = 0,2727 \\ 90 & 0,5934 & 0,6 & 0,4 & \max(0,0066, 0,1934) = 0,1934 \\ 135 & 0,7408 & 0,8 & 0,6 & \max(0,0592, 0,1408) = 0,1408 \\ 182 & 0,8380 & 1 & 0,8 & \max(0,1620, 0,0380) = 0,1620 \\ \hline \end{array} \]

El estadístico de la prueba de Kolmogorov-Smirnov es, por lo tanto, \(KS = \max(0,2517, 0,2727, 0,1934, 0,1408, 0,1620) = 0,2727\).

---

4.1.3 Valores Iniciales

Los métodos de momentos y basados en la coincidencia de percentiles son métodos de estimación no paramétricos que proporcionan alternativas a la máxima verosimilitud. Generalmente, la máxima verosimilitud es la técnica preferida porque emplea los datos de manera más eficiente. (Consulte el Capítulo 17 del Apéndice para obtener las definiciones precisas de eficiencia). Sin embargo, los métodos de momentos y coincidencia de percentiles son útiles porque son más fáciles de interpretar y, por lo tanto, permiten que el actuario o el analista explique los procedimientos a terceros. Además, el procedimiento de estimación numérica (por ejemplo, si se realiza en ‘R’) para la máxima verosimilitud es iterativo y requiere valores iniciales para comenzar el proceso recursivo. Aunque muchos problemas son robustos ante la elección de los valores iniciales, en algunas situaciones complejas, puede ser importante tener un valor inicial cercano al valor óptimo (desconocido). El método de los momentos y la coincidencia de percentiles son técnicas que pueden producir estimaciones deseables sin un elevado coste en términos computacionales y, por lo tanto, pueden usarse como un valor inicial para estimar los parámetros por máxima verosimilitud.

4.1.3.1 Método de Momentos

Con el método de momentos, aproximamos los momentos de la distribución paramétrica utilizando los momentos empíricos (no paramétricos) descritos en la Sección 4.1.1.1. Entonces podemos obtener algebraicamente las estimaciones de los parámetros. ***

Ejemplo 4.1.8. Fondo de Propiedad. Para el fondo inmobiliario de 2010, hay \(n=1.377\) siniestros individuales (en miles de dólares) con

\[m_1 = \frac{1}{n} \sum_{i=1}^n X_i = 26,62259 \ \ \ \ \text{y} \ \ \ \ m_2 = \frac{1}{n} \sum_{i=1}^n X_i^2 = 136.154,6 .\]

Ajustar los parámetros de las distribuciones gamma y Pareto utilizando el método de los momentos.

Mostrar solución del ejemplo

Solución.

Para ajustar una distribución gamma, tenemos \(\mu_1=\alpha\theta\) y \(\mu_2^{\prime}=\alpha(\alpha+1)\theta^2\). Al resolver ambas ecuaciones para obtener la estimación por el método de los momentos, mediante cálculos sencillos se muestra que

\[\alpha = \frac{\mu_1^2}{\mu_2^{\prime}-\mu_1^2} \ \ \ \text{y} \ \ \ \theta = \frac{\mu_2^{\prime}-\mu_1^2}{\mu_1}.\]

Por lo tanto, los estimadores por el método de los momentos son \[ \begin{aligned} \hat{\alpha} &= \frac{26,62259^2}{136154,6-26,62259^2} = 0,005232809 \\ \hat{\theta} &= \frac{136154,6-26,62259^2}{26,62259} = 5.087,629. \end{aligned} \]

A modo de comparación, los valores obtenidos por máxima verosimilitud son \(\hat{\alpha}_{MLE}=0,2905959\) y \(\hat{\theta}_{MLE}=91,61378\), por lo que hay grandes discrepancias entre las estimaciones obtenidas con los dos procedimientos. Esto es una indicación, como hemos visto antes, de que el modelo gamma no se ajusta bien.

En contraste, ahora se asume una distribución de Pareto, de modo que \(\mu_1 = \theta/(\alpha -1)\) y \(\mu_2^{\prime} = 2\theta^2/((\alpha-1)(\alpha-2) )\). mediante cálculos sencillos se muestra que

\[\alpha = 1+ \frac{\mu_2^{\prime}}{\mu_2^{\prime}-\mu_1^2} \ \ \ \ \text{and} \ \ \ \ \ \theta = (\alpha-1)\mu_1.\]

Por lo tanto, los estimadores por el método de los momentos son \[ \begin{aligned} \hat{\alpha} &= 1+ \frac{136154,6}{136154,6-26,62259^2} = 2,005233 \\ \hat{\theta} &= (2,005233-1) \cdot 26,62259 = 26,7619 \end{aligned} \]

Los valores estimados por máxima verosimilitud son \(\hat{\alpha}_{MLE}=0,9990936\) y \(\hat{\theta}_{MLE}=2,2821147\). Es interesante que \(\hat{\alpha}_{MLE}<1\); para la distribución de Pareto, recuerde que \(\alpha<1\) significa que la media es infinita. Esto es otro indicio de que el conjunto de datos de siniestros de la propiedad tiene una distribución de cola larga y pesada.

---

Como se sugiere en el ejemplo anterior, existe flexibilidad con el método de los momentos. Por ejemplo, podríamos haber igualado el segundo y el tercer momento en lugar del primero y el segundo, obteniendo diferentes estimadores. Además, no hay garantía de que exista una solución para cada problema. Adicionalmente, con datos censurados o truncados, hacer coincidir los momentos es solo posible para algunos problemas, y en general, es un escenario más complejo. Finalmente, para distribuciones donde los momentos no existen o son infinitos, el método de momentos no se puede aplicar. Como alternativa, se puede usar la técnica de coincidencia de percentiles.

4.1.3.2 Coincidencia de percentiles

Bajo el método de coincidencia de percentiles, aproximamos los cuantiles o percentiles de la distribución paramétrica utilizando los cuantiles o percentiles empíricos (no paramétricos) descritos en la Sección 4.1.1.3.

---

Ejemplo 4.1.9. Fondo de propiedad.

Para el fondo inmobiliario de 2010, ilustramos la correspondencia en cuantiles. En concreto, la distribución de Pareto es intuitivamente sencilla debido a la expresión cerrada para los cuantiles. Recuerde que la función de distribución para la distribución de Pareto es

\[F(x) = 1 - \left(\frac{\theta}{x+\theta}\right)^{\alpha}.\] Mediante sencillos cálculos se muestra que podemos expresar el cuantil como

\[F^{-1}(q) = \theta \left( (1-q)^{-1/\alpha} -1 \right).\] for a fraction \(q\), \(0<q<1\).

Determinar las estimaciones de los parámetros de la distribución de Pareto utilizando los cuantiles empíricos 25 y 95.

Mostrar solución del ejemplo

Solución.

El percentil 25 (el primer cuartil) es \(0,78853\) y el percentil 95 es \(50,98293\) (ambos en miles de dólares). Con dos ecuaciones

\[0,78853 = \theta \left( 1- (1-0,25)^{-1/\alpha} \right) \ \ \ \ \text{y} \ \ \ \ 50,98293 = \theta \left( 1- (1-0,95)^{-1/\alpha} \right)\] y dos incógnitas, la solución es \[\hat{\alpha} = 0,9412076 \ \ \ \ \ \text{y} \ \ \ \ \hat{\theta} = 2,205617 .\] Observamos aquí que se requiere una rutina numérica para estas soluciones ya que no hay una solución analítica disponible. Además, recuerde que las estimaciones de máxima verosimilitud son \(\hat{\alpha}_{MLE}=0,9990936\) y \(\hat{\theta}_{MLE} = 2,2821147\), por lo que la coincidencia de percentiles proporciona una mejor aproximación para la distribución de Pareto que el método de los momentos.

---

Ejemplo 4.1.10. Pregunta de Examen Actuarial.

Te dan:

1. Las pérdidas siguen una distribución loglogística con función de distribución acumulada: \[F(x) = \frac{\left(x/\theta\right)^{\gamma}}{1+\left(x/\theta\right)^{\gamma}}\]
2. La muestra de pérdidas es:

\[ \begin{array}{ccccccccccc} 10 &35 &80 &86 &90 &120 &158 &180 &200 &210 &1500 \\ \end{array} \]

Estimar \(\theta\) mediante la coincidencia de percentiles, utilizando las estimaciones de percentiles empíricos suavizados del 40 y 80.

Mostrar solución del ejemplo

Solución. Con 11 observaciones, tenemos \(j=\lfloor(n+1)q\rfloor = \lfloor 12(0,4) \rfloor = \lfloor 4,8\rfloor=4\) y \(h=(n+1)q-j = 12(0,4)-4=0,8\). Por interpolación, la estimación del percentil 40 empírico suavizado es \(\hat{\pi}_{0,4} = (1-h) X_{(j)} + h X_{(j+1)} = 0,2(86)+0,8(90)=89,2\).

Del mismo modo, para la estimación del percentil 80 empírico suavizado, tenemos \(12(0,8)=9,6\) entonces la estimación es \(\hat{\pi}_{0,8} = 0,4(200)+0,6(210)=206\).

Usando la distribución acumulada loglogística, necesitamos resolver las siguientes dos ecuaciones para los parámetros \(\theta\) y \(\gamma\): \[0,4=\frac{(89,2/\theta)^\gamma}{1+(89,2/\theta)^\gamma} \ \ \ \text{y} \ \ \ \ 0,8=\frac{(206/\theta)^\gamma}{1+(206+\theta)^\gamma}\]

Resolviendo para cada expresión entre paréntesis da \(\frac{2}{3}=(89,2/\theta)^\gamma\) y \(4=(206/\theta)^\gamma\). Sustituyendo la razón de la segunda ecuación en la primera da \(6=(206/89,2)^\gamma \Rightarrow \gamma=\frac{\ln(6)}{\ln(206/89,2)} = 2,1407\). Entonces \(4^{1/2,1407}=206/\theta \Rightarrow \theta=107,8\)

---

Al igual que el método de los momentos, la coincidencia de percentiles es también muy sensible en el sentido de que muchos estimadores pueden basarse en coincidencias de percentiles; por ejemplo, un actuario puede basar la estimación en los percentiles 25 y 95, mientras que otro actuario utiliza los percentiles 20 y 80. En general, estos estimadores serán diferentes y no hay una razón convincente para preferir uno sobre el otro. Por otro lado, como con el método de los momentos, la coincidencia de percentiles es atractiva porque proporciona una técnica que se puede aplicar fácilmente en distintas situaciones y tiene una base intuitiva. Aunque la mayoría de las aplicaciones actuariales usan estimadores de máxima verosimilitud, puede ser conveniente utilizar enfoques alternativos como el método de momentos y la coincidencia de percentiles.

4.2 Selección del Modelo

---

En esta sección, se aprende a:

• Describir el proceso iterativo de especificación y de selección de modelo.
• Esquematizar los pasos necesarios para seleccionar un modelo paramétrico.
• Describir los peligros de la selección del modelo basándose únicamente en datos en muestra en comparación con las ventajas de la validación del modelo fuera de muestra.

---

En esta sección se subraya la idea de que la selección de modelos es un proceso iterativo en el que los modelos se (re)formulan cíclicamente y se prueban para determinar su idoneidad antes de usarlos para la inferencia. Después de una descripción general, describimos el proceso de selección del modelo basado en:

• un conjunto de datos en muestra o de entrenamiento,
• un conjunto de datos fuera de la muestra o de prueba, y
• un método que combina estos enfoques conocido como validación cruzada.

4.2.1 Selección del Modelo Iterativa

En nuestro desarrollo examinamos los datos gráficamente, hipotetizamos la estructura de un modelo y comparamos los datos con un modelo candidato para formular un modelo mejorado. Box (1980) lo describe como un proceso iterativo el cual se muestra en la Figura 4.10.

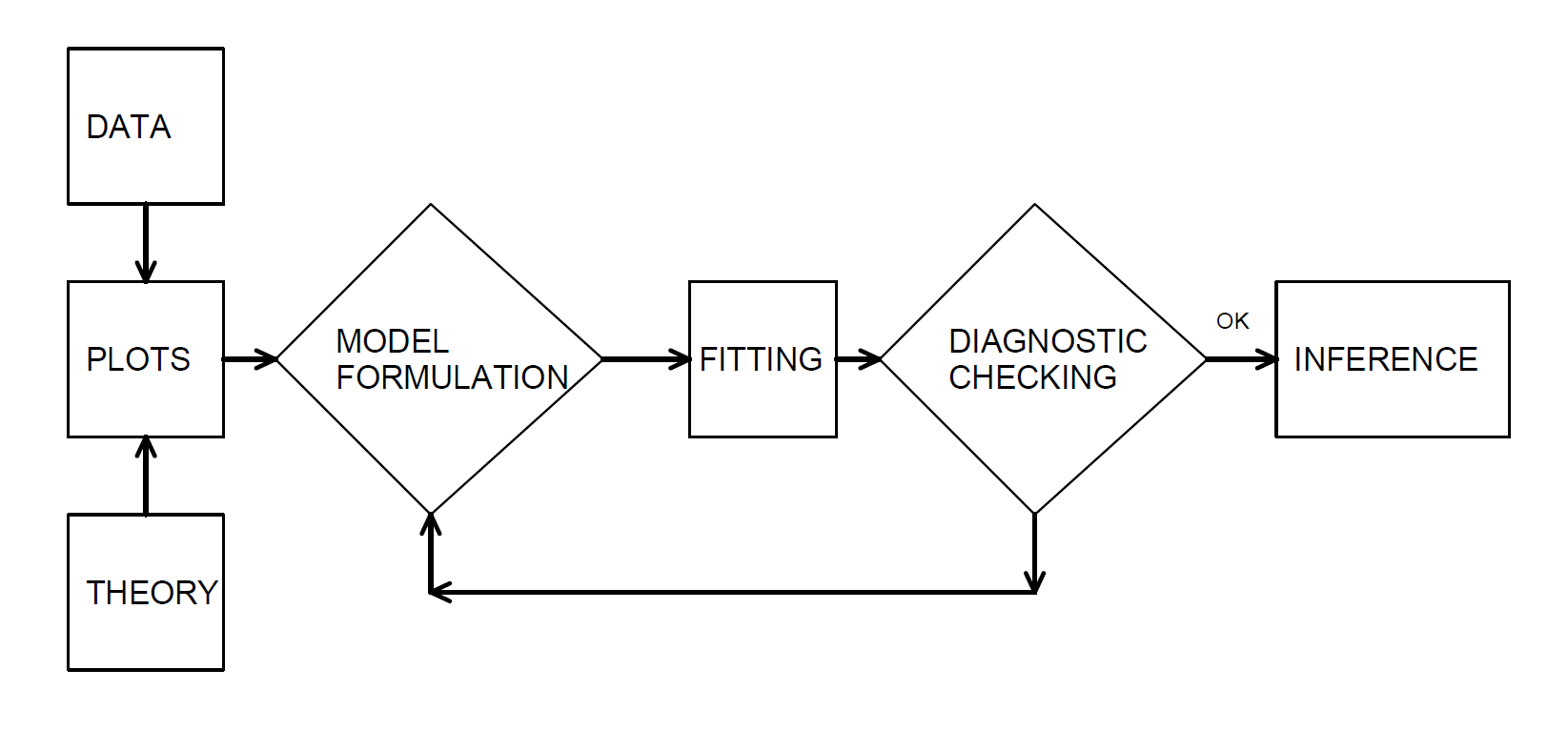
Figure 4.10: El proceso iterativo de especificación del modelo.

Este proceso iterativo proporciona un mecanismo útil para estructurar el proceso de especificación de un modelo para representar un conjunto de datos.

1. El primer paso, la etapa de formulación del modelo, se logra examinando los datos gráficamente y utilizando el conocimiento previo de las relaciones, como la teoría económica o la práctica de la industria.
2. El segundo paso en el proceso iterativo consiste en el ajuste basado en los supuestos del modelo especificado. Estas suposiciones deben ser consistentes con los datos para hacer un uso válido del modelo.
3. El tercer paso es el de comprobación de diagnóstico; los datos y el modelo deben ser coherentes entre sí antes de poder hacer inferencias adicionales. La verificación de diagnóstico es una parte importante de la formulación del modelo; puede revelar errores cometidos en pasos anteriores y proporcionar formas de corregir estos errores.

El proceso iterativo también enfatiza las habilidades que se necesitan para que la analítica funcione. Primero, se necesita estar dispuesto a resumir la información numéricamente y representarla gráficamente. En segundo lugar, es importante desarrollar una comprensión de las propiedades del modelo. Debe comprenderse cómo se comporta un modelo probabilístico para hacer coincidir un conjunto de datos con él. Tercero, las propiedades teóricas del modelo también son importantes para inferir relaciones generales basadas en el comportamiento de los datos.

4.2.2 Selección de Modelo basada en un Conjunto de Datos de Entrenamiento

Es común referirse a un conjunto de datos utilizado para el análisis como un conjunto de datos en muestra o de entrenamiento. Las técnicas disponibles para seleccionar un modelo dependen de si los resultados \(X\) son discretos, continuos o un híbrido de los dos, aunque los principios son los mismos.

Gráfico y otras medidas de resumen básicas. Comenzar resumiendo los datos gráficamente y con estadísticos que no se basen en una forma paramétrica específica, como se describe en la Sección 4.1. En concreto, es necesario representar gráficamente tanto la distribución empírica como las funciones de densidad. Particularmente, para los datos de pérdidas que contienen muchos ceros y que pueden ser asimétricos, decidir la escala apropiada (por ejemplo, logarítmica) puede representar algunas dificultades. Para datos discretos, a menudo se prefieren las tablas. Determinar los momentos muestrales, como la media y la varianza, así como los cuantiles seleccionados, incluidos el mínimo, el máximo y la mediana. Para datos discretos, la moda (o el valor más frecuente) suele ser útil.

Estos resúmenes, así como el conocimiento de la práctica profesional, permiten proponer uno o más modelos paramétricos candidatos. En general, se debe comenzar con los modelos paramétricos más simples (por ejemplo, la exponencial de un parámetro antes de una gamma de dos parámetros), introduciendo gradualmente más complejidad en el proceso de modelización.

Evaluar el modelo paramétrico candidato numérica y gráficamente. Para los gráficos, se pueden utilizar las herramientas introducidas en la Sección 4.1.2 como los gráficos \(pp\) y \(qq\). Para las evaluaciones numéricas, examinar la importancia estadística de los parámetros e intentar eliminar los parámetros que no proporcionan información adicional.

Pruebas de razón de verosimilitud. Para comparar ajustes del modelo, si un modelo es un subconjunto de otro, entonces se puede utilizar una prueba de razón de verosimilitud; el enfoque general para la prueba de razón de verosimilitud se describe en las Secciones 15.4.3 y 17.3.2.

Estadísticos de bondad del ajuste. En general, los modelos no son subconjuntos unos de otros, por lo que los estadísticos generales de bondad del ajuste son útiles para comparar modelos. Los criterios de información son un tipo de estadístico de bondad de ajuste. Los ejemplos más utilizados son el Criterio de Información de Akaike (AIC) y el Criterio de Información Bayesiano (BIC) de Schwarz; se mencionan frecuentemente porque pueden generalizarse fácilmente a entornos multivariantes. La Sección 15.4.4 proporciona una descripción de estos estadísticos.

Para seleccionar la distribución adecuada, los estadísticos que comparan un ajuste paramétrico con una alternativa no paramétrica, descritos en la Sección 4.1.2.2, son útiles para la comparación de modelos. Para datos discretos, generalmente se prefiere un estadístico de bondad de ajuste (como se describe en la Sección 2.7), ya que es más intuitivo y más simple de explicar.

4.2.3 Selección de Modelo basada en un Conjunto de Datos de Prueba

Validación del modelo es el proceso de confirmar que el modelo propuesto es apropiado, especialmente a la luz de los propósitos de la investigación. Una limitación importante del proceso de selección de modelos basado solo en datos de muestra es que puede ser susceptible a indagación de datos (data-snooping), es decir, ajustar una gran cantidad de modelos a un solo conjunto de datos. Al analizar una gran cantidad de modelos, podemos sobreajustar los datos y subestimar la variación natural en nuestra representación.

Seleccionar un modelo basado solo en datos de muestra tampoco es compatible con el objetivo de la inferencia predictiva. Particularmente, en aplicaciones actuariales nuestro objetivo es hacer declaraciones sobre la nueva experiencia en lugar de sobre el conjunto de datos disponible. Por ejemplo, utilizamos la experiencia de siniestros de un año para desarrollar un modelo que se pueda usar para fijar el precio de los contratos de seguro para el año siguiente. Como analogía, podemos pensar en el conjunto de datos de entrenamiento como experiencia de un año que se utiliza para predecir el comportamiento del conjunto de datos de prueba del próximo año.

Podemos superar estas limitaciones utilizando una técnica a veces conocida como validación fuera de muestra. La situación ideal es tener disponibles dos conjuntos de datos, uno para entrenamiento o desarrollo del modelo y otro para prueba o validación del modelo. Inicialmente desarrollamos uno o varios modelos en el primer conjunto de datos que llamamos nuestros modelos candidatos. Luego, el rendimiento relativo de los modelos candidatos se puede medir en el segundo conjunto de datos. De esta manera, los datos utilizados para validar el modelo no se ven afectados por los procedimientos utilizados para formular el modelo.

División aleatoria de los datos. Desafortunadamente, rara vez estarán disponibles dos conjuntos de datos para el investigador. Sin embargo, podemos implementar el proceso de validación dividiendo el conjunto de datos en submuestras de entrenamiento y prueba, respectivamente. La Figura 4.11 ilustra la división de los datos.

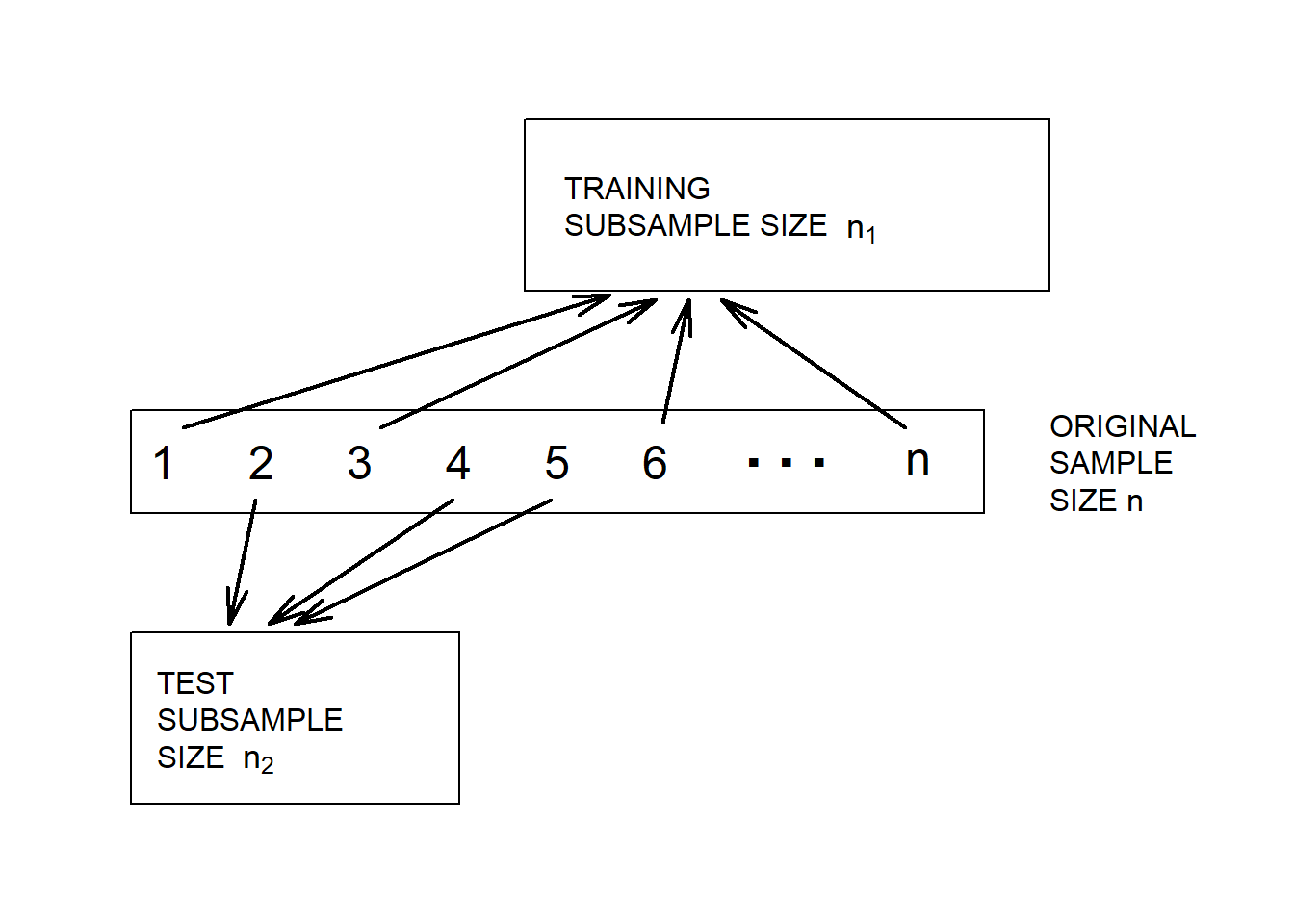
Figure 4.11: Validación del modelo. Un conjunto de datos se divide aleatoriamente en dos submuestras.

Diferentes proporciones se recomiendan para la asignación a las muestras de entrenamiento y prueba. Snee (1977) sugiere que la división de datos no se realice a menos que el tamaño de la muestra sea moderadamente grande. Las pautas de Picard and Berk (1990) muestran que cuanto mayor sea el número de parámetros a estimar, mayor será la proporción de observaciones necesarias para la submuestra de entrenamiento del modelo.

Estadísticos de validación del modelo. Gran parte de la literatura que respalda el establecimiento de un proceso de validación del modelo se basa en modelos de regresión y clasificación que puede considerarse como un problema input-output (James et al. (2013)). Es decir, tenemos varias entradas \(x_1,\ldots,x_k\) que están relacionadas con una salida \(y\) a través de una función como

\[y=\mathrm{g}\left(x_1,\ldots,x_k\right).\]

Se utiliza la muestra de entrenamiento para desarrollar una estimación de \(\mathrm{g}\), digamos, \(\hat{\mathrm{g}}\), y luego se calibra la distancia entre los resultados observados y las predicciones usando un criterio de la forma \[\begin{equation} \sum_i \mathrm{d}(y_i,\hat{\mathrm{g}}\left(x_{i1}, \ldots, x_{ik}\right) ) . \tag{4.4} \end{equation}\]

Aquí, la suma i se realiza sobre los datos de prueba. En muchas aplicaciones de regresión es común usar la distancia euclidiana al cuadrado de la forma \(\mathrm{d}(y_i,\mathrm{g})=(y_i-\mathrm{g})^2\). En aplicaciones actuariales, la distancia euclidiana \(\mathrm{d}(y_i,\mathrm{g})=|y_i-\mathrm{g}|\) a menudo se prefiere debido a la naturaleza asimétrica de los datos (valores extremos grandes de \(y\) pueden tener un gran impacto en la medida). El Capítulo 7 describe otra medida, el índice de Gini, que es útil en aplicaciones actuariales, particularmente cuando hay una gran proporción de ceros en los datos de siniestros (correspondientes a ningún siniestro).

Selección de una distribución. Nuestro enfoque hasta ahora ha sido seleccionar una distribución para un conjunto de datos que pueda usarse para la modelización actuarial sin entradas adicionales \(x_1,\ldots,x_k\). Incluso en este problema más fundamental, el enfoque de validación del modelo es adecuado. Si basamos toda la inferencia solo en datos de la muestra, entonces la tendencia es seleccionar modelos más complicados de lo necesario. Por ejemplo, se podría seleccionar una distribución con cuatro parámetros como la GB2, distribución beta generalizada de segundo tipo, cuando solo se necesita una Pareto con dos parámetros. Criterios de información como AIC criterio de información de Akaike y BIC criterio de información Bayesiano que incluyen penalizaciones a la complejidad del modelo y, por lo tanto, proporcionan cierta protección, con el uso de una muestra de prueba son la mejor garantía para lograr modelos parsimoniosos. Una cita a menudo atribuida a Albert Einstein, indica queremos “utilizar el modelo más simple (sencillo) posible pero no el más simple (simplón).”

4.2.4 Selección del Modelo basada en Validación Cruzada

Aunque la validación fuera de la muestra es el estándar más valioso en la modelización predictiva, no siempre es práctico hacerlo. La razón principal es que tenemos tamaños de muestra limitados y el criterio de selección de modelo fuera de muestra en la ecuación (4.4) depende de una división aleatoria de los datos. Lo anterior genera que diferentes analistas, incluso cuando utilizan el mismo conjunto de datos y el mismo enfoque para la modelización, puedan seleccionar diferentes modelos. Esto puede ocurrir en aplicaciones actuariales ya que se utilizan conjuntos de datos asimétricos en los que hay una elevada probabilidad de obtener algunos valores muy grandes y los valores grandes pueden tener un gran impacto en las estimaciones de los parámetros.

Procedimiento de Validación Cruzada. Alternativamente, se puede utilizar validación cruzada, de la siguiente forma.

-El procedimiento se inicia mediante el uso de un mecanismo aleatorio para dividir los datos en K subconjuntos denominados pliegues. Los analistas suelen utilizar de 5 a 10. -Después se utilizan las primeras K -1 submuestras para estimar los parámetros del modelo. Luego, se “predicen” los resultados para la submuestra K-ésima y se aplica una medida como las definidas en la ecuación (4.4) para describir el ajuste. -Ahora, se repite para cada una de las K submuestras, utilizando un estadístico acumulativo fuera de muestra para describir el ajuste.

Repetir estos pasos para varios modelos candidatos y elegir el modelo con el estadístico acumulativo fuera de muestra más bajo.

La validación cruzada se utiliza frecuentemente porque retiene la naturaliza predictiva del proceso de validación del modelo fuera de muestra pero, debido a la reutilización de los datos, es más estable que el procedimiento basado en muestras aleatorias.

4.3 Estimación utilizando Datos Modificados

---

En esta sección, se aprende a:

• Describir datos agrupados, censurados y truncados.
• Estimar distribuciones paramétricas basadas en datos agrupados, censurados y truncados
• Estimar distribuciones no paramétricas basadas en datos agrupados, censurados y truncados

---

4.3.1 Estimación Paramétrica usando Datos Modificados

La teoría básica y muchas aplicaciones se basan en observaciones individuales que son “completas” y “no modificadas,” como hemos visto en la sección anterior. La sección 3.5 introduce el concepto de observaciones que están “modificadas” debido a dos tipos comunes de limitaciones: censura y truncamiento. Por ejemplo, se suele pensar que un deducible o franquicia de seguros genera datos truncados (desde la izquierda) o los límites de la póliza genera datos censurados (desde la derecha). Este es el punto de vista del asegurador primario (el vendedor del seguro). Sin embargo, como veremos en el Capítulo 10, un reasegurador (un asegurador de una compañía de seguros) no puede observar reclamaciones menores a una cantidad, solo si existe la reclamación, un ejemplo de censura desde la izquierda. En esta sección se cubre toda la gama de alternativas. Específicamente, esta sección abordará los métodos de estimación paramétrica para tres alternativas a los datos individuales, completos y no modificados: datos censurados por intervalos disponibles solo en grupos, datos limitados o censurados, y datos que no pueden ser observados debido a truncamiento.

4.3.1.1 Estimación Paramétrica utilizando Datos Agrupados

Considerar una muestra de tamaño \(n\) observada a partir de la distribución \(F(\cdot)\), pero en grupos, de modo que solo conocemos el grupo en el que cayó cada observación, no el valor exacto. Esto se conoce como datos agrupados o censurados por intervalos. Por ejemplo, podemos estar viendo dos años consecutivos de registros anuales de empleados. Las personas empleadas en el primer año pero no en el segundo se han ido en algún momento durante el año. Con una fecha de salida exacta (datos individuales), podríamos calcular la cantidad de tiempo que estuvieron en la empresa. Sin la fecha de salida (datos agrupados), solo sabemos que partieron en algún momento durante un intervalo de un año.

Formalizando esta idea, supongamos que hay \(k\) grupos o intervalos delimitados por límites \(c_0<c_1<\cdots<c_k\). Para cada observación solo se conoce el intervalo en el que cayó (por ejemplo, \((c_{j-1},c_j)\)), no el valor exacto. Por lo tanto, solo sabemos el número de observaciones en cada intervalo. Las constantes \(\{c_0<c_1<\cdots<c_k\}\) forman alguna partición del dominio de \(F(\cdot)\). Entonces, la probabilidad de que una observación \(X_i\) caiga en el intervalo \(j\)-ésimo es \[\Pr\left (X_i \in (c_{j-1},c_j] \right)=F(c_j)-F(c_{j-1}).\]

La función de masa de probabilidad correspondiente para una observación es

\[ \begin{aligned} f(x) &= \begin{cases} F(c_1) - F(c_{0}) & \text{if }\ x \in (c_{0}, c_1]\\ \vdots & \vdots \\ F(c_k) - F(c_{k-1}) & \text{if }\ x \in (c_{k-1}, c_k]\\ \end{cases} \\ &= \prod_{j=1}^k \left\{F(c_j) - F(c_{j-1})\right\}^{I(x \in (c_{j-1}, c_j])} \end{aligned} \]

Ahora, se define \(n_j\) como el número de observaciones que caen en el intervalo \(j\)-ésimo, \((c_{j-1}, c_j]\). Por lo tanto, la función de verosimilitud (con respecto al(los) parámetro(s) \(\theta\)) es

\[ \begin{aligned} \mathcal{L}(\theta) = \prod_{j=1}^n f(x_i) = \prod_{j=1}^k \left\{F(c_j) - F(c_{j-1})\right\}^{n_j} \end{aligned} \] y el logaritmo de la función de verosimilitud es \[ \begin{aligned} L(\theta) = \ln \mathcal{L}(\theta) = \ln \prod_{j=1}^n f(x_i) = \sum_{j=1}^k n_j \ln \left\{F(c_j) - F(c_{j-1})\right\} \end{aligned} \]

Entonces, maximizar la función de verosimilitud (o, de manera equivalente, maximizar el logaritmo de la función de verosimilitud) generará los estimadores por máxima verosimilitud para los datos agrupados.

Ejemplo 4.3.1. Pregunta de Examen Actuarial.

Te dan:

1. Las pérdidas siguen una distribución exponencial con media \(\theta\).
2. Una muestra aleatoria de 20 pérdidas se distribuye de la siguiente manera: \[ {\small \begin{array}{l|c} \hline \text{Rango de Pérdidas} & \text{Frecuencia} \\ \hline [0,1000] & 7 \\ (1000,2000] & 6 \\ (2000,\infty) & 7 \\ \hline \end{array} } \]

Calcular la estimación máximo verosímil de \(\theta\).

Mostrar solución del ejemplo

Solución. \[ \begin{aligned} \mathcal{L}(\theta) &= F(1000)^7[F(2000)-F(1000)]^6[1-F(2000)]^7 \\ &= (1-e^{-1000/\theta})^7(e^{-1000/\theta} - e^{-2000/\theta})^6(e^{-2000/\theta})^7 \\ &= (1-p)^7(p-p^2)^6(p^2)^7 \\ &= p^{20}(1-p)^{13} \end{aligned} \]

donde \(p=e^{-1000/\theta}\). Maximizar esta expresión con respecto a \(p\) es equivalente a maximizar la verosimilitud con respecto a \(\theta\). El máximo ocurre en \(p=\frac{20}{33}\) y entonces \(\hat{\theta}=\frac{-1000}{\ln(20/33)}=1996,90\).

---

4.3.1.2 Datos Censurados

La censura ocurre cuando registramos solo un valor límite para una observación. La forma más común es censurar por la derecha, en la cual registramos el valor más pequeño entre el “verdadero” de la variable dependiente y una variable de censura. Usando notación, supongamos que \(X\) representa un resultado de interés, como la pérdida debido a un evento asegurado o el tiempo hasta un evento. La cuantía de censura se denota como \(C_U\). Como observaciones censuradas por la derecha, registramos \(X_U^{\ast}=\min(X,C_U)=X\wedge C_U\). También registramos si se ha producido o no la censura. Supongamos que \(\delta_U=I(X \leq C_U)\) sea una variable binaria que es 0 si se produce la censura y 1 si no es así.

Para el ejemplo que vimos en la Sección 3.4.2, \(C_U\) puede representar el límite superior de cobertura de una póliza de seguro (utilizamos \(u\) para el límite superior en esa sección). La pérdida puede exceder el valor \(C_U\), pero la aseguradora solo guarda \(C_U\) en sus registros como la cantidad pagada y no guarda el valor de la pérdida real \(X\).

De manera similar, con la censura por la izquierda, registramos el valor más grande entre la variable de interés y la variable de censura. Si se usa \(C_L\) para representar la cantidad de censura, registramos \(X_L^{\ast}=\max(X,C_L)\) junto con el indicador de censura \(\delta_L=I(X\geq C_L)\).

Como ejemplo, tenemos una breve introducción al reaseguro, seguro para aseguradores, en la Sección 3.4.4 y se verá más en el Capítulo 10. Supongamos que una reaseguradora cubrirá las pérdidas de la aseguradora mayores a \(C_L\); esto significa que el reasegurador es responsable del exceso de \(X_L^{\ast}\) sobre \(C_L\). Usando notación, esto es \(Y=X_L^{\ast}-C_L\). Para ver esto, primero considere el caso donde la pérdida del titular de la póliza \(X<C_L\). Luego, el asegurador pagará el siniestro completo y \(Y=C_L-C_L=0\), sin pérdida para el reasegurador. Para el segundo caso, si la pérdida \(X\ge C_L\), entonces \(Y=X-C_L\) representa las reclamaciones retenidas por el reasegurador. Dicho de otra manera, si ocurre una pérdida, el reasegurador registra la cuantía real si excede del límite \(C_L\) o, de lo contrario, solo registra que tuvo una pérdida de \(0\).

4.3.1.3 Datos Truncados

Las observaciones censuradas se registran para su estudio, aunque de forma limitada. En contraste, los resultados truncados son un tipo de datos ausentes. Un resultado se trunca potencialmente cuando la disponibilidad de una observación depende del resultado.

En el seguro, es común que las observaciones sean truncadas por la izquierda en \(C_L\) cuando la cantidad es \[ \begin{aligned} Y &= \left\{ \begin{array}{cl} \text{nosotros no observamos }X & X < C_L \\ X & X \geq C_L \end{array} \right.\end{aligned} . \]

En otras palabras, si \(X\) es menor que el umbral \(C_L\), entonces no se observa.

Para un ejemplo que vimos en la Sección 3.4.1, \(C_L\) puede representar el deducible de una póliza de seguro (utilizamos \(d\) para el deducible en esa sección). Si la pérdida asegurada es menor que el deducible, entonces el asegurador no puede observar ni registrar la pérdida. Si la pérdida excede el deducible, el exceso de \(X-C_L\) es el siniestro que cubre la aseguradora. En la Sección 3.4.1, definimos la pérdida por pago como \[ Y^{P} = \left\{ \begin{matrix} \text{Indefinido} & X \le d \\ X - d & X > d \end{matrix} \right. , \] de modo que si una pérdida excede un deducible, registramos la cuantía en exceso \(X-d\). Esto es muy importante cuando se consideran las cuantías que pagará la aseguradora. Sin embargo, para propósitos de estimación de esta sección, importa poco si restamos una constante conocida como \(C_L=d\). Entonces, para nuestra variable truncada \(Y\), usamos la convención más simple y no restamos \(d\).

De manera similar para datos truncados por la derecha, si \(X\) excede un umbral \(C_U\), entonces no se observa. En este caso, la cantidad es \[ \begin{aligned} Y &= \left\{ \begin{array}{cl} X & X \leq C_U \\ \text{nosotros no observamos }X & X > C_U. \end{array} \right.\end{aligned} \]

Los ejemplos clásicos de truncamiento por la derecha incluyen \(X\) como medida de distancia a una estrella. Cuando la distancia excede un cierto nivel \(C_U\), la estrella ya no es observable.

La Figura 4.12 compara observaciones truncadas y censuradas. Los valores de \(X\) que son mayores que el límite “superior” \(C_U\) no se observan (truncados a la derecha), mientras que los valores de \(X\) que son menores que el límite “inferior” \(C_L\) se observan, pero se observan como \(C_L\) en lugar del valor real de \(X\) (censura a la izquierda).

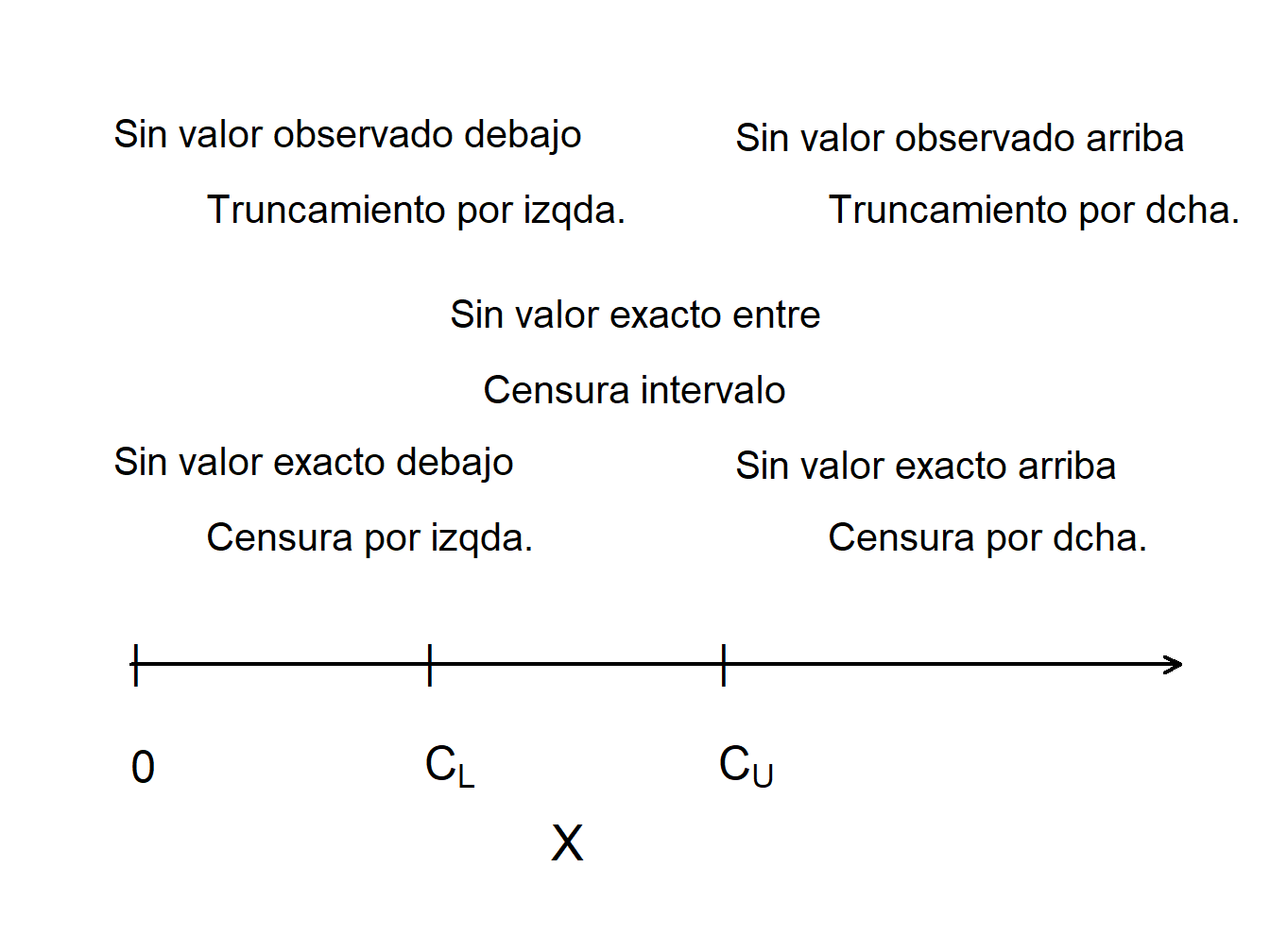
Figure 4.12: Censura y Truncamiento

---

Mostrar ejemplo de estudio de mortalidad

Ejemplo: estudio de mortalidad. Supongamos que se está realizando un estudio de dos años de mortalidad de sujetos de alto riesgo, comenzando el 1 de enero de 2010 y terminando el 1 de enero de 2012. Figura 4.13 representa gráficamente los seis tipos de sujetos reclutados. Para cada sujeto, el comienzo de la flecha representa que el sujeto fue reclutado y el final de la flecha representa el tiempo del evento. Por lo tanto, la flecha representa el tiempo de exposición.

Figure 4.13: Cronología de varios sujetos en prueba en un estudio de mortalidad

• Tipo A: Censurado por la derecha. Este sujeto está vivo al principio y al final del estudio. Debido a que no se conoce el momento de la muerte al final del estudio, está censurado correctamente. La mayoría de los sujetos son de tipo A.
• Tipo B- Información completa está disponible para un sujeto tipo B. El sujeto está vivo al comienzo del estudio y la muerte ocurre dentro del período de observación.
• Tipo C: Censurado por la derecha y truncado a la izquierda. Un sujeto de tipo C está censurado por la derecha, ya que la muerte ocurre después del período de observación. Sin embargo, el sujeto ingresó después del inicio del estudio y se dice que tiene un tiempo de entrada retrasado. Debido a que el sujeto no habría sido observado si la muerte hubiera ocurrido antes de la entrada, se trunca a la izquierda.
• Tipo D: truncado por la izquierda. Un sujeto de tipo D también ha retrasado la entrada. Debido a que la muerte ocurre dentro del período de observación, este individuo no está censurado a la derecha.
• Tipo E: truncado por la izquierda. Un sujeto tipo E no está incluido en el estudio porque la muerte ocurre antes del período de observación.
• Tipo F: truncado por la derecha. Del mismo modo, un sujeto tipo F no está incluido porque el tiempo de entrada ocurre después del período de observación.

---

Para resumir, para el resultado \(X\) y las constantes \(C_L\) y \(C_U\),

Tipo de Limitación	Variable Limitada	Registro de Información
Censura por drcha.	\(X_U^{\ast}= \min(X,C_U)\)	\(\delta_U= I(X \leq C_U)\)
Censura por izda.	\(X_L^{\ast}= \max(X,C_L)\)	\(\delta_L= I(X \geq C_L)\)
Censura por intervalo
Truncamiento drcha.	\(X\)	observa \(X\) si \(X \leq C_U\)
Truncamiento izda.	\(X\)	observa \(X\) si \(X \geq C_L\)

4.3.1.4 Estimación paramétrica utilizando datos censurados y truncados

Para simplificar, asumimos valores de censura no aleatorios y una variable continua \(X\). Empezamos considerando el caso de datos censurados a la derecha donde registramos \(X_U^{\ast}=\min(X,C_U)\) y el indicador de censura \(\delta=I(X \leq C_U)\). Si la censura ocurre, de modo que \(\delta = 0\), entonces \(X\geq C_U\) y la probabilidad es \(\Pr(X \geq C_U)=1-F(C_U)\). Si la censura no ocurre, de modo que \(\delta=1\), entonces \(X<C_U\) y la verosimilitud es \(f(x)\). Resumiendo, tenemos la verosimilitud de una sola observación como

\[ \begin{aligned} \left\{ \begin{array}{ll} 1-F(C_U) & \text{if }\delta=0 \\ f(x) & \text{if } \delta = 1 \end{array} \right. = \left\{ f(x)\right\}^{\delta} \left\{1-F(C_U)\right\}^{1-\delta} . \end{aligned} \]

La expresión de a la derecha nos permite presentar la verosimilitud de manera más compacta. Ahora, para una muestra iid de tamaño \(n\), la verosimilitud es

\[ \mathcal{L} = \prod_{i=1}^n \left\{ f(x_i)\right\}^{\delta_i} \left\{1-F(C_{Ui})\right\}^{1-\delta_i} = \prod_{\delta_i=1} f(x_i) \prod_{\delta_i=0} \{1-F(C_{Ui})\}, \]

con tiempos de censura potenciales \(\{C_{U1},\ldots, C_{Un} \}\). Aquí, la notación “\(\prod_{\delta_i=1}\)” significa el producto de las observaciones sin censura, y de manera similar para “\(\prod_{\delta_i=0}\).”

Por otro lado, los datos truncados se tratan en inferencia de verosimilitud mediante probabilidades condicionadas. En concreto, ajustamos la contribución a la verosimilitud dividiendo por la probabilidad de que se haya observado la variable. En resumen, tenemos las siguientes contribuciones a la función de verosimilitud para seis tipos de resultados: \[ {\small \begin{array}{lc} \hline \text{Resultado} & \text{Contribución en la Verosimilitud} \\ \hline \text{Valor exacto} & f(x) \\ \text{Censura por la derecha} & 1-F(C_U) \\ \text{Censura por la izquierda} & F(C_L) \\ \text{Truncamiento por la derecha} & f(x)/F(C_U) \\ \text{Truncamiento por la izquierda} & f(x)/(1-F(C_L)) \\ \text{Censura por intervalo } & F(C_U)-F(C_L) \\ \hline \end{array} } \]

Para resultados conocidos y datos censurados, la verosimilitud es \[\mathcal{L}(\theta) = \prod_{E} f(x_i) \prod_{R} \{1-F(C_{Ui})\} \prod_{L} F(C_{Li}) \prod_{I} (F(C_{Ui})-F(C_{Li})),\] donde “\(\prod_{E}\)” es el producto sobre las observaciones con valores Exactos (E), y de manera similar para los datos censurados por la Derecha (R), Izquierda (L) y en Intervalo (I).

Para datos censurados por la derecha y truncados por la izquierda, la probabilidad es \[\mathcal{L} = \prod_{E} \frac{f(x_i)}{1-F(C_{Li})} \prod_{R} \frac{1-F(C_{Ui})}{1-F(C_{Li})},\] y de manera similar para otras combinaciones. Para obtener más información, considere lo siguiente.

---

Mostrar caso particular – Distribución Exponencial

Caso especial: Distribución exponencial. Considere los datos que están censurados por la derecha y truncados por la izquierda, con variables aleatorias \(X_i\) que se distribuyen exponencialmente con media \(\theta\). Con estas especificaciones, recuerde que \(f(x) = \theta^{-1} \exp(-x/\theta)\) y \(F(x) = 1-\exp(-x/\theta)\).

Para este caso particular, la log verosimilitud es

\[ \begin{aligned} L(\theta) &= \sum_{E} \left\{ \ln f(x_i) - \ln (1-F(C_{Li})) \right\} + \sum_{R}\left\{ \ln (1-F(C_{Ui}))- \ln (1-\mathrm{F}(C_{Li})) \right\}\\ &= \sum_{E} (-\ln \theta -(x_i-C_{Li})/\theta ) -\sum_{R} (C_{Ui}-C_{Li})/\theta . \end{aligned} \]

Para simplificar la notación, definimos \(\delta_i=I(X_i\geq C_{Ui})\) como una variable binaria que indica la censura a la derecha. Sea \(X_i^{\ast\ast} = \min(X_i,C_{Ui})-C_{Li}\) la cantidad que la variable observada excede el límite inferior de truncamiento. Con esto, la log verosimilitud es

\[\begin{equation} L(\theta) = - \sum_{i=1}^n ((1-\delta_i) \ln \theta + \frac{x_i^{\ast \ast}}{\theta}). \tag{4.5} \end{equation}\]

Derivando con respecto al parámetro \(\theta\) e igualando a cero se obtiene el estimador de máxima verosimilitud \[\widehat{\theta} = \frac{1}{n_u} \sum_{i=1}^n x_i^{\ast \ast},\]

donde \(n_u = \sum_i (1-\delta_i)\) es el número de datos no censurados.

---

Ejemplo 4.3.2. Pregunta de Examen Actuarial. Te dan:

1. Una muestra de pérdidas es: 600 700 900
2. No hay información disponible sobre pérdidas de 500 o menos.
3. Se supone que las pérdidas siguen una distribución exponencial con media \(\theta\).

Calcular el estimador de máxima verosimilitud de \(\theta\).

Mostrar solución del ejemplo

Solución. Estas observaciones se truncan en 500. La contribución de cada observación a la función de verosimilitud es \[\frac{f(x)}{1-F(500)} = \frac{\theta^{-1}e^{-x/\theta}}{e^{-500/\theta}}\]

Entonces la función de verosimilitud es

\[\mathcal{L}(\theta)= \frac{\theta^{-1} e^{-600/\theta} \theta^{-1} e^{-700/\theta} \theta^{-1} e^{-900/\theta}}{(e^{-500/\theta})^3} = \theta^{-3}e^{-700/\theta}\]

El logaritmo de la verosimilitud es

\[L(\theta) = \ln\mathcal{L}(\theta) = -3\ln \theta - 700\theta^{-1}\]

Maximizando esta expresión, estableciendo la derivada con respecto a \(\theta\) igual a 0, tenemos

\[L'(\theta) = -3\theta^{-1} + 700\theta^{-2} = 0 \ \Rightarrow \ \hat{\theta} = \frac{700}{3} = 233,33\]

---

Ejemplo 4.3.3. Pregunta de Examen Actuarial. Se le proporciona la siguiente información sobre una muestra aleatoria:

1. El tamaño de la muestra es igual a cinco.
2. La muestra es de una distribución de Weibull con \(\tau = 2\).
3. Se sabe que dos de las observaciones de la muestra exceden 50, y las tres observaciones restantes son 20, 30 y 45.

Calcule el estimador de máxima verosimilitud de \(\theta\).

Mostrar solución del ejemplo

Solución. La función de verosimilitud es

\[ \begin{aligned} \mathcal{L}(\theta) &= f(20) f(30) f(45) [1-F(50)]^2 \\ &= \frac{2(20/\theta)^2 e^{-(20/\theta)^2}}{20} \frac{2(30/\theta)^2 e^{-(30/\theta)^2}}{30} \frac{2(45/\theta)^2 e^{-(45/\theta)^2}}{45}(e^{-(50/\theta)^2})^2 \\ &\propto \frac{1}{\theta^6} e^{-8325/\theta^2} \end{aligned} \]

El logaritmo natural de la expresión anterior es \(-6\ln\theta-\frac{8325}{\theta^2}\). Maximizando esta expresión al fijar su derivada igual a 0, obtenemos

\[\frac{-6}{\theta} + \frac{16650}{\theta^3} = 0 \ \Rightarrow \ \hat{\theta} = \left(\frac{16650}{6}\right)^{\frac{1}{2}} = 52,6783\]

---

4.3.2 Estimación no Paramétrica Utilizando Datos Modificados

Los estimadores no paramétricos proporcionan puntos de referencia útiles, por lo que es útil comprender los procedimientos de estimación para datos agrupados, censurados y truncados.

4.3.2.1 Datos Agrupados

Como hemos visto en la Sección 4.3.1.1, las observaciones pueden agruparse (también denominadas censuradas por intervalos) en el sentido de que solo las observamos como pertenecientes a uno de los \(k\) intervalos de la forma \((c_{j-1},c_j]\), para \(j=1,\ldots,k\). En los límites, la función de distribución empírica se define de la manera habitual:

\[ F_n(c_j) = \frac{\text{número de observaciones } \le c_j}{n}. \]

Para otros valores de \(x \in (c_{j-1},c_j)\), podemos estimar la función de distribución con el estimador ogive, que interpola linealmente entre \(F_n(c_{j-1})\) y \(F_n(c_j)\), es decir, los valores de los límites \(F_n(c_{j-1})\) y \(F_n (c_j)\) están conectados con una línea recta. Esto puede expresarse formalmente como \[F_n(x) = \frac{c_j-x}{c_j-c_{j-1}} F_n(c_{j-1}) + \frac{x-c_{j-1}}{c_j-c_{j-1}} F_n(c_j) \ \ \ \text{para } c_{j-1} \le x < c_j\]

La densidad correspondiente es \[f_n(x) = F^{\prime}_n(x) = \frac{F_n(c_j)-F_n(c_{j-1})}{c_j - c_{j-1}} \ \ \ \text{para } c_{j-1} \le x < c_j .\]

---

Ejemplo 4.3.4. Pregunta de Examen Actuarial.

Se le proporciona la siguiente información sobre los cantidades reclamadas para 100 siniestros:

\[ {\small \begin{array}{r|c} \hline \text{Tamaño del Siniestro} & \text{Número de Siniestros } \\ \hline 0 – 1.000 & 16 \\ 1.000 – 3.000 & 22 \\ 3.000 – 5.000 & 25 \\ 5.000 – 10.000 & 18 \\ 10.000 – 25.000 & 10 \\ 25.000 – 50.000 & 5 \\ 50.000 – 100.000 & 3 \\ \text{mayor } 100.000 & 1 \\ \hline \end{array} } \]

Usando el estimador ogive, calcule la estimación de la probabilidad de que un siniestro elegido al azar esté entre 2000 y 6000.

Mostrar solución del ejemplo

Solución. En los límites, la función de distribución empírica se define de la manera habitual, por lo que tenemos \[F_{100}(1000) = 0,16, \ F_{100}(3000)=0,38, \ F_{100}(5000)=0,63, \ F_{100}(10000)=0,81.\] Para otros tamaños del siniestro, el estimador ogive interpola linealmente entre estos valores: \[F_{100}(2000) = 0,5F_{100}(1000) + 0,5F_{100}(3000) = 0,5(0,16)+0,5(0,38)=0,27\] \[F_{100}(6000)=0,8F_{100}(5000)+0,2F_{100}(10000) = 0,8(0,63)+0,2(0,81)=0,666\] Por lo tanto, la probabilidad de que una reclamación esté entre 2000 y 6000 es \(F_{100}(6000) - F_{100}(2000) = 0,666-0,27 = 0,396\).

---

4.3.2.2 Función de Distribución Empírica Censurada por la Derecha

Puede ser útil calibrar los estimadores paramétricos con métodos no paramétricos que no se basen en una forma paramétrica de la distribución. El estimador de límite de producto propuesto por (Kaplan and Meier 1958) es un estimador de la función de distribución bien conocido en presencia de censura.

Motivación para el Estimador de Límite de Producto de Kaplan-Meier. Para explicar por qué el límite de producto funciona tan bien con observaciones censuradas, volvamos primero al caso “habitual” sin censura. Aquí, la función de distribución empírica \(F_n(x)\) es un estimador insesgado de la función de distribución \(F(x)\). Esto se debe a que \(F_n(x)\) es el promedio de las variables indicadoras, cada una de las cuales es insesgada, es decir, \(\mathrm{E~}I(X_i \le x) = \Pr(X_i \le x) = F(x)\).

Ahora supongamos que la variable aleatoria está censurada por la derecha por una cantidad límite, por ejemplo, \(C_U\), de modo que registramos el menor de los dos, \(X^* = \min(X, C_U)\). Para valores de \(x\) que son menores que \(C_U\), la variable indicadora todavía proporciona un estimador insesgado de la función de distribución antes de alcanzar el límite de censura. Es decir, \(\mathrm{E ~}I(X^* \le x) = F(x)\) porque \(I(X^* \le x) = I(X \le x)\) para \(x<C_U\). Del mismo modo, \(\mathrm{E~}I(X^*> x) = 1-F(x) = S(x)\). En cambio, para \(x>C_U\), \(I(X^* \le x)\) en general no es un estimador insesgado de \(F(x)\).

Como alternativa, consideremos dos variables aleatorias que tienen diferentes límites de censura. Por ejemplo, supongamos que observamos \(X_1^* = \min(X_1, 5)\) y \(X_2^* = \min(X_2, 10)\), donde \(X_1\) y \(X_2\) son extracciones independientes de la misma distribución. Para \(x\le 5\), la función de distribución empírica \(F_2(x)\) es un estimador insesgado de \(F(x)\). Sin embargo, para \(5<x \le 10\), la primera observación no puede usarse para la función de distribución debido a la limitación de censura. En cambio, la estrategia desarrollada por (Kaplan and Meier 1958) es usar \(S_2(5)\) como estimador de \(S(5)\) y luego usar la segunda observación para estimar la función de supervivencia condicional a la supervivencia al tiempo 5, \(\Pr(X>x|X>5) = \frac {S(x)}{S(5)}\). Específicamente, para \(5<x \le 10\), el estimador de la función de supervivencia es

\[ \hat{S}(x) = S_2(5) \times I(X_2^* > x ) . \]

Estimador del límite de producto de Kaplan-Meier. Ampliando esta idea, para cada observación \(i\), sea \(u_i\) el límite superior de censura (\(= \infty\) si no hay censura). Por lo tanto, el valor registrado es \(x_i\) en el caso de no censura y \(u_i\) si hay censura. Supongamos que \(t_{1}<\cdots<t_{k}\) sean \(k\) puntos distintos en los que se produce una pérdida sin censura, y que \(s_j\) sea el número de pérdidas sin censura \(x_i\)’s en \(t_{j}\). El conjunto de riesgo correspondiente es el número de observaciones que están activas (no censuradas) en un valor menor que \(t_{j}\), denotado como \(R_j=\sum_{i = 1}^n I(x_i \geq t_{j})+\sum_{i = 1}^n I(u_i \geq t_{j})\).

Con esta notación, el estimador del límite de producto de la función de distribución es \[\begin{equation} \hat{F}(x) = \left\{ \begin{array}{ll} 0 & x<t_{1} \\ 1-\prod_{j:t_{j} \leq x}\left( 1-\frac{s_j}{R_{j}}\right) & x \geq t_{1} \end{array} \right. .\tag{4.6} \end{equation}\]

Como de costumbre, la estimación correspondiente de la función de supervivencia es \(\hat{S}(x) = 1 - \hat{F}(x)\).

---

Ejemplo 4.3.5. Pregunta de Examen Actuarial. La siguiente es una muestra de 10 pagos:

\[ \begin{array}{cccccccccc} 4 &4 &5+ &5+ &5+ &8 &10+ &10+ &12 &15 \\ \end{array} \]

donde \(+\) indica que una pérdida ha excedido el límite de la póliza.

Usando el estimador de límite de producto de Kaplan-Meier, calcule la probabilidad de que la pérdida en una póliza exceda 11, \(\hat{S}(11)\).

Mostrar solución del ejemplo

Solución. Hay cuatro tiempos de eventos (observaciones no censuradas). Para cada tiempo \(t_j\), podemos calcular el número de eventos \(s_j\) y el conjunto de riesgo \(R_j\) de la siguiente manera:

\[ \begin{array}{cccc} \hline j & t_j & s_j & R_j \\ \hline 1 & 4 & 2 & 10 \\ 2 & 8 & 1 & 5 \\ 3 & 12 & 1 & 2 \\ 4 & 15 & 1 & 1 \\ \hline \end{array} \]

Asi, la estimación de Kaplan-Meier de \(S(11)\) es \[ \begin{aligned} \hat{S}(11) &= \prod_{j:t_j\leq 11} \left( 1- \frac{s_j}{R_j} \right) = \prod_{j=1}^{2} \left( 1- \frac{s_j}{R_j} \right)\\ &= \left(1-\frac{2}{10} \right) \left(1-\frac{1}{5} \right) = (0,8)(0,8)= 0,64. \\ \end{aligned} \]

---

Ejemplo. 4.3.6. Siniestros con Daños Corporales. Consideramos nuevamente los datos de la aplicación de Derrig, Ostaszewski, and Rempala (2001) de siniestros por daños corporales en automóviles en Boston, que se presentaron en el Ejemplo 4.1.11. En ese ejemplo, omitimos los siniestros 17 que fueron censurados por los límites de la póliza. Ahora, incluimos el conjunto de datos completo y utilizamos el estimador del límite de producto de Kaplan-Meier para estimar la función de supervivencia. Esto se muestra en la Figura 4.14.

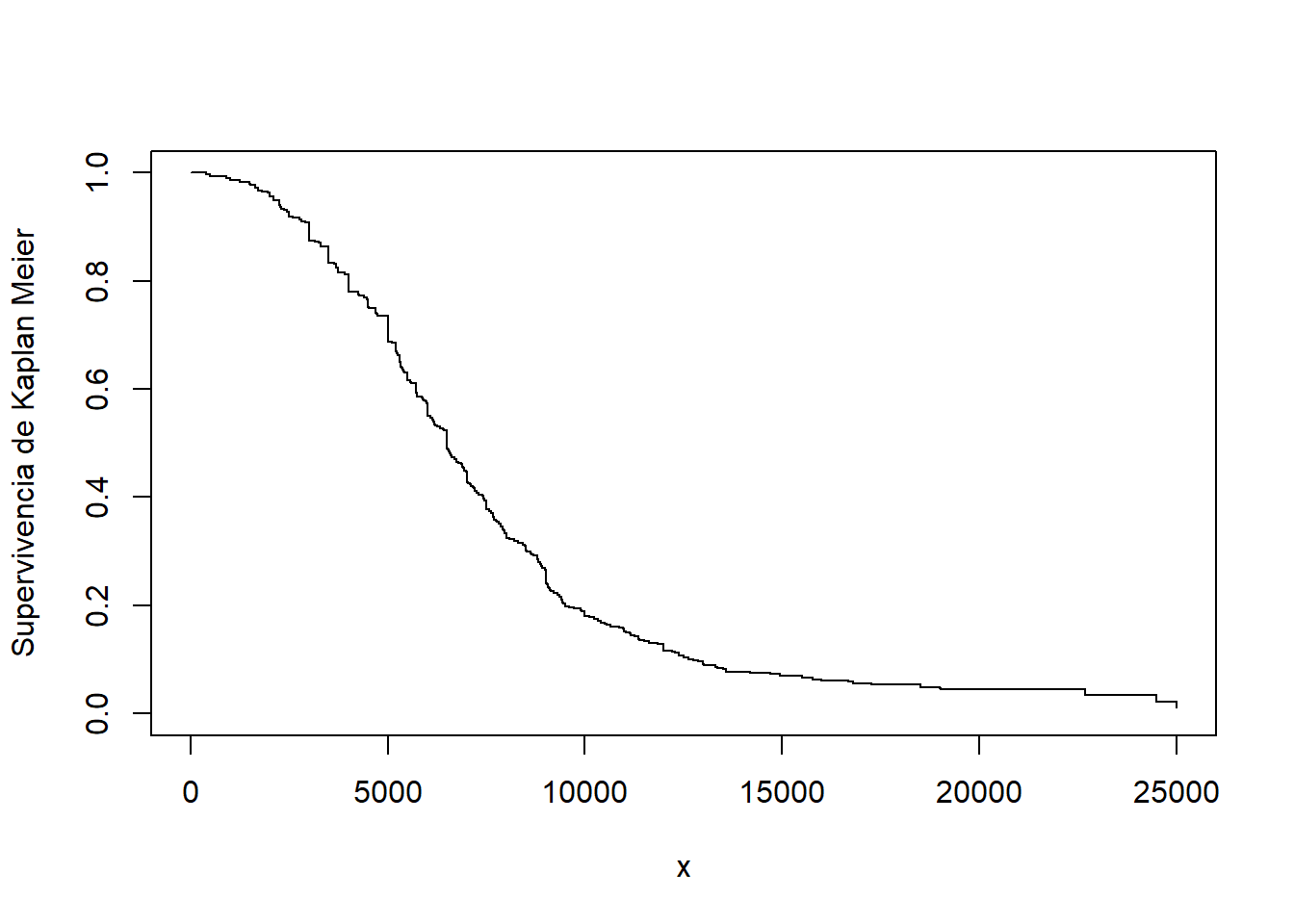
Figure 4.14: Estimación de Kaplan-Meier de la función de supervivencia para siniestros por daños corporales

Mostrar código R

library(survival)                # para Surv(), survfit()
## KM estimación
KM0 <- survfit(Surv(AmountPaid, UnCensored) ~ 1,  type="kaplan-meier", data=BIData)
plot(KM0, conf.int=FALSE, xlab="x",ylab="Supervivencia de Kaplan Meier ")

---

4.3.2.3 Función de Distribución Empírica Censurada por la Derecha, Truncada por la Izquierda

Además de la censura por la derecha, ahora ampliamos el marco para permitir datos truncados por la izquierda. Como antes, para cada observación \(i\), sea \(u_i\) el límite superior de censura (\(= \infty\) si no hay censura). Además, sea \(d_i\) el límite inferior de truncamiento (0 si no hay truncamiento). Por lo tanto, el valor registrado (si es mayor que \(d_i\)) es \(x_i\) en el caso de no censura y \(u_i\) si hay censura. Supongamos que \(t_{1} <\cdots <t_{k}\) son \(k\) puntos distintos en los que se produce un evento de interés, y que \(s_j\) son el número de eventos registrados \(x_i\)’s en el punto de tiempo \(t_{j}\). El conjunto de riesgos correspondiente es \[R_j = \sum_{i=1}^n I(x_i \geq t_{j}) + \sum_{i=1}^n I(u_i \geq t_{j}) - \sum_{i=1}^n I(d_i \geq t_{j}).\]

Con esta nueva definición del conjunto de riesgos, el estimador del límite de producto de la función de distribución es como en la ecuación (4.6).

Fórmula de Greenwood. (Greenwood 1926) obtuvo la fórmula para que la varianza estimada del estimador de límite de producto sea \[\widehat{Var}(\hat{F}(x)) = (1-\hat{F}(x))^{2} \sum _{j:t_{j} \leq x} \dfrac{s_j}{R_{j}(R_{j}-s_j)}.\]

El método de R survfit utiliza un objeto de datos de supervivencia y crea un nuevo objeto que contiene la estimación de Kaplan-Meier de la función de supervivencia junto con los intervalos de confianza. El método de Kaplan-Meier (type = 'kaplan-meier') se usa por defecto para construir una estimación de la curva de supervivencia. La función de supervivencia discreta resultante tiene puntos de masa en los tiempos de evento observados (fechas de alta) \(t_j\), donde la probabilidad de supervivencia de un evento a esa duración se estima como el número de eventos observados en la duración \(s_j\) dividido por el número de sujetos expuestos o ‘en riesgo’ justo antes de la duración del evento \(R_j\).

Dos tipos alternativos de estimación también están disponibles para el método survfit. La alternativa (type='fh2') maneja los empates, en esencia, al suponer que ocurren varios eventos con la misma duración en un orden arbitrario. Otra alternativa (type='fleming-harrington') usa el estimador de Nelson-Aalen (see (Aalen 1978)) en la estimación de la función de riesgo (hazard) acumulado para obtener una estimación de la función de supervivencia. El riesgo acumulado estimado \(\hat{H}(x)\) comienza en cero y se incrementa en cada evento observado de duración \(t_j\) por el número de eventos \(s_j\) dividido por el número en riesgo \(R_j\). Con la misma notación anterior, el estimador de Nelson-Aalen de la función de distribución es

\[ \begin{aligned} \hat{F}_{NA}(x) &= \left\{ \begin{array}{ll} 0 & x<t_{1} \\ 1- \exp \left(-\sum_{j:t_{j} \leq x}\frac{s_j}{R_j} \right) & x \geq t_{1} \end{array} \right. .\end{aligned} \]

Cabe tener en cuenta que la expresión anterior es el resultado del estimador de Nelson-Aalen de la función de riesgo acumulado \[\hat{H}(x) = \sum_{j: t_j \leq x}\frac{s_j}{R_j}\] y la relación entre la función de supervivencia y la función de riesgo acumulado es \(\hat{S}_{NA}(x) = e^{-\hat{H}(x)}\).

---

Ejemplo 4.3.7. Pregunta de Examen Actuarial.

Para la observación \(i\) de un estudio de supervivencia:

• \(d_i\) es el punto de truncamiento a la izquierda
• \(x_i\) es el valor observado si no está censurado a la derecha
• \(u_i\) es el valor observado si se censura a la derecha

Te dan:

\[ {\small \begin{array}{c|cccccccccc} \hline \text{Observación } (i) & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ \hline d_i & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1,3 & 1,5 & 1,6\\ x_i & 0,9 & - & 1,5 & - & - & 1,7 & - & 2,1 & 2,1 & - \\ u_i & - & 1,2 & - & 1,5 & 1,6 & - & 1,7 & - & - & 2,3 \\ \hline \end{array} } \]

Calcular la estimación del límite de producto de Kaplan-Meier, \(\hat{S}(1,6)\)

Mostrar solución del ejemplo

Solución. Recordemos el conjunto de riesgo \(R_j = \sum_{i=1}^n \left\{ I(x_i \geq t_{j}) + I(u_i \geq t_{j}) - I(d_i \geq t_{j}) \right\}\). Entonces

\[ \begin{array}{ccccc} \hline j & t_j & s_j & R_j & \hat{S}(t_j) \\ \hline 1 & 0,9 & 1 & 10-3 = 7 & 1-\frac{1}{7} = \frac{6}{7} \\ 2 & 1,5 & 1 & 8-2 = 6 & \frac{6}{7}\left( 1 - \frac{1}{6} \right) = \frac{5}{7}\\ 3 & 1,7 & 1 & 5-0 = 5 & \frac{5}{7}\left( 1 - \frac{1}{5} \right) = \frac{4}{7}\\ 4 & 2,1 & 2 & 3 & \frac{4}{7}\left( 1 - \frac{2}{3}\right) = \frac{4}{21}\\ \hline \end{array} \]

La estimación de Kaplan-Meier es por lo tanto \(\hat{S}(1,6) = \frac{5}{7}\).

---

Ejemplo 4.3.8. Pregunta de Examen Actuarial. – Continuación.

1. Usando el estimador de Nelson-Aalen, calcular la probabilidad de que la pérdida en una póliza exceda 11, \(\hat{S}_{NA}(11)\).
2. Calcular la aproximación de Greenwood de la varianza de la estimación del límite del producto \(\hat{S}(11)\).

Mostrar solución del ejemplo

Solución. Como antes, hay cuatro tiempos con eventos (observaciones no censuradas). Para cada tiempo \(t_j\) podemos calcular el número de eventos \(s_j\) y el conjunto de riesgo \(R_j\) de la siguiente manera: \[ \begin{array}{cccc} \hline j & t_j & s_j & R_j \\ \hline 1 & 4 & 2 & 10 \\ 2 & 8 & 1 & 5 \\ 3 & 12 & 1 & 2 \\ 4 & 15 & 1 & 1 \\ \hline \end{array} \]

El estimador de Nelson-Aalen de \(S(11)\) es \(\hat{S}_{NA}(11)=e^{-\hat{H}(11)} = e^{-0,4} = 0,67\), de modo que \[ \begin{aligned} \hat{H}(11) &= \sum_{j:t_j\leq 11} \frac{s_j}{R_j} = \sum_{j=1}^{2} \frac{s_j}{R_j} \\ &= \frac{2}{10} + \frac{1}{5} = 0,2 + 0,2 = 0,4 .\\ \end{aligned} \] Del ejercicio anterior, la estimación de Kaplan-Meier de \(S(11)\) es \(\hat{S}(11) = 0,64\). Entonces, la estimación de Greenwood de la varianza de la estimación del límite del producto de \(S(11)\) es \[ \begin{aligned} \widehat{Var}(\hat{S}(11)) &= (\hat{S}(11))^2 \sum_{j:t_j\leq 11} \frac{s_j}{R_j(R_j-s_j)} &= (0,64)^2 \left(\frac{2}{10(8)} + \frac{1}{5(4)} \right) = 0,0307. \\ \end{aligned} \]

---

4.4 Inferencia Bayesiana

---

En esta sección aprende a:

• Describir el modelo bayesiano como una alternativa al enfoque frecuentista y resumir los cinco componentes de este enfoque de modelización.
• Describir las distribuciones a posteriori de los parámetros y utilizar estas distribuciones para predecir nuevos resultados.
• Utilizar distribuciones conjugadas para determinar las distribuciones a posteriori de los parámetros.

---

4.4.1 Introducción a la Inferencia Bayesiana

Hasta este punto, nuestros métodos inferenciales se han centrado en el entorno frecuentista, en el que se extraen muestras repetidamente de una población. El vector de parámetros \(\boldsymbol \theta\) es fijo pero desconocido, mientras que los resultados \(X\) son realizaciones procedentes de variables aleatorias.

En contraste, bajo el marco Bayesiano, consideramos los parámetros del modelo y los datos como variables aleatorias. No estamos seguros de los valores de los parámetros \(\boldsymbol \theta\) y utilizamos herramientas de probabilidad para reflejar esta incertidumbre.

Para tener una idea del marco bayesiano, recordemos primero la regla de Bayes \[ \Pr(parámetros|datos) = \frac{\Pr(datos|parámetros) \times \Pr(parámetros)}{\Pr(datos)} \]

donde

• \(\Pr(parámetros)\) es la distribución de los parámetros, conocida como la distribución a priori.
• \(\Pr(datos|parámetros)\) es la distribución de muestreo. En un contexto frecuentista, se usa para realizar inferencias sobre los parámetros y se conoce como probabilidad.
• \(\Pr(parámetros|datos)\) es la distribución de los parámetros que han observado los datos, conocidos como la distribución a posteriori.
• \(\Pr(datos)\) es la distribución marginal de los datos. Generalmente se obtiene integrando (o sumando) la distribución conjunta de datos y parámetros sobre los valores de los parámetros.

¿Por qué Bayes? Hay varias ventajas del enfoque bayesiano. Primero, podemos describir la distribución completa de parámetros condicionada a los datos. Esto nos permite, por ejemplo, proporcionar resultados de probabilidad con respecto a la verosimilitud de los parámetros. En segundo lugar, el enfoque bayesiano proporciona una alternativa unificada para estimar parámetros. Algunos métodos no bayesianos, como los mínimos cuadrados, requieren un enfoque separado para estimar los componentes de la varianza. Por el contrario, en los métodos bayesianos, todos los parámetros se pueden tratar de manera similar. Esto es conveniente para explicar los resultados a los usuarios del análisis de datos. Tercero, este enfoque permite a los analistas combinar información previa conocida de otras fuentes con los datos de manera coherente. Este tema se desarrolla en detalle en el capítulo de credibilidad. Cuarto, el análisis bayesiano es particularmente útil para pronosticar respuestas futuras.

Caso particular de Poisson - Gamma. Para desarrollar el método bayesiano de forma intuitiva, consideramos el caso de Poisson-Gamma que ocupa un lugar destacado en las aplicaciones actuariales. La idea es considerar un conjunto de variables aleatorias \(X_1,\ldots, X_n\), donde cada \(X_i\) podría representar el número de siniestros para el titular de la póliza i-ésima. Supongamos que \(X_i\) tiene una distribución de Poisson con parámetro \(\lambda\), análoga a la probabilidad que vimos por primera vez en el Capítulo 2. En un contexto no bayesiano (o frecuentista), el parámetro \(\lambda\) se ve como una cantidad desconocida que no es aleatoria (se dice que es “fija”). En el contexto bayesiano, el parámetro desconocido \(\lambda\) se considera incierto y se modeliza como una variable aleatoria. En este caso particular, utilizamos la distribución gamma para reflejar esta incertidumbre, la distribución a priori.

Pensemos en el siguiente esquema de muestreo en dos etapas para argumentar esta configuración probabilística.

1. En la primera etapa, el parámetro \(\lambda\) se extrae de una distribución gamma.
2. En la segunda etapa, para ese valor de \(\lambda\), hay \(n\) extracciones de la misma distribución de Poisson, que son independientes, condicionadas a \(\lambda\).

De esta configuración sencilla, surgen algunas conclusiones importantes.

• La distribución de \(X_i\) ya no es Poisson. Para el caso particular, es una distribución binomial negativa (ver el siguiente “Fragmento de teoría”).
• Las variables aleatorias \(X_1, \ldots, X_n\) no son independientes. Esto se debe a que comparten la variable aleatoria común \(\lambda\).
• Como en el contexto frecuentista, el objetivo es hacer afirmaciones sobre los valores probables de los parámetros, tales como \(\lambda\), dado los datos observados \(X_1, \ldots, X_n\). Sin embargo, debido a que ahora tanto el parámetro como los datos son variables aleatorias, podemos usar el lenguaje de probabilidad condicionada para hacer tales afirmaciones. Como veremos en la Sección 4.4.4, resulta que la distribución de \(\lambda\) dados los datos \(X_1, \ldots, X_n\) también es gamma (con parámetros actualizados), un resultado que simplifica la tarea de inferir valores probables del parámetro \(\lambda\).

Mostrar un fragmento de teoría

---

Demostremos que la distribución de \(X\) es binomial negativa. Suponemos que la distribución de \(X\) dada \(\lambda\) es Poisson, de modo que \[ \Pr(X = x|\lambda) = \frac{\lambda^x}{\Gamma(x+1)} e^{-\lambda} , \] usando la notación \(\Gamma(x+1) = x!\) para el entero \(x\). Suponga que \(\lambda\) es una extracción de una distribución gamma con parámetros fijos, por ejemplo, \(\alpha\) y \(\theta\), por lo que esto tiene pdf función de probabilidad de densidad \[ f(\lambda) = \frac{\lambda^{\alpha-1}}{\theta^{\alpha}\Gamma(\alpha)}\exp(-\lambda/\theta). \] Sabemos que una pdf integra uno. Para facilitar el desarrollo, definimos el parámetro recíproco \(\theta_r = 1/\theta\) y así tenemos \[ \int_0^{\infty} f(\lambda) ~d\lambda =1 ~~~ ==> ~~~ \theta_r^{-\alpha} \Gamma(\alpha) = \int_0^{\infty} \lambda^{\alpha-1} \exp\left(-\lambda\theta_r\right) ~ d\lambda . \] A partir del Capítulo de Apéndice 16 en esperanzas iteradas, tenemos que la pmf función masa de probabilidad de \(X\) se puede calcular de forma iterada como

\[ \begin{aligned} \Pr(X = x) &= \mathrm{E} \left\{\Pr(X = x|\lambda)\right\}\\ &= \int_0^{\infty} \Pr(X = x|\lambda) f(\lambda) ~d\lambda \\ &= \int_0^{\infty} \frac{\lambda^x}{\Gamma(x+1)} e^{-\lambda} \frac{\lambda^{\alpha-1}}{\theta^{\alpha}\Gamma(\alpha)}\exp(-\lambda/\theta) ~d\lambda\\ &= \frac{1}{\theta^{\alpha}\Gamma(x+1)\Gamma(\alpha)} \int_0^{\infty} \lambda^{x+\alpha-1} \exp\left(-\lambda(1+\frac{1}{\theta})\right) ~d\lambda \\ &= \frac{1}{\theta^{\alpha}\Gamma(x+1)\Gamma(\alpha)} \Gamma(x+\alpha)\left(1+\frac{1}{\theta}\right)^{-(x+\alpha)} \\ &= \frac{\Gamma(x+\alpha)}{\Gamma(x+1)\Gamma(\alpha)}\left(\frac{1}{1+\theta}\right)^{\alpha} \left(\frac{\theta}{1+\theta}\right)^{x} .\\ \end{aligned} \] Aquí, utilizamos la igualdad de distribución gamma con la sustitución \(\theta_r = 1+1/\theta\). Como se puede ver en la Sección2.2.3.3, ésta es una distribución binomial negativa con parámetro \(r = \alpha\) y \(\beta = \theta\).

---

En este capítulo, usamos ejemplos sencillos que se pueden hacer a mano para ilustrar los fundamentos. Para una implementación práctica, los analistas dependen en gran medida de los métodos de simulación que utilizan métodos computacionales modernos como la simulación Markov Chain Monte Carlo (MCMC). Realizaremos una introducción a las técnicas de simulación en el Capítulo 6, pero las técnicas más intensivas como MCMC requieren referencias adicionales. Ver @ hartman2016 para una introducción a los métodos bayesianos computacionales desde una perspectiva actuarial.

4.4.2 Modelo Bayesiano

Con el desarrollo intuitivo de la Sección anterior 4.4.1, ahora reformulamos el modelo bayesiano con un poco más de precisión utilizando la notación matemática. Para simplificar, este resumen supone que tanto los resultados como los parámetros son variables aleatorias continuas. En los ejemplos, a veces le pedimos al lector que aplique estos mismos principios a versiones discretas. Conceptualmente, tanto los casos continuos como los discretos son iguales; mecánicamente, uno reemplaza unpdf función de densidad de probabilidad por una pmf función masa de probabilidad y una integral por una suma.

Como se indicó anteriormente, bajo la perspectiva bayesiana, los parámetros y los datos del modelo se consideran aleatorios. Nuestra incertidumbre sobre los parámetros del proceso subyacente de generación de datos se refleja en el uso de herramientas de probabilidad.

Distribución A Priori. En concreto, pensemos en los parámetros \(\boldsymbol \theta\) como un vector aleatorio y denotemos \(\pi(\boldsymbol \theta)\) a la distribución de posibles resultados. Éste es el conocimiento que tenemos antes de que se observen los resultados y se denomina distribución a priori. Por lo general, la distribución a priori es una distribución regular y, por lo tanto, se integra o suma uno, dependiendo de si \(\boldsymbol \theta\) es continuo o discreto. Sin embargo, podemos estar muy inseguros (o no tener idea) sobre la distribución de \(\boldsymbol \theta\); la maquinaria bayesiana permite la siguiente situación \[\int \pi(\theta) d\theta = \infty, \] en cuyo caso \(\pi(\cdot)\) se denomina una impropia prior (improper prior).

Distribución del Modelo. La distribución de resultados dado un valor supuesto de \(\boldsymbol \theta\) se conoce como la distribución del modelo y se denota como \(f(x|\boldsymbol \theta) = f_{X|\boldsymbol \theta}(x|\boldsymbol \theta)\). Esta es la función habitual de masa o densidad frecuentista. Ésta es simplemente la probabilidad en el contexto frecuentista y, por lo tanto, también es conveniente usar esto como un descriptor para la distribución del modelo.

Distribución conjunta. La distribución de resultados y parámetros del modelo es, como era de esperar, conocida como la distribución conjunta y se denota como \(f(x, \boldsymbol \theta) = f(x|\boldsymbol \theta) \pi(\boldsymbol \theta)\).

Distribución marginal de resultados. La distribución de resultados puede expresarse como \[f(x) = \int f(x | \boldsymbol \theta)\pi(\boldsymbol \theta) ~d \boldsymbol \theta.\]

Esto es análogo a una distribución de mixtura frecuentista. En la distribución de la mixtura, combinamos (o “mezclamos”) diferentes subpoblaciones. En el contexto bayesiano, la distribución marginal es una combinación de diferentes realizaciones de parámetros (en algunos contextos, se puede pensar que se combinan diferentes “estados de la naturaleza”).

Distribución a posteriori de los parámetros. Después de observar los resultados (de ahí la terminología “a posteriori”), se puede usar el teorema de Bayes para escribir la distribución como \[\pi(\boldsymbol \theta | x) =\frac{f(x , \boldsymbol \theta)}{f(x)} =\frac{f(x|\boldsymbol \theta )\pi(\boldsymbol \theta)}{f(x)}\] La idea es actualizar el conocimiento de la distribución de \(\boldsymbol \theta\) (\(\pi(\boldsymbol \theta)\)) con los datos \(x\). Determinar los valores potenciales de los parámetros es un aspecto importante de la inferencia estadística.

4.4.3 Inferencia Bayesiana

4.4.3.1 Describiendo la Distribución A Posteriori de los Parámetros

Una forma de describir una distribución es mediante intervalos de confianza. Para describiri la distribución de los parámetros a posteriori, se dice que el intervalo \([a, b]\) es un intervalo de \(100(1- \alpha)\%\) de credibilidad para \(\boldsymbol \theta\) si \[\Pr(a \le \theta \le b | \mathbf{x}) \ge 1- \alpha.\]

Como alternativa, se puede realizar el análisis de decisión clásico. En esta configuración, la función de pérdida \(l(\hat{\theta}, \theta)\) determina el coste pagado por usar la estimación \(\hat{\theta}\) en lugar del verdadero \(\theta\). La estimación de Bayes es el valor que minimiza la pérdida esperada \(\mathrm{E~}[l(\hat{\theta}, \theta)]\). Algunos casos especiales importantes incluyen: \[ {\small \begin{array}{cll} \hline \text{Función de Pérdida} l(\hat{\theta}, \theta) & \text{Descripción} & \text{Estimación de Bayes } \\ \hline (\hat{\theta}- \theta)^2 & \text{Pérdida de error al cuadrado} & \mathrm{E}(\theta|X) \\ |\hat{\theta}- \theta| & \text{Pérdida de desviación absoluta} & \text{Mediana de} \pi(\theta|x) \\ I(\hat{\theta} =\theta) & \text{Pérdida cero-uno (para probabilidades discretas)} & \text{Moda de } \pi(\theta|x) \\ \hline \end{array} } \]

Minimizar la pérdida esperada es un método riguroso para proporcionar un “mejor supuesto” sobre un valor probable de un parámetro, comparable a un estimador frecuentista del parámetro desconocido (fijo).

---

Ejemplo 4.4.1. Pregunta de Examen Actuarial. Te dan:

1. En una cartera de riesgos, cada asegurado puede tener como máximo un siniestro por año.
2. La probabilidad de siniestro para un asegurado durante un año es \(q\).
3. La densidad a priori es \[\pi(q) = q^3/0,07, \ \ \ 0,6 <q <0,8\]

Un asegurado seleccionado al azar tiene un siniestro en el año 1 y cero siniestros en el año 2. Para este asegurado, calcular la probabilidad a posteriori de que \(0,7 <q <0,8\).

Mostrar solución del ejemplo

Solución. La densidad a posteriori es proporcional al producto de la función de probabilidad y la densidad a priori. Así, \[\pi(q|1,0) \propto f(1|q)\ f(0|q)\ \pi(q) \propto q(1-q)q^3 = q^4-q^5.\]

Para obtener la densidad a posteriori exacta, integramos la función anterior en su rango \((0,6, 0,8)\)

\[\int_{0,6}^{0,8} q^4-q^5 dq = \frac{q^5}{5} - \left. \frac{q^6}{6} \right|_{0,6}^{0,8} = 0,014069 \ \Rightarrow \ \pi(q|1,0)=\frac{q^4-q^5}{0,014069}.\]

Entonces \[\Pr(0,7<q<0,8|1,0)= \int_{0,7}^{0,8} \frac{q^4-q^5}{0,014069}dq = 0,5572.\]

---

Ejemplo 4.4.2. Pregunta de Examen Actuarial.

Te dan:

1. La distribución a priori del parámetro \(\Theta\) tiene una función de densidad de probabilidad: \[\pi(\theta) = \frac{1}{\theta^2}, \ \ 1 <\theta <\infty \]
2. Dado \(\Theta = \theta\), la cuantía de los siniestros sigue una distribución de Pareto con parámetros \(\alpha = 2\) y \(\theta\).

Se observa una siniestr de 3. Calcular la probabilidad a posteriori de que \(\Theta\) exceda 2.

Mostrar solución del ejemplo

Solución: La densidad a posteriori, dada una observación con valor 3 es

\[\pi(\theta|3) = \frac{f(3|\theta)\pi(\theta)}{\int_1^\infty f(3|\theta)\pi(\theta)d\theta} = \frac{\frac{2\theta^2}{(3+\theta)^3}\frac{1}{\theta^2}}{\int_1^\infty 2(3+\theta)^{-3} d\theta} = \frac{2(3+\theta)^{-3}}{\left. -(3+\theta)^{-2}\right|_1^\infty} = 32(3+\theta)^{-3}, \ \ \theta > 1.\]

Entonces

\[\Pr(\Theta>2|3) = \int_2^\infty 32(3+\theta)^{-3}d\theta = \left. -16(3+\theta)^{-2} \right|_2^\infty = \frac{16}{25} = 0,64.\]

---

4.4.3.2 Distribución Predictiva Bayesiana

Para otro tipo de inferencia estadística, a menudo es interesante “predecir” el valor de un resultado aleatorio que aún no se ha observado. En particular, para los nuevos datos \(y\), la distribución predictiva es \[f(y|x) = \int f(y|\theta)\pi(\theta | x) d \theta.\] A veces también se le llama distribución “a posteriori” ya que la distribución de los nuevos datos está condicionada a un conjunto base de datos.

Usando el error al cuadrado como la función de pérdida, la predicción bayesiana de \(Y\) es \[ \begin{aligned} \mathrm{E}(Y|X) &= \int ~y f(y|X) dy = \int y \left(\int f(y|\theta) \pi(\theta|X) d\theta \right) dy \\ &= \int \mathrm{E}(Y|\theta) \pi(\theta|X) ~d\theta . \end{aligned} \] Como se señaló anteriormente, para algunas situaciones la distribución de los parámetros es discreta, no continua. Tener un conjunto discreto de posibles parámetros nos permite pensar en ellos como “estados de la naturaleza” alternativos, lo que proporciona una interpretación útil.

---

Ejemplo 4.4.3. Pregunta de Examen Actuarial. Para una póliza en particular, las probabilidades condicionadas del número anual de siniestros, dado \(\Theta = \theta\), y la distribución de probabilidad de \(\Theta\) son las siguientes:

\[ {\small \begin{array}{l|ccc} \hline \text{Número de Siniestros} & 0 & 1 & 2 \\ \text{Probabilidad} & 2\theta & \theta & 1-3\theta \\ \hline \end{array} } \]

\[ {\small \begin{array}{l|cc} \hline \theta & 0,05 & 0,30 \\ \text{Probabilidad} & 0,80 & 0,20 \\ \hline \end{array} } \]

Se observan dos siniestros en el año 1. Calcular la predicción bayesiana del número de siniestros en el año 2.

Mostrar solución del ejemplo

Solución. Comenzamos con la distribución a posteriori del parámetro \[ \Pr(\theta|X) = \frac{\Pr(X|\theta)\Pr(\theta)}{\sum_{\theta}\Pr(X|\theta)\Pr(\theta)} \] de modo que \[ \begin{aligned} \Pr(\theta=0,05|X=2) &= \frac{\Pr(X=2|\theta=0,05)\Pr(\theta=0,05)} {\Pr(X=2|\theta=0,05)\Pr(\theta=0,05)+\Pr(X=2|\theta=0,3)\Pr(\theta=0,3)}\\ &=\frac{(1-3\times 0,05)(0,8)}{(1-3\times 0,05)(0,8)+(1-3\times 0,3)(0,2)}= \frac{68}{70}. \end{aligned} \]

Así, \(\Pr(\theta=0,3|X=1)= 1 - \Pr(\theta=0,05|X=1) = \frac{2}{70}\).

De la distribución del modelo, tenemos \[ E(X|\theta) = 0 \times 2\theta + 1 \times \theta + 2 \times (1-3\theta) = 2 - 5 \theta. \] Así,

\[ \begin{aligned} E(Y|X) &= \sum_{\theta} \mathrm{E}(Y|\theta) \pi(\theta|X) \\ &= \mathrm{E}(Y|\theta=0,05) \pi(\theta=0,05|X)+\mathrm{E}(Y|\theta=0,3) \pi(\theta=0,3|X)\\ &= ( 2 - 5 (0,05))\frac{68}{70} + ( 2 - 5 (0,3))\frac{2}{70} = 1,714. \end{aligned} \]

---

Ejemplo 4.4.4. Pregunta de Examen Actuarial.

Te dan:

1. Las pérdidas de las pólizas de seguro de una compañía siguen una distribución de Pareto con función de densidad de probabilidad: \[ f(x | \theta) = \frac{\theta}{(x + \theta)^2}, \ \ 0 <x <\infty \]
2. Para la mitad de las pólizas de la compañía \(\theta = 1\), mientras que para la otra mitad \(\theta = 3\).

Para una póliza seleccionada al azar, las pérdidas en el año 1 fueron 5. Calcular la probabilidad a posteriori de que las pérdidas para esta póliza en el año 2 excedan de 8.

Mostrar solución del ejemplo

Solución.

Se nos da la distribución a priori de \(\theta\) como \(\Pr(\theta = 1) = \Pr(\theta = 3) = \frac{1}{2}\), la distribución condicional \(f (x | \theta)\), y el hecho de que observamos \(X_1 = 5\). El objetivo es encontrar la probabilidad predictiva \(\Pr(X_2> 8 | X_1 = 5)\).

Las probabilidades a posteriori son

\[ \begin{aligned} \Pr(\theta=1|X_1=5) &= \frac{f(5|\theta=1)\Pr(\theta=1)}{f(5|\theta=1)\Pr(\theta=1) + f(5|\theta=3)\Pr(\theta=3)} \\ &= \frac{\frac{1}{36}(\frac{1}{2})}{\frac{1}{36}(\frac{1}{2})+\frac{3}{64}(\frac{1}{2})} = \frac{\frac{1}{72}}{\frac{1}{72} + \frac{3}{128}} = \frac{16}{43} \end{aligned} \]

\[ \begin{aligned} \Pr(\theta=3|X_1=5) &= \frac{f(5|\theta=3)\Pr(\theta=3)}{f(5|\theta=1)\Pr(\theta=1) + f(5|\theta=3)\Pr(\theta=3)} \\ &= 1-\Pr(\theta=1|X_1=5) = \frac{27}{43} \end{aligned} \]

Tener en cuenta que la probabilidad condicionada de que las pérdidas excedan de 8 es \[ \begin{aligned} \Pr(X_2>8|\theta) &= \int_8^\infty f(x|\theta)dx \\ &= \int_8^\infty \frac{\theta}{(x+\theta)^2}dx = \left. -\frac{\theta}{x+\theta} \right|_8^\infty = \frac{\theta}{8 + \theta} \end{aligned} \]

La probabilidad predictiva es, por lo tanto,

\[ \begin{aligned} \Pr(X_2>8|X_1=5) &= \Pr(X_2>8|\theta=1) \Pr(\theta=1|X_1=5) + \Pr(X_2>8|\theta=3) \Pr(\theta=3 | X_1=5) \\ &= \frac{1}{8+1}\left( \frac{16}{43}\right) + \frac{3}{8+3} \left( \frac{27}{43}\right) = 0,2126 \end{aligned} \]

---

Ejemplo 4.4.5. Pregunta de Examen Actuarial.

Te dan:

1. La probabilidad de que un asegurado tenga al menos una pérdida durante cualquier año es \(p\).
2. La distribución a priori de \(p\) es uniforme en \([0, 0,5]\).
3. Se observa a un asegurado durante 8 años y tiene al menos una pérdida cada año.

Calcular la probabilidad a posteriori de que el asegurado tenga al menos una pérdida durante el Año 9.

Mostrar solución del ejemplo

Solución. La densidad de probabilidad a posteriori es\[ \begin{aligned} \pi(p|1,1,1,1,1,1,1,1) &\propto \Pr(1,1,1,1,1,1,1,1|p)\ \pi(p) = p^8(2) \propto p^8 \\ \Rightarrow \pi(p|1,1,1,1,1,1,1,1) &= \frac{p^8}{\int_0^5 p^8 dp} = \frac{p^8}{(0,5^9)/9} = 9(0,5^{-9})p^8 \end{aligned} \]

Por lo tanto, la probabilidad a posteriori de que el asegurado tenga al menos una pérdida durante el Año 9 es

\[ \begin{aligned} \Pr(X_9=1|1,1,1,1,1,1,1,1) &= \int_0^5 \Pr(X_9=1|p) \pi(p|1,1,1,1,1,1,1,1) dp \\ &= \int_0^5 p(9)(0,5^{-9})p^8 dp = 9(0,5^{-9})(0,5^{10})/10 = 0,45 \end{aligned} \]

---

Ejemplo 4.4.6. Pregunta de Examen Actuarial. Te dan:

1. Cada riesgo tiene como máximo una reclamación cada año.\[ {\small \begin{array}{ccc} \hline \text{Tipo de Riesgo } & \text{Probabilidad A Priori } & \text{Probabilidad Anual de Reclamación } \\ \hline \text{I} & 0,7 & 0,1 \\ \text{II} & 0,2 & 0,2 \\ \text{III} & 0,1 & 0,4 \\ \hline \end{array} } \]

Un riesgo elegido al azar tiene tres reclamaciones durante los años 1-6. Calcular la probabilidad a posteriori de una reclamación por este riesgo en el año 7.

Mostrar solución del ejemplo

Solución. Las probabilidades son de una distribución binomial con 6 ensayos en los que se observaron 3 sucesos.

\[ \begin{aligned} \Pr(3|\text{I}) &= {6 \choose 3} (0,1^3)(0,9^3) = 0,01458 \\ \Pr(3|\text{II}) &= {6 \choose 3} (0,2^3)(0,8^3) = 0,08192 \\ \Pr(3|\text{III}) &= {6 \choose 3} (0,4^3)(0,6^3) = 0,27648 \end{aligned} \]

La probabilidad de observar tres sucesos es \[ \begin{aligned} \Pr(3) &= \Pr(3|\text{I})\Pr(\text{I}) + \Pr(3|\text{II})\Pr(\text{II}) + \Pr(3|\text{III})\Pr(\text{III}) \\ &= 0,7(0,01458) + 0,2(0,08192) + 0,1(0,27648) = 0,054238 \end{aligned} \]

Las tres probabilidades a posteriori son \[ \begin{aligned} \Pr(\text{I}|3) &= \frac{\Pr(3|\text{I})\Pr(\text{I})}{\Pr(3)} = \frac{0,7(0,01458)}{0,054238} = 0,18817 \\ \Pr(\text{II}|3) &= \frac{\Pr(3|\text{II})\Pr(\text{II})}{\Pr(3)} = \frac{0,2(0,08192)}{0,054238} = 0,30208 \\ \Pr(\text{III}|3) &= \frac{\Pr(3|\text{III})\Pr(\text{III})}{\Pr(3)} = \frac{0,1(0,27648)}{0,054238} = 0,50975 \end{aligned} \]

La probabilidad a posteriori de una reclamación es, entonces, \[ \begin{aligned} \Pr(\text{siniestro} | 3) &= \Pr(\text{claim}|\text{I})\Pr(\text{I} | 3) + \Pr(\text{siniestro} | \text{II})\Pr(\text{II} | 3) + \Pr(\text{siniestro} | \text{III}) \Pr(\text{III} | 3) \\ &= 0,1(0,18817) + 0,2(0,30208) + 0,4(0,50975) = 0,28313 \end{aligned} \]

---

4.4.4 Distribuciones Conjugadas

En el marco bayesiano, la clave para la inferencia estadística es comprender la distribución a posteriori de los parámetros. Como se describe en la Sección @ref(S: IntroBayes), el análisis de datos basado en métodos bayesianos utiliza técnicas computacionalmente intensivas como simulación MCMC Markov Chain Monte Carlo. Otro enfoque para calcular distribuciones a posteriori se basa en distribuciones conjugadas. Aunque este enfoque está disponible solo para un número limitado de distribuciones, tiene el atractivo de que proporciona expresiones de forma cerrada para las distribuciones, lo que permite una fácil interpretación de los resultados.

Para relacionar las distribuciones a priori y a posteriori de los parámetros, tenemos la relación

\[ \begin{array}{ccc} \pi(\boldsymbol \theta | x) & = & \frac{f(x|\boldsymbol \theta )\pi(\boldsymbol \theta)}{f(x)} \\ & \propto & f(x|\boldsymbol \theta ) \pi(\boldsymbol \theta) \\ \text{a posteriori} & \text{es proporcional a} & \text{verosimilitud} \times \text{a priori} . \end{array} \]

Para distribuciones conjugadas, la a posteriori y la a priori provienen de la misma familia de distribuciones. La siguiente ilustración analiza el caso particular de Poisson-gamma, el más conocido en aplicaciones actuariales.

Caso Particular – Poisson-Gamma - Continuación. Supongamos una distribución de modelo de Poisson(\(\lambda\)) y que \(\lambda\) siga una distribución a priori gamma(\(\alpha, \theta\)). En este caso, la distribución a posteriori de \(\lambda\) dados los datos sigue una distribución gamma con nuevos parámetros \(\alpha_{post} = \sum_i x_i + \alpha\) y \(\theta_{post} = 1/(n + 1 /\theta)\).

Mostrar detalles del caso particular

Caso Particular – Poisson-Gamma – Continuación. La distribución del modelo es \[f(\mathbf{x} | \lambda) = \prod_{i=1}^n \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} .\]

La distribución a priori es

\[\pi(\lambda) = \frac{\left(\lambda/\theta\right)^{\alpha} \exp(-\lambda/\theta)}{\lambda \Gamma(\alpha)}.\] Por lo tanto, la distribución a posteriori es proporcional a \[ \begin{aligned} \pi(\lambda | \mathbf{x}) &\propto f(\mathbf{x}|\theta ) \pi(\lambda) \\ &= C \lambda^{\sum_i x_i + \alpha -1} \exp(-\lambda(n+1/\theta)) \end{aligned} \]

donde \(C\) es una constante. Se aprecia que se trata de una distribución gamma con nuevos parámetros \(\alpha_{post} = \sum_i x_i + \alpha\) y \(\theta_{post} = 1/(n + 1/\theta)\). Por lo tanto, la distribución gamma es una conjugada a priori para la distribución del modelo de Poisson.

---

Ejemplo 4.4.7. Pregunta de Examen Actuarial.

Te dan:

1. La distribución condicionada del número de siniestros por titular de la póliza es una Poisson con un promedio de \(\lambda\).
2. La variable \(\lambda\) tiene una distribución gamma con los parámetros \(\alpha\) y \(\theta\).
3. Para los asegurados con 1 siniestro en el Año 1, la predicción de Bayes para el número de siniestros en el Año 2 es 0,15.
4. Para los asegurados con un promedio de 2 siniestros por año en el año 1 y en el año 2, la predicción de Bayes para el número de siniestros en el año 3 es de 0,20.

Calcular \(\theta\).

Mostrar solución del ejemplo

Solución.

Dado que la distribución condicionada del número de siniestros por asegurado, \(E(X | \lambda) = Var(X | \lambda) = \lambda\), la predicción de Bayes es

\[ \begin{aligned} \mathrm{E}(X_2|X_1) &= \int \mathrm{E}(X_2|\lambda) \pi(\lambda|X_1) d\lambda = \alpha_{new} \theta_{new} \end{aligned} \] porque la distribución a posteriori es gamma con parámetros \(\alpha_{new}\) y \(\theta_{new}\).

Para el año 1, tenemos \[ 0,15 = (X_1 + \alpha) \times \frac{1}{n+1/\theta} = (1 + \alpha) \times \frac{1}{1+1/\theta}, \] de modo que \(0,15(1+1/\theta)= 1 + \alpha\). Para el año 2, tenemos \[ 0,2 = (X_1+X_2 + \alpha) \times \frac{1}{n+1/\theta} = (4 + \alpha) \times \frac{1}{2+1/\theta}, \] de modo que \(0,2(2+1/\theta)= 4 + \alpha\). Igualando estos resultados \[ 0,2(2+1/\theta)=3 + 0,15(1+1/\theta) \] resulta que \(\theta = 1/55 = 0,018182\).

---

Las expresiones de forma cerrada significan que los resultados se pueden interpretar y calcular fácilmente; por lo tanto, las distribuciones conjugadas son útiles en la práctica actuarial. Otros dos casos especiales utilizados ampliamente son:

• La incertidumbre de los parámetros se describe mediante una distribución beta y los resultados tienen una distribución binomial (condicionada al parámetro).
• La incertidumbre de los parámetros se describe mediante una distribución normal y los resultados se distribuyen condicionalmente como normales.

Resultados adicionales sobre las distribuciones conjugadas se resumen en la Sección del Apéndice 16.3.

4.5 Más Recursos y Colaboradores

Ejercicios

Aquí hay un conjunto de ejercicios que guían al lector a través de algunos de los fundamentos teóricos de Análisis de la Función de Pérdida. Cada tutorial se basa en una o más preguntas de los exámenes actuariales profesionales, generalmente el Examen C de la Sociedad de Actuarios.

Tutoriales guiados de Selección de Modelo

Autores

• Edward W. (Jed) Frees y Lisa Gao, University of Wisconsin-Madison, son los principales autores de la versión inicial de este capítulo. Email: jfrees@bus.wisc.edu para comentarios sobre el capítulo y sugerencias de mejora.
• Los revisores del capítulo incluyen: Andrew Kwon-Nakamura, Hirokazu (Iwahiro) Iwasawa, Eren Dodd.
• Traducción al español: Catalina Bolancé (Universitat de Barcelona).