Chapter 14 Modelización de la Dependencia
Chapter Preview. En la práctica, hay muchos tipos de variables que uno podría encontrar y el primer paso en la modelización de la dependencia es identificar el tipo de variable con el que se está tratando con el objetivo de identificar la técnica adecuada. Este capítulo presenta a los lectores los tipos de variables y las técnicas para modelizar la dependencia o asociación de distribuciones multivariantes. La sección 14.1 proporciona una descripción general de los tipos de variables. Posteriormente, la sección 14.2 describe las medidas básicas para medir la dependencia entre variables.
La Sección 14.3 presenta un enfoque novedoso para modelizar la dependencia mediante Cópulas, que se refuerza con ilustraciones prácticas en la Sección 14.4. Los tipos de familias de Copula y las propiedades básicas de las funciones de Copula se explican en la Sección 14.5. El capítulo concluye explicando por qué es importante el estudio de la modelización de la dependencia en la Sección 14.6.
14.1 Tipos de Variables
En esta sección aprenderemos como:
- Clasificar las variables como cualitativas o cuantitativas.
- Describir el comportamiento multivariante de las variables.
Las personas, las empresas y otras entidades que queremos comprender se describen a partir de un conjunto de datos mediante características numéricas. Como estas características varían según la entidad, se conocen comúnmente como variables. Para la gestión de las entidades de seguros, será fundamental comprender la distribución de cada variable y cómo éstas se asocian entre sí. Es común que los conjuntos de datos tengan muchas variables (elevada dimensión), por lo que es útil comenzar clasificándolos en diferentes tipos. Como se verá, estas clasificaciones no son estrictas; hay superposición entre los grupos. No obstante, el agrupamiento resumido en la Tabla 14.1 y explicado en el resto de esta sección proporciona un sólido primer paso para enmarcar un conjunto de datos.
\[ {\small \begin{matrix} \begin{array}{l|l} \hline \textbf{Tipo de Variable} & \textbf{Ejemplo} \\\hline Cualitativa & \\ \text{Binaria} & \text{Sexo} \\ \text{Categórica (No ordenada, Nominal)} & \text{Territorio (ejemplo, estado/provincia) en la que el asegurado reside } \\ \text{Categórica Ordenada (Ordinal)} & \text{Satisfacción del Reclamante (cinco valores en una escala entre 1=insatisfecho } \\ & ~~~ \text{y 5 =satisfecho)} \\\hline Cuantitativa & \\ \text{Continua} & \text{Edad, peso, renta del asegurado} \\ \text{Discreta} & \text{Cuantía de la franquicia (0, 250, 500, and 1000)} \\ \text{Conteo} & \text{Número de siniestros del asegurado} \\ \text{Combinaciones de} & \text{Pérdidas de la póliza, mezclada con 0 (para las no pérdidas)} \\ ~~~ \text{Discreta y Continua} & ~~~\text{y cuantía de la reclamación positiva} \\ \text{Variable de Intervalo} & \text{Edad el Conductor: 16-24 (joven), 25-54 (intermedia),} \\ & ~~~\text{55 y más (senior)} \\ \text{Datos Circulares} & \text{Hora del día de llegada del cliente} \\ \hline Multivariante ~ Variable & \\ \text{Datos de Gran Dimensión} & \text{ Características de una empresa que compra compensación de trabajadores} \\ & ~~~\text{seguro (ubicación de las plantas, industria, número de empleados} \\ &~~~\text{y así)} \\ \text{Datos Espaciales } & \text{Longitud/latitud de la ubicación de una reclamación de un seguro por granizo} \\ \text{Datos Ausentes (Missing)} & \text{ Edad del titular de la póliza (continua/intervalo) y "-99" para } \\ &~~~ \text{"no reportado," esto es, missing} \\ \text{Datos Censurados y Truncados } & \text{Importe de las reclamaciones de seguros que exceden una franquicia} \\ \text{Reclamaciones Agregadas} & \text{Pérdidas registradas para cada siniestro en una póliza de vehículos de motor.} \\ \text{Realizaciones de Procesos Estocásticos } & \text{ El tiempo y el importe de cada ocurrencia de una pérdida asegurada} \\ \hline \end{array} \end{matrix}} \]
Tabla 14.1 : Tipos de Variables
En el análisis de datos, es importante comprender con qué tipo de variable se está trabajando. Por ejemplo, considere un par de variables aleatorias (Coverage,Claim) (Cobertura,Reclamación) de los datos LGPIF presentados en el capítulo 1 como se muestra posteriormente en la Figura 14.1. Nos gustaría saber si la distribución de Coverage depende de la distribución de Claim o si son estadísticamente independientes. También nos gustaría saber cómo depende la distribución de Claim de la variable EntityType. Debido a que la variable EntityType pertenece a una clase diferente de variables, modelizar la dependencia entre Claim y Coverage puede requerir una técnica diferente a la de Claim y EntityType.
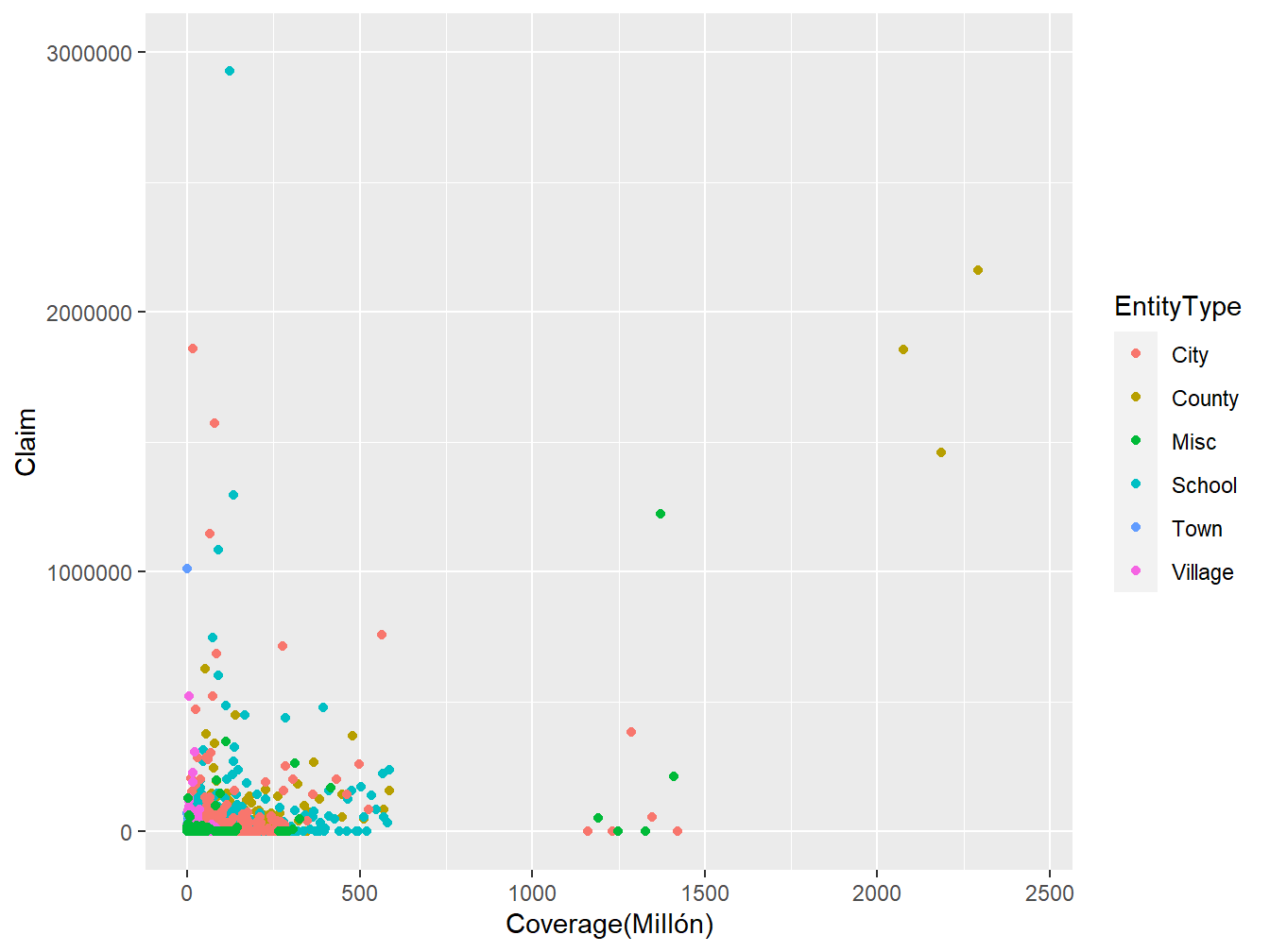
Figure 14.1: Gráfico de dispersión de (Coverage,Claim) utilizando los datos LGPIF
14.1.1 Variables Cualitativas
En esta subsección aprenderemos como:
- Clasificar las variables cualitativas como nominales y ordinales
- Describir las variables binarias
Una variable cualitativa o categórica es una variable en la que la medida denota pertenencia a un conjunto de grupos o categorías. Por ejemplo, si se estuviera codificando en qué área del país reside un asegurado, se podría usar un 1 para la parte norte, 2 para el sur y 3 para todo lo demás. Esta variable de ubicación es un ejemplo de variable nominal, para la cual los niveles no tienen un orden natural. Cualquier análisis de variables nominales no debe depender del etiquetado de las categorías. Por ejemplo, en lugar de usar 1,2,3 para norte, sur, otro, debería llegar al mismo conjunto de estadísticos descriptivos si se usara una codificación 2,1,3, intercambiando norte y sur. Por el contrario, una variable ordinal es un tipo de variable categórica para la que existe un orden. Por ejemplo, con una encuesta para ver qué tan satisfechos están los clientes con nuestro departamento de atención de reclamaciones, podríamos usar una escala de cinco puntos que va desde 1 que significa insatisfecho hasta 5 que significa satisfecho. Las variables ordinales proporcionan un orden claro de los niveles de una variable, pero se desconoce la cuantía de separación entre los niveles.
Una variable binaria es un tipo especial de variable categórica donde solo hay dos categorías comúnmente identificadas como 0 y 1. Por ejemplo, podríamos codificar una variable en un conjunto de datos para que sea 1 si un asegurado es mujer y un 0 si es hombre.
14.1.2 Variables Cuantitativas
En esta subsección aprenderemos como:
- Diferenciar entre variable continua y discreta
- Usar una combinación de variables continuas y discretas
- Describir los datos circulares
A diferencia de una variable cualitativa, una variable cuantitativa es aquella en la que el nivel numérico es una realización de alguna escala, de modo que la distancia entre dos niveles cualquiera de la escala adquiere significado. Una variable continua es aquella que puede tomar cualquier valor dentro de un intervalo finito. Por ejemplo, es común representar la edad, el peso o los ingresos de un asegurado como una variable continua. Por el contrario, una variable discreta es aquella que toma solo un número finito de valores en cualquier intervalo finito. Por ejemplo, al examinar la elección de deducibles de un titular de póliza, puede ser que los valores de 0, 250, 500 y 1000 sean los únicos resultados posibles. Como una variable ordinal, estos representan categorías distintas que están ordenadas. A diferencia de una variable ordinal, la diferencia numérica entre niveles adquiere un significado económico. Un tipo especial de variable discreta es variable de conteo, que toma valores en los enteros no negativos. Por ejemplo, nos interesará especialmente el número de siniestros derivados de una póliza durante un período determinado.
Algunas variables son inherentemente una combinación de componentes discretos y continuos. Por ejemplo, cuando analizamos la pérdida de un asegurado, encontraremos un resultado discreto en el cero, que representa que no hay pérdida, y un conjunto de valores continuos correspondientes a los resultados positivos, que representa la cuantía de la pérdida asegurada. Otra variación interesante es variable de intervalo, que da un rango de resultados posibles.
Datos circulares representan una interesante categoría de variables que normalmente no se analiza en asegurados. Como ejemplo de datos circulares, suponga que supervisa las llamadas a su centro de servicio al cliente y le gustaría saber cuándo es la hora pico del día para recibir llamadas. En este contexto, uno puede pensar en la hora del día como una variable con realizaciones en un círculo, por ejemplo, imagine una imagen analógica de un reloj. Para datos circulares, la distancia entre las observaciones a las 00:15 y las 00:45 es tan cercana como entre las observaciones a las 23:45 y las 00:15 (aquí, usamos la nomenclatura HH:MM que significa horas y minutos).
14.1.3 Variables Multivariantes
En esta subsección aprenderemos como:
- Diferenciar entre datos univariantes y multivariantes
- Manejar variables ausentes (missing)
Los datos de seguros suelen ser multivariantes en el sentido de que podemos disponer de muchas medidas para una sola entidad. Por ejemplo, al estudiar las pérdidas asociadas con el plan de indemnización de los trabajadores de una empresa, es posible que queramos saber la ubicación de sus plantas de fabricación, la industria en la que opera, el número de empleados, etc. La estrategia habitual para analizar datos multivariantes es comenzar examinando cada variable aisladamente de las demás. Esto se conoce como enfoque univariante.
Por el contrario, para algunas variables, tiene poco sentido mirar solo aspectos unidimensionales. Por ejemplo, las aseguradoras suelen organizar datos espaciales por longitud y latitud para analizar la ubicación de las reclamaciones de seguros relacionadas con el clima y debidas a tormentas de granizo. Tener un solo número, ya sea de longitud o latitud, proporciona poca información para comprender la ubicación geográfica.
Otro caso especial de una variable multivariante, que es menos obvio, involucra la codificación de datos ausentes. Históricamente, algunos paquetes estadísticos usaban un -99 para informar cuando una variable, como la edad del titular de la póliza, no estaba disponible o no se informaba. Esto llevó a muchos analistas desprevenidos a proporcionar estadísticas extrañas al resumir un conjunto de datos. Cuando faltan datos, es mejor pensar en la variable como dos dimensiones, una para indicar si la variable se informa o no y la segunda proporciona la edad (si se informa). De la misma manera, los datos de seguros son comúnmente censurados y truncados. Le remitimos al Capítulo 4 para obtener más información sobre datos censurados y truncados. Siniestros agregados también se pueden codificar como otro tipo especial de variable multivariante. Le remitimos al Capítulo 5 para obtener más información sobre Reclamaciones Agregadas.
Quizás el tipo más complicado de variable multivariante es la que se obtiene de la realización de un proceso estocástico. Recordará que un proceso estocástico es poco más que una colección de variables aleatorias. Por ejemplo, en seguros, podríamos pensar en las veces que llegan los siniestros a una compañía de seguros en un horizonte temporal de un año. Esta es una variable de alta dimensión que teóricamente es infinitamente dimensional. Se requieren técnicas especiales para comprender las realizaciones de los procesos estocásticos que no se abordarán aquí.
14.2 Medidas clásicas de asociaciones escalares
En esta subsección aprenderemos como:
- Estimar la correlación usando el método de Pearson
- Usar las medidas basadas en rangos como Spearman y Kendall para estimar la correlación
- Medir la dependencia usando odds-ratio, la Chi-cuadrado de Pearson y el estadístico para el contraste de cociente de verosimilitud
- Usar la correlación basada en la normal para cuantificar la asociación entre variables ordinales
14.2.1 Medidas de Asociación para Variables Ordinales
Para esta sección, considere un par de variables aleatorias \((X,Y)\) que tienen una función de distribución conjunta \(F(\cdot)\) y una muestra aleatoria \((X_i,Y_i), i=1, \ldots, n\). Para el caso continuo, suponga que \(F(\cdot)\) es absolutamente continua con marginales absolutamente continuas.
14.2.1.1 Correlación de Pearson
Se define la función de covarianza muestral \(\widehat{Cov}(X,Y)=\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})\), donde \(\bar{X}\) y \(\bar{Y}\) son las medias muestrales de \(X\) y \(Y\), respectivamente. Entonces, correlación producto-momento (Pearson) se puede escribir como
\[\begin{equation*} r = \frac{\widehat{Cov}(X,Y)}{\sqrt{\widehat{Cov}(X,X)\widehat{Cov}(Y,Y)}}. \end{equation*}\]
El estadístico de correlación \(r\) se usa ampliamente para capturar la asociación lineal entre variables aleatorias. Es un estimador (no paramétrico) del parámetro de correlación \(\rho\), definido como la covarianza dividida por el producto de las desviaciones estándares. En este sentido, captura la asociación entre cualquier par de variables aleatorias.
Este estadístico tiene varias características importantes. A diferencia de los estimadores para la regresión, es simétrico entre variables aleatorias, por lo que la correlación entre \(X\) y \(Y\) es igual a la correlación entre \(Y\) y \(X\). No se modifica mediante transformaciones lineales de las variables aleatorias (hasta con cambios de signo) por lo que podamos multiplicar variables aleatorias o agregar constantes según sea útil para la interpretación. El rango del estadístico es \([-1,1]\), que no depende de la distribución de \(X\) o \(Y\).
Además, en el caso de la independencia, el coeficiente de correlación \(r\) es 0. Sin embargo, es bien sabido que la correlación cero no implica independencia, excepto para variables aleatorias normalmente distribuidas. El estadístico de correlación \(r\) también es un estimador (de máxima verosimilitud) del parámetro de asociación para la distribución normal bivariante. Entonces, para datos normalmente distribuidos, el estadístico de correlación \(r\) puede usarse para evaluar la independencia. Para interpretaciones adicionales de este conocido estadístico, los lectores disfrutarán con (Lee Rodgers and Nicewander 1998).
Puede obtener el estadístico Correlación de Pearson \(r\) usando la función cor() en R y seleccionando el método pearson. Esto se demuestra a continuación mediante el uso de la variable de valoración de Coverage en millones de dólares y la variable de cuantía de Claim en dólares de los datos de LGPIF presentados en el capítulo 1.
Código R para el Estadístico de Correlación de Pearson
A partir del output de R anterior, \(r=0,31\) , que indica una asociación positiva entre Claim y Coverage. Esto significa que cuando la cantidad de cobertura de la póliza aumenta esperamos que la cuantía del siniestro aumente.
14.2.2 Medidas Basadas en Rangos
14.2.2.1 Rho de Spearman
El coeficiente de correlación de Pearson tiene el inconveniente de que no es invariable a las transformaciones no lineales de los datos. Por ejemplo, la correlación entre \(X\) y \(\ln Y\) puede ser bastante diferente de la correlación entre \(X\) y \(Y\). Como vemos en el código R para el estadístico de correlación de Pearson anterior, el estadístico de correlación \(r\) entre la variable de valoración de Coverage en logaritmos de millones de dólares y la variable de cuantía de Claim en dólares es \(0,1\) en comparación con \(0,31\) que se obtiene cuando se calcula la correlación entre la variable de valoración de Coverage en millones de dólares y la variable de cuantía de Claim en dólares. Esta limitación es una razón para considerar estadísticos alternativos.
Las medidas alternativas de correlación se basan en los rangos de los datos. Sea \(R(X_j)\) el rango de \(X_j\) de la muestra \(X_1, \ldots, X_n\) y de manera similar para \(R(Y_j)\). Sea \(R(X) = \left(R(X_1), \ldots, R(X_n)\right)'\) el vector de rangos, y de manera similar para \(R(Y)\). Por ejemplo, si \(n=3\) y \(X=(24, 13, 109)\), entonces \(R(X)=(2,1,3)\). Se puede encontrar una introducción completa de los estadísticos de rango, por ejemplo, en (Hettmansperger 1984). Además, los rangos se pueden utilizar para obtener la función de distribución empírica; consulte la sección 4.1.1 para obtener más información sobre la función de distribución empírica.
Con esto, la medida de correlación de (Spearman 1904) es simplemente la correlación producto-momento calculada con los rangos: \[\begin{equation*} r_S = \frac{\widehat{Cov}(R(X),R(Y))}{\sqrt{\widehat{Cov}(R(X),R(X))\widehat{Cov}(R(Y),R(Y))}} = \frac{\widehat{Cov}(R(X),R(Y))}{(n^2-1)/12} . \end{equation*}\]
Puede obtener el estadístico de correlación de Spearman \(r_S\) utilizando la función cor() en R y seleccionando el método spearman. Como se observa más abajo, la correlación de Spearman entre la variable de valoración de Coverage en millones de dólares y la variable de cuantía de Claim en dólares es de \(0,41\).
Código R para el Estadístico de Correlación de Spearman
Podemos demostrar que el estadístico de correlación de Spearman es invariante bajo transformaciones estrictamente crecientes. Del código R para el estadístico de correlación de Spearman anterior entre la variable de valoración de Coverage en logaritmos de millones de dólares y la variable de cuantía de Claim en dólares se obtiene \(r_S=0,41\).
14.2.2.2 Tau de Kendall
Una medida alternativa que utiliza rangos se basa en el concepto de concordance (concordancia). Se dice que un par de observaciones \((X,Y)\) es concordante (discordante) si la observación con un valor mayor de \(X\) también tiene el mayor (menor) valor de \(Y\). Entonces \(\Pr(concordancia) = \Pr[ (X_1-X_2)(Y_1-Y_2) >0 ]\) , \(\Pr(discordancia) = \Pr[ (X_1-X_2)(Y_1-Y_2) <0 ]\) , \(\Pr(empate) = \Pr[ (X_1-X_2)(Y_1-Y_2) =0 ]\) y
\[\begin{eqnarray*} \tau(X,Y)= \Pr(concordance) - \Pr(discordance) = 2\Pr(concordance) - 1 + \Pr(tie). \end{eqnarray*}\]
Para estimar esto, se dice que los pares \((X_i,Y_i)\) y \((X_j,Y_j)\) son concordantes si el producto \(sgn(X_j-X_i)sgn(Y_j-Y_i)\) es igual a 1 y discordantes si el mismo producto es igual a -1. Aquí, \(sgn(x)=1,0,-1\) como \(x>0\), \(x=0\), \(x<0\), respectivamente. Con esto, podemos expresar la medida de asociación de (Maurice G. Kendall 1938), conocida como Kendall’s tau, como
\[\begin{equation*} \begin{array}{rl} \tau &= \frac{2}{n(n-1)} \sum_{i<j}sgn(X_j-X_i)sgn(Y_j-Y_i)\\ &= \frac{2}{n(n-1)} \sum_{i<j}sgn(R(X_j)-R(X_i))sgn(R(Y_j)-R(Y_i)) \end{array}. \end{equation*}\]
Curiosamente, (Hougaard 2000), página 137, atribuye el descubrimiento original de este estadístico a (Fechner 1897) y señala que el descubrimiento de Kendall fue independiente y más completo que el trabajo original.
Puedes obtener la tau de Kendall usando la función cor() en R y seleccionando el método kendall. Como se observa más abajo, la Tau de Kendall entre la variable de valoración de Coverage en millones de dólares y la variable de cuantía de Claim en dólares es \(\tau=0,32\). Cuando hay empates en los datos, la función cor() calcula Tau_b de Kendall, como propone (M. G. Kendall 1945).
Código R para la Tau de Kendall
Además, para mostrar que la tau de Kendall es invariable bajo transformaciones estrictamente crecientes, entre la variable de valoración de Coverage en logaritmos de millones de dólares y la variable de cuantía de Claim en dólares es \(\tau=0,32\).
14.2.3 Variables Nominales
14.2.3.1 Variables Bernoulli
Para analizar por qué las medidas de dependencia para variables continuas pueden no ser las mejores para variables discretas, centrémonos en el caso de las variables de Bernoulli que toman valores binarios simples, 0 y 1. Se define la notación, sea \(\pi_{jk} = \Pr(X=j, Y=k)\) para \(j,k=0,1\) y sea \(\pi_X=\Pr(X=1)\) y similarmente para \(\pi_Y\). Entonces, se puede ver fácilmente que la versión poblacional de la correlación producto-momento (Pearson) es \[\begin{eqnarray*} \rho = \frac{\pi_{11} - \pi_X \pi_Y}{\sqrt{\pi_X(1-\pi_X)\pi_Y(1-\pi_Y)}} . \end{eqnarray*}\]
A diferencia del caso de los datos continuos, no es posible que esta medida alcance los límites del intervalo \([-1,1]\). Para ver esto, los estudiantes de probabilidad pueden recordar los límites de Fr\(\acute{e}\)chet-H\(\ddot{o}\)effding para una distribución conjunta, que resultan ser \(\max\{0, \pi_X+\pi_Y -1\} \le \pi_{11} \le \min\{\pi_X,\pi_Y\}\) para esta probabilidad conjunta. Este límite de la probabilidad conjunta impone una restricción adicional a la correlación de Pearson. Como ilustración, suponga probabilidades iguales \(\pi_X =\pi_Y = \pi > 1/2\). Entonces, el límite inferior es
\[\begin{eqnarray*} \frac{2\pi - 1 - \pi^2}{\pi(1-\pi)} = -\frac{1-\pi}{\pi} . \end{eqnarray*}\]
Por ejemplo, si \(\pi=0,8\), entonces lo menor que podría ser la correlación de Pearson es -0,25. Más generalmente, hay límites en \(\rho\) que dependen de \(\pi_X\) y \(\pi_Y\) que dificultan la interpretación de esta medida.
Como señaló (Y. M. Bishop, Fienberg, and Holland 1975) (página 382), elevar al cuadrado este coeficiente de correlación produce la estadística Chi-cuadrado de Pearson (presentada en el capítulo 2). A pesar de los problemas de límites descritos anteriormente, esta característica hace que el coeficiente de correlación de Pearson sea una buena opción para describir la dependencia con datos binarios. La otra opción es el odds ratio, que se describe a continuación.
Como medida alternativa para las variables de Bernoulli, el odds ratio viene dado por:
\[\begin{eqnarray*} OR(\pi_{11}) = \frac{\pi_{11} \pi_{00}}{\pi_{01} \pi_{10}} = \frac{\pi_{11} \left( 1+\pi_{11}-\pi_X -\pi_Y\right)}{(\pi_X-\pi_{11})(\pi_Y- \pi_{11})} . \end{eqnarray*}\]
Cálculos agradables muestran que \(OR(z)\) es \(0\) en el límite inferior Fr\(\acute{e}\)chet-H\(\ddot{o}\)effding \(z= \max\{0, \pi_X+\pi_Y- 1\}\) y es \(\infty\) en el límite superior \(z=\min\{\pi_X,\pi_Y\}\). Por lo tanto, los límites de esta medida no dependen de las probabilidades marginales \(\pi_X\) y \(\pi_Y\), lo que facilita su interpretación.
Como señaló (Yule 1900), los odds ratios son invariantes al etiquetado de 0 y 1. Además, son invariantes a las marginales en el sentido de que se puede rescalar \(\pi_X\) y \(\pi_Y\) mediante constantes positivas y los odds ratios se mantiene sin cambios. Específicamente, suponga que \(a_i\), \(b_j\) son conjuntos de constantes positivas y que
\[\begin{eqnarray*} \pi_{ij}^{new} &=& a_i b_j \pi_{ij} \end{eqnarray*}\] y \(\sum_{ij} \pi_{ij}^{new}=1.\) Entonces, \[\begin{eqnarray*} OR^{new} = \frac{(a_1 b_1 \pi_{11})( a_0 b_0 \pi_{00})}{(a_0 b_1 \pi_{01})( a_1 b_0\pi_{10})} = \frac{\pi_{11} \pi_{00}}{\pi_{01} \pi_{10}} =OR^{old} . \end{eqnarray*}\]
Para obtener ayuda adicional con la interpretación, Yule propuso dos transformaciones para los odds ratios, la primera en (Yule 1900),
\[\begin{eqnarray*} \frac{OR-1}{OR+1}, \end{eqnarray*}\] y la segunda en (Yule 1912), \[\begin{eqnarray*} \frac{\sqrt{OR}-1}{\sqrt{OR}+1}. \end{eqnarray*}\]
Si bien estos estadísticos brindan la misma información que los odds ratios originales \(OR\), tienen la ventaja de tomar valores en el intervalo \([-1,1]\), lo que las hace más fáciles de interpretar. En una sección posterior, también veremos que las distribuciones marginales no tienen efecto en la Fr\(\acute{e}\)chet-H\(\ddot{o}\)effding de la correlación tetracórica, otra medida de asociación, ver también, (Joe 2014), página 48.
\[ {\small \begin{matrix} \begin{array}{l|rr|r} \hline & \text{Fire5} & & \\ \text{NoClaimCredit} & 0 & 1 & \text{Total} \\ \hline 0 & 1611 & 2175 & 3786 \\ 1 & 897 & 956 & 1853 \\ \hline \text{Total} & 2508 & 3131 & 5639 \\ \hline \end{array} \end{matrix}} \] Table 14.2 : 2 \(\times\) 2 tabla de frecuencias para las variables Fire5 y NoClaimCredit de la base de datos LGPIF.
A partir de la Table 14.2, \(OR(\pi_{11})=\frac{1611(956)}{897(2175)}=0,79\). Se puede obtener el \(OR(\pi_{11})\), usando la función oddsratio() de la librería epitools de R. Del siguiente resultado, \(OR(\pi_{11})=0,79\) para las variables binarias NoClaimCredit y Fier5 de la base de datos LGPIF.
Código R para Odds Ratios
14.2.3.2 Variables Categóricas
Más generalmente, sea \((X,Y)\) un par bivariante con número de categorías \(ncat_X\) y \(ncat_Y\), respectivamente. Para una tabla de frecuencias de doble entrada, sea \(n_{jk}\) el número en la \(j\)ésima fila, columna \(k\). Sea \(n_{j\centerdot}\) el total de la marginal de la fila, \(n_{\centerdot k}\) el total de la marginal de la columna y \(n=\sum_{j,k} n_{j,k}\). Se define el estadístico chi-cuadrado de Pearson como
\[\begin{eqnarray*} \chi^2 = \sum_{jk} \frac{(n_{jk}- n_{j\centerdot}n_{\centerdot k}/n)^2}{n_{j\centerdot}n_{\centerdot k}/n} . \end{eqnarray*}\]
El estadístico contraste ratio de verosimilitud es
\[\begin{eqnarray*} G^2 = 2 \sum_{jk} n_{jk} \ln\frac{n_{jk}}{n_{j\centerdot}n_{\centerdot k}/n} . \end{eqnarray*}\]
Bajo el supuesto de independencia, tanto \(\chi^2\) como \(G^2\) tienen una distribución asintótica de Chi-cuadrado con \((ncat_X-1)(ncat_Y-1)\) grados de libertad.
Para ayudar a ver lo que estos estadísticos están estimando, sea \(\pi_{jk} = \Pr(X=j, Y=k)\) y sea \(\pi_{X,j}=\Pr(X=j)\) y similar para \(\pi_{Y,k}\). Suponiendo que \(n_{jk}/n \approx \pi_{jk}\) para \(n\) grandes y de manera similar para las probabilidades marginales, tenemos
\[\begin{eqnarray*} \frac{\chi^2}{n} \approx \sum_{jk} \frac{(\pi_{jk}- \pi_{X,j}\pi_{Y,k})^2}{\pi_{X,j}\pi_{Y,k}} \end{eqnarray*}\]
y
\[\begin{eqnarray*} \frac{G^2}{n} \approx 2 \sum_{jk} \pi_{jk} \ln\frac{\pi_{jk}}{\pi_{X,j}\pi_{Y,k}} . \end{eqnarray*}\]
Bajo la hipótesis nula de independencia, tenemos \(\pi_{jk} =\pi_{X,j}\pi_{Y,k}\) y está claro, a partir de las aproximaciones anteriores que anticipamos que estos estadísticos tomarán valores pequeños bajo esta hipótesis.
Los enfoques clásicos, como se describe en (Y. M. Bishop, Fienberg, and Holland 1975) (página 374), distinguen entre pruebas de independencia y medidas de asociación. Los primeros están diseñados para detectar si existe una relación, mientras que los segundos están destinados a evaluar el tipo y el alcance de una relación. Reconocemos estos diferentes propósitos, pero también esta distinción nos preocupa menos en las aplicaciones actuariales.
\[ {\small \begin{matrix} \begin{array}{l|rr} \hline & \text{NoClaimCredit} & \\ \text{EntityType} & 0 & 1 \\ \hline \text{City} & 644 & 149 \\ \text{County} & 310 & 18 \\ \text{Misc} & 336 & 273 \\ \text{School} & 1103 & 494 \\ \text{Town} & 492 & 479 \\ \text{Village} & 901 & 440 \\ \hline \end{array} \end{matrix}} \]
Table 14.3 : Tabla de frecuencias de doble entrada para las variables EntityType y NoClaimCredit a partir de la base de datos LGPIF.
Se puede obtener el estadístico Chi-cuadrado de Pearson utilizando la función chisq.test() de la librería MASS en R. Aquí, probamos si la variable EntityType es independiente de la variable NoClaimCredit usando Table 14.3.
Código R para el Estadístico Chi-cuadrado de Pearson
Como el P valor es inferior al nivel de significación de 0,05, rechazamos la hipótesis nula de que EntityType es independiente de NoClaimCredit.
Además, se puede obtener el estadístico para el contraste de razón de verosimilitud utilizando la función likelihood.test() de la librería Deducer en R. A continuación, probamos si la variable EntityType es independiente de la variable NoClaimCredit, ambas de la base de datos LGPIF. Se llega a la misma conclusión que en el contraste Chi-cuadrado de Pearson.
Código R Code del Estadístico para el Contraste de Razón de Verosimilitud
14.2.4 Variables Ordinales
A medida que el analista pasa de la escala continua a la nominal, existen dos fuentes principales de pérdida de información (Y. M. Bishop, Fienberg, and Holland 1975) (página 343). La primera se debe a que se dividen las mediciones continuas precisas en grupos. La segunda es debida a la pérdida del ordenamiento de los grupos. Entonces, es sensato describir lo que podemos hacer con variables que están en grupos discretos pero donde se conoce el orden.
Como se describe en la Sección 14.1.1, las variables ordinales proporcionan un orden claro de los niveles de una variable, pero se desconocen las distancias entre dichos niveles. Las asociaciones se han cuantificado tradicionalmente de forma paramétrica utilizando correlaciones basadas en la normal y de forma no paramétrica utilizando correlaciones de Spearman con rangos empatados.
14.2.4.1 Enfoque Paramétrico Utilizando Correlaciones Basadas en la Normal
Se hace referencia a la página 60, Sección 2.12.7 de (Joe 2014). Sea \((y_1,y_2)\) un par bivariado con valores discretos en \(m_1, \ldots, m_2\). Para una tabla de doble entrada de frecuencias ordinales, sea \(n_{st}\) el número en la \(s\)ésima fila, columna \(t\). Sea \((n_{m_1\centerdot}, \ldots, n_{m_2\centerdot})\) los totales de las marginales por filas, sea \((n_{\centerdot m_1}, \ldots, n_{\centerdot m_2})\) los totales por columnas y sea \(n=\sum_{s,t} n_{s,t}\) el total de por filas y columnas.
Sea \(\hat{\xi}_{1s} = \Phi^{-1}((n_{m_1}+\cdots+n_{s\centerdot})/n)\) para \(s=m_1, \ldots, m_2\) un punto de corte y de manera similar para \(\hat{\xi}_{2t}\). La correlación policórica, basada en un procedimiento de estimación en dos pasos, es
\[\begin{eqnarray*} \begin{array}{cr} \hat{\rho_N} &=\text{argmax}_{\rho} \sum_{s=m_1}^{m_2} \sum_{t=m_1}^{m_2} n_{st} \log\left\{ \Phi_2(\hat{\xi}_{1s}, \hat{\xi}_{2t};\rho) -\Phi_2(\hat{\xi}_{1,s-1}, \hat{\xi}_{2t};\rho) \right.\\ & \left. -\Phi_2(\hat{\xi}_{1s}, \hat{\xi}_{2,t-1};\rho) +\Phi_2(\hat{\xi}_{1,s-1}, \hat{\xi}_{2,t-1};\rho) \right\} \end{array} \end{eqnarray*}\]
Se llama correlación tetracórica para variables binarias.
\[ {\small \begin{matrix} \begin{array}{l|rr} \hline & \text{NoClaimCredit} & \\ \text{AlarmCredit} & 0 & 1 \\ \hline 1 & 1669 & 942 \\ 2 & 121 & 118 \\ 3 & 195 & 132 \\ 4 & 1801 & 661 \\ \hline \end{array} \end{matrix}} \]
Table 14.4 : Tabla de frecuencias de doble entrada para las variables AlarmCredit y NoClaimCredit de la base de datos LGPIF.
Se puede obtener la correlación policórica o tetracórica usando la función polychoric() o tetrachoric() de la librería psych en R. La correlación policórica se ilustra utilizando Table 14.4. \(\hat{\rho}_N=-0,14\), lo que significa que existe una relación negativa entre AlarmCredit y NoClaimCredit.
Código R para la Correlación Policórica
14.2.5 Variables de Intervalo
Como se describe en la Sección 14.1.2, las variables de intervalo proporcionan una ordenación clara de los niveles de una variable y la distancia numérica entre dos niveles cualquiera de la escala se puede interpretar fácilmente. Por ejemplo, la variable del grupo de edad de los conductores es una variable de intervalo.
Para medir la asociación, tienen sentido tanto el enfoque de variable continua como el de variable ordinal. El primero aprovecha el conocimiento del ordenamiento aunque supone continuidad. El último no se basa en la continuidad y tampoco hace uso de la información dada por la distancia entre escalas.
14.2.6 Variables discretas y continuas
La correlación poliserial se define de manera similar, cuando una variable (\(y_1\)) es continua y la otra (\(y_2\)) ordinal. Se define \(z\) para que sea el normal score de \(y_1\). La correlación poliserial es
\[\begin{eqnarray*} \hat{\rho_N} = \text{argmax}_{\rho} \sum_{i=1}^n \log\left\{ \phi(z_{i1})\left[ \Phi(\frac{\hat{\xi}_{2,y_{i2}} - \rho z_{i1}} {(1-\rho^2)^{1/2}}) -\Phi(\frac{\hat{\xi}_{2,y_{i2-1}} - \rho z_{i1}} {(1-\rho^2)^{1/2}}) \right] \right\} \end{eqnarray*}\]
La correlación biserial se define de manera similar, cuando una variable es continua y la otra binaria.
\[ {\small \begin{matrix} \begin{array}{l|r|r} \hline \text{NoClaimCredit} & \text{Mean} &\text{Total} \\ & \text{Claim} &\text{Claim} \\ \hline 0 & 22.505 & 85.200.483 \\ 1 & 6.629 & 12.282.618 \\ \hline \end{array} \end{matrix}} \]
Table 14.5 : Resumen de la variable Claim para las categorías de NoClaimCredit de la base de datos LGPIF.
Se puede obtener la correlación poliserial o biserial usando la función polyserial() o biserial() de la librería psych en R. Table 14.5 da el resumen de Claim por NoClaimCredit y la correlación biserial se ilustra a continuación usando el código ‘R.’ El \(\hat{\rho}_N=-0,04\) significa que hay una correlación negativa entre Claim y NoClaimCredit.
Código R para la Correlación Biserial
14.3 Introducción a Copulas
Las funciones de cópula se utilizan ampliamente en la literatura relacionada con la estadística y la ciencia actuarial para el modelado de dependencia.
En esta sección aprenderemos como:
- Describir una función de distribución multivariante en términos de función de cópula.
Una copula es una función de distribución multivariada con marginales uniformes. Específicamente, sean \(U_1, \ldots, U_p\) \(p\) variables aleatorias uniformes en \((0,1)\). Su función de distribución \[{C}(u_1, \ldots, u_p) = \Pr(U_1 \leq u_1, \ldots, U_p \leq u_p),\] es una cópula. Buscamos usar cópulas en aplicaciones que se basan en algo más que datos distribuidos uniformemente. Por lo tanto, considere funciones de distribución marginales arbitrarias \({F}_1(y_1)\),…,\({F}_p(y_p)\). Entonces, podemos definir una función de distribución multivariante usando la cópula tal que \[{F}(y_1, \ldots, y_p)= {C}({F}_1(y_1), \ldots,{F}_p(y_p) ).\]
Aquí, \(F\) es una función de distribución multivariante en esta ecuación. Sklar (1959) demostró que \(cualquier\) función de distribución multivariante \(F\), puede escribirse en la forma de esta ecuación, es decir, usando una representación de cópula.
Sklar también mostró que, si las distribuciones marginales son continuas, entonces hay una representación de cópula única. En este capítulo nos centramos en el modelado de cópulas con variables continuas. Para casos discretos, los lectores pueden ver (Joe 2014) y (Genest and Nešlohva 2007).
Para el caso bivariante, \(p=2\), la función de distribución de dos variables aleatorias puede escribirse mediante la función de cópula bivariante:
\[{C}(u_1, \, u_2) = \Pr(U_1 \leq u_1, \, U_2 \leq u_2),\]
\[{F}(y_1, \, y_2)= {C}({F}_1(y_1), \, {F}_p(y_2)).\]
Para dar un ejemplo de cópula bivariante, podemos analizar la cópula de Frank (1979). La ecuación es \[{C}(u_1,u_2) = \frac{1}{\theta} \ln \left( 1+ \frac{ (\exp(\theta u_1) -1)(\exp(\theta u_2) -1)} {\exp(\theta) -1} \right).\]
Esta es una función de distribución bivariante con su dominio en el cuadrado unitario \([0,1]^2.\) Aquí \(\theta\) es el parámetro de dependencia y el rango de dependencia está controlado por este parámetro \(\theta\). La asociación positiva aumenta a medida que aumenta \(\theta\) y esta asociación positiva se puede resumir con rho de Spearman (\(\rho\)) y tau de Kendall (\(\tau\)). La cópula de Frank es una de las funciones de cópula de uso común en la literatura de cópula. Veremos otras funciones de cópula en la Sección 14.5.
14.4 Aplicación usando Cópulas
En esta sección aprenderemos como:
- Descubrir la estructura de dependencia entre las variables aleatorias
- Modelizar la dependencia con cópulas
Esta sección analiza los datos de losses (pérdidas) y expenses (gastos) de seguros con el programa estadístico R. Este conjunto de datos se introdujo en (Edward W. Frees and Valdez 1998) y ahora está disponible en el paquete copula. El proceso de ajuste del modelo se inicia con el modelado marginal de dos variables (losses y expenses).
Posteriormente modelizamos la distribución conjunta de estos resultados marginales.
14.4.1 Descripción de los Datos
Comenzamos obteniendo una muestra (\(n = 1500\)) de todos los datos. Consideramos las dos primeras variables de los datos; losses y expenses.
- losses: reclamaciones de responsabilidad general de Insurance Services Office, Inc. (ISO)
- expenses: ALAE, específicamente atribuibles a la liquidación de reclamaciones individuales (por ejemplo, honorarios de abogados, gastos de investigación de reclamaciones)
Para visualizar la relación entre losses y expenses (ALAE), se crean diagramas de dispersión en la figura 14.2 en la escala real en dólares y en la escala logarítmica.
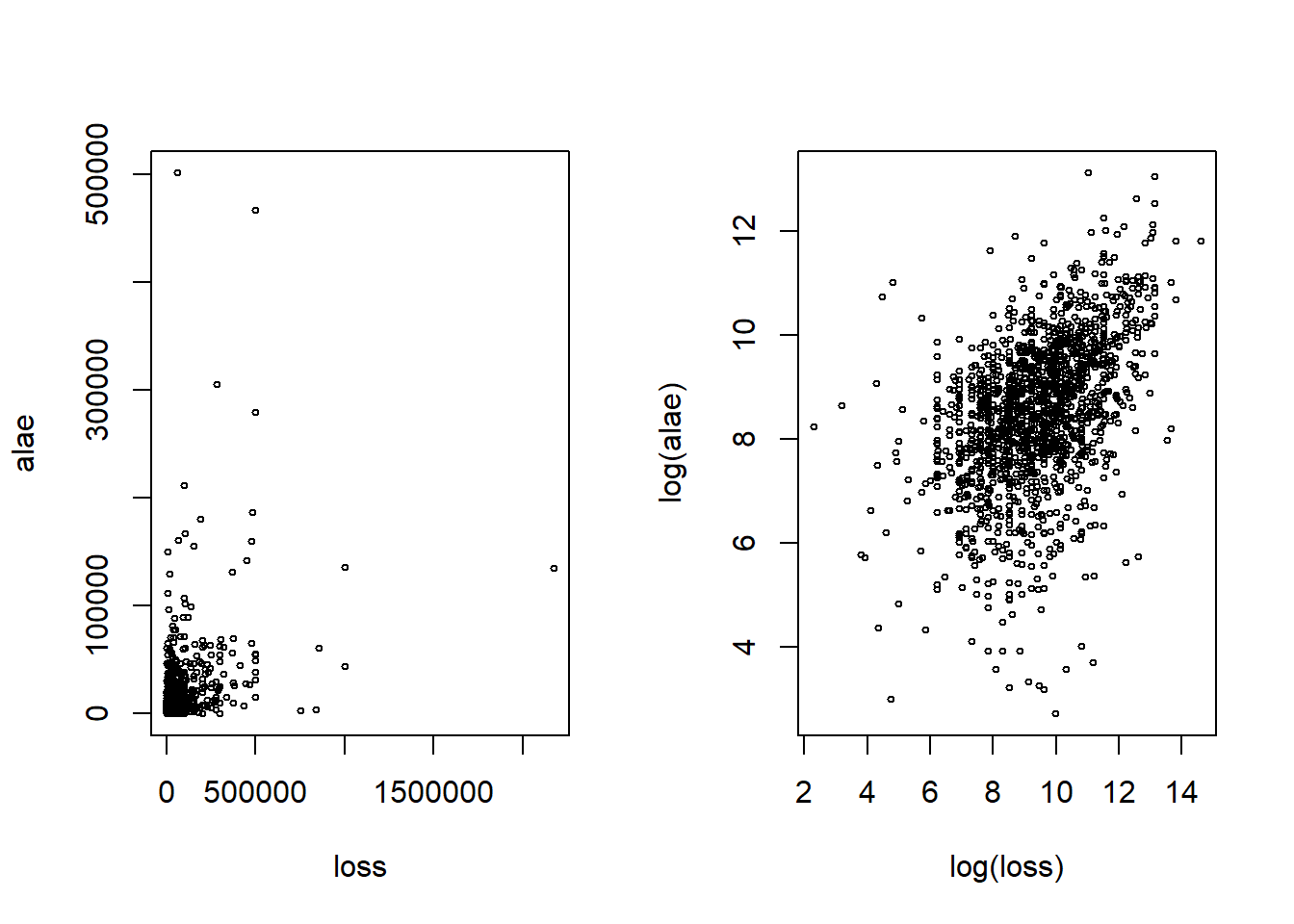
Figure 14.2: Scatter plot of Loss and ALAE
Código R para gráfico de dispersión
14.4.2 Modelos Marginales
Primero examinamos las distribuciones marginales de losses y expenses antes de pasar por el modelo conjunto. Los histogramas muestran que tanto las losses como los expenses son variables asimétricas a la derecha y con cola pesada.
Para distribuciones marginales de pérdidas y gastos, consideramos una distribución de tipo Pareto, es decir, una distribución de tipo II de Pareto con función de distribución \[ F(y)=1- \left( 1 + \frac{y}{\theta} \right) ^{-\alpha},\] donde \(\theta\) es el parámetro de escala y \(\alpha\) es el parámetro de forma.
Las distribuciones marginales de pérdidas y gastos se ajustan con máxima verosimilitud. Específicamente, usamos la función \(vglm\) del paquete R VGAM. En primer lugar, ajustamos la distribución marginal de gastos.
Código R para el Ajuste de la Pareto
Repetimos este procedimiento para ajustar la distribución marginal de la variable losses. Debido a que los datos de pérdida también parecen datos asimétricos a la derecha y de cola pesada, también modelizamos la distribución marginal con la distribución de Pareto II.
Código R para el Ajuste de la Pareto
Para visualizar la distribución ajustada de las variables losses y expenses, utilizamos los parámetros estimados y trazamos la función de distribución y de la función de densidad correspondientes. Para obtener más detalles sobre la selección del modelo marginal, consulte el Capítulo 4.
###Transformación Integral de Probabilidad
La transformación integral de probabilidad muestra que cualquier variable continua se puede mapear como una variable aleatoria \(U(0,1)\) a través de su función de distribución.
Dada la distribución Pareto II ajustada, la variable expenses se transforma en la variable \(u_1\), que sigue una distribución uniforme en \([0,1]\):
\[u_1 = 1 - \left( 1 + \frac{ALAE}{\hat{\theta}} \right)^{-\hat{\alpha}}.\]
Después de aplicar la transformación integral de probabilidad a la variable expenses, trazamos el histograma de ALAE Transformada en la Figura 14.3.
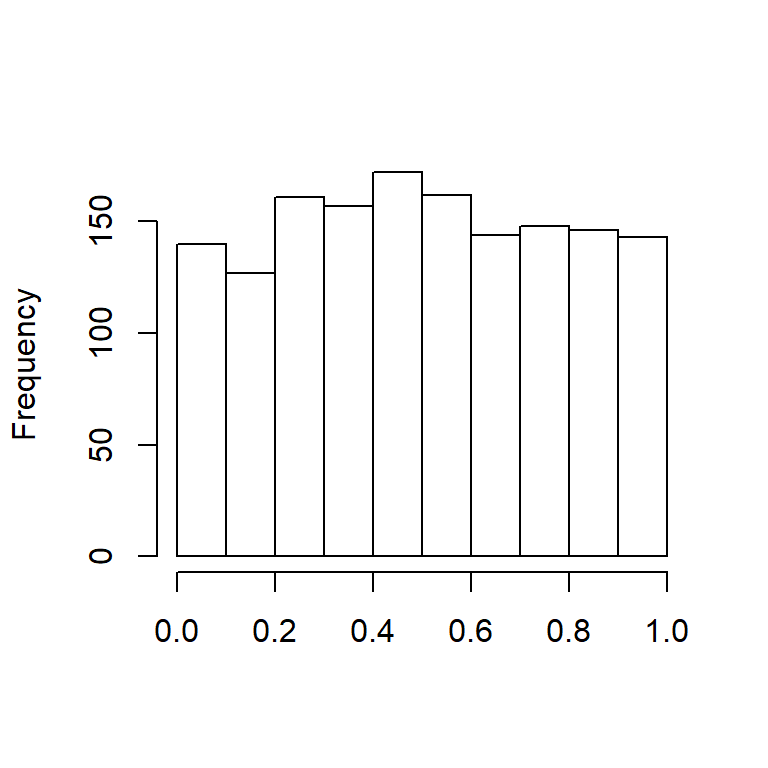
Figure 14.3: Histograma de ALAE transformada
Después del proceso de ajuste, la variable loss también se transforma en la variable \(u_2\), que sigue una distribución uniforme en \([0,1]\). Trazamos el histograma de Loss transformada . Como alternativa, la variable loss se transforma en \(normal\) \(scores\) con la función cuantil de la distribución normal estándar. Como vemos en la Figura 14.4, las puntuaciones normales de la variable loss son aproximadamente marginalmente normal estándar.
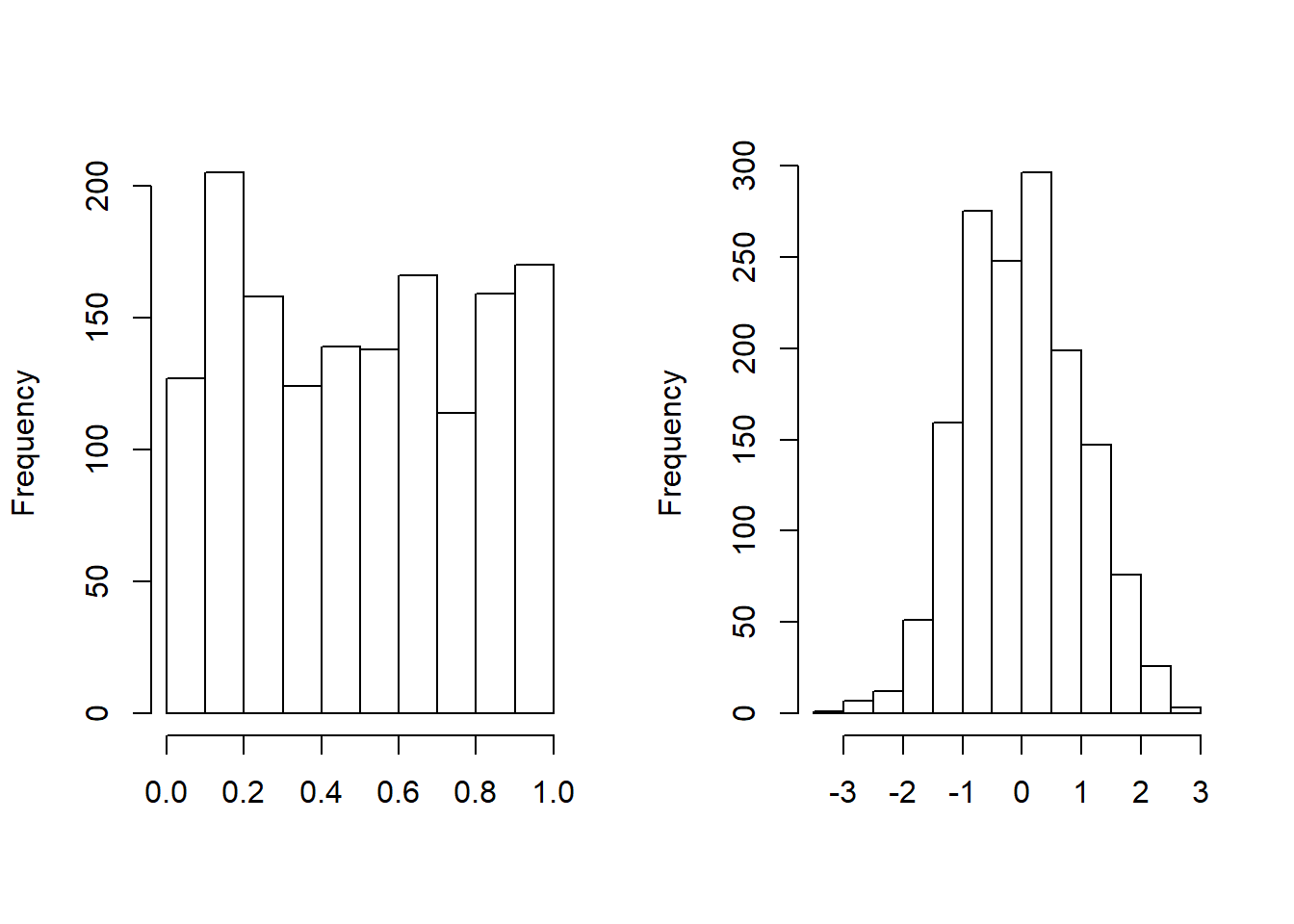
Figure 14.4: Histograma de la Pérdida Transformada. El gráfico de la izquierda muestra la distribución de pérdidas transformadas integrales de probabilidad. El gráfico de la derecha muestra la distribución de las puntuaciones normales correspondientes.
Código R de las Variables Transformadas
14.4.3 Modelización Conjunta con Función de Cópula
Antes de modelizar conjuntamente las pérdidas y los gastos, dibujamos el diagrama de dispersión de las variables transformadas \((u_1, u_2)\) y el diagrama de dispersión de las puntuaciones normales en la figura 14.5.
Posteriormente, calculamos la rho de Spearman entre estas dos variables aleatorias uniformes.
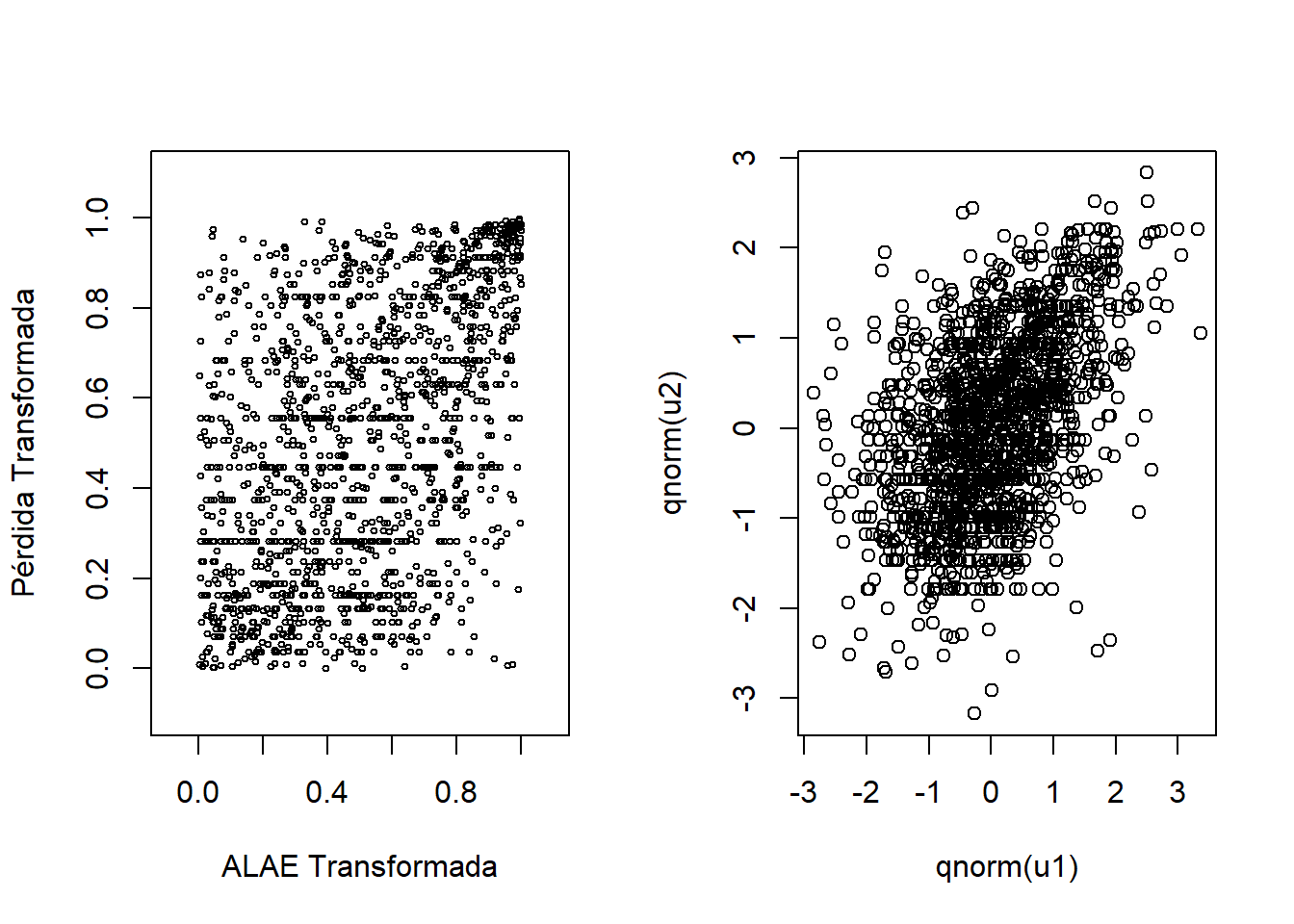
Figure 14.5: Izquierda: Gráfico de Dispersión para variables transformadas. Derecha: Gráfico de Dispersión para puntuaciones normales
Código R para el Gráfico de Dispersión y la Correlación
Los gráficos de dispersión y el valor de correlación rho de Spearman (0,451) nos muestran que existe una dependencia positiva entre estas dos variables aleatorias uniformes. Es más claro ver la relación con las puntuaciones normales en el segundo gráfico. Para conocer más detalles sobre las puntuaciones normales y sus aplicaciones en el modelado de cópulas, consulte (Joe 2014).
\((U_1, U_2)\), (\(U_1 = F_1(ALAE)\) y \(U_2=F_2(LOSS)\)), se ajusta a la cópula de Frank con el método de máxima verosimilitud.
Código R para la modelización con Cópula de Frank
El modelo ajustado implica que las pérdidas y los gastos son positivamente dependientes y su dependencia es significativa.
Usamos el parámetro ajustado para actualizar la cópula de Frank. La correlación de Spearman correspondiente al parámetro de cópula ajustado (3.114) se calcula con la función rho. En este caso, el coeficiente de correlación de Spearman es 0,462, que está muy cerca del coeficiente de correlación de Spearman de la muestra; 0,452.
R Code for Spearman’s Correlation Using Frank’s Copula
Para visualizar la cópula de Frank ajustada, las gráficas de perspectiva de la función de distribución y la función de densidad se dibujan en la Figura 14.6.
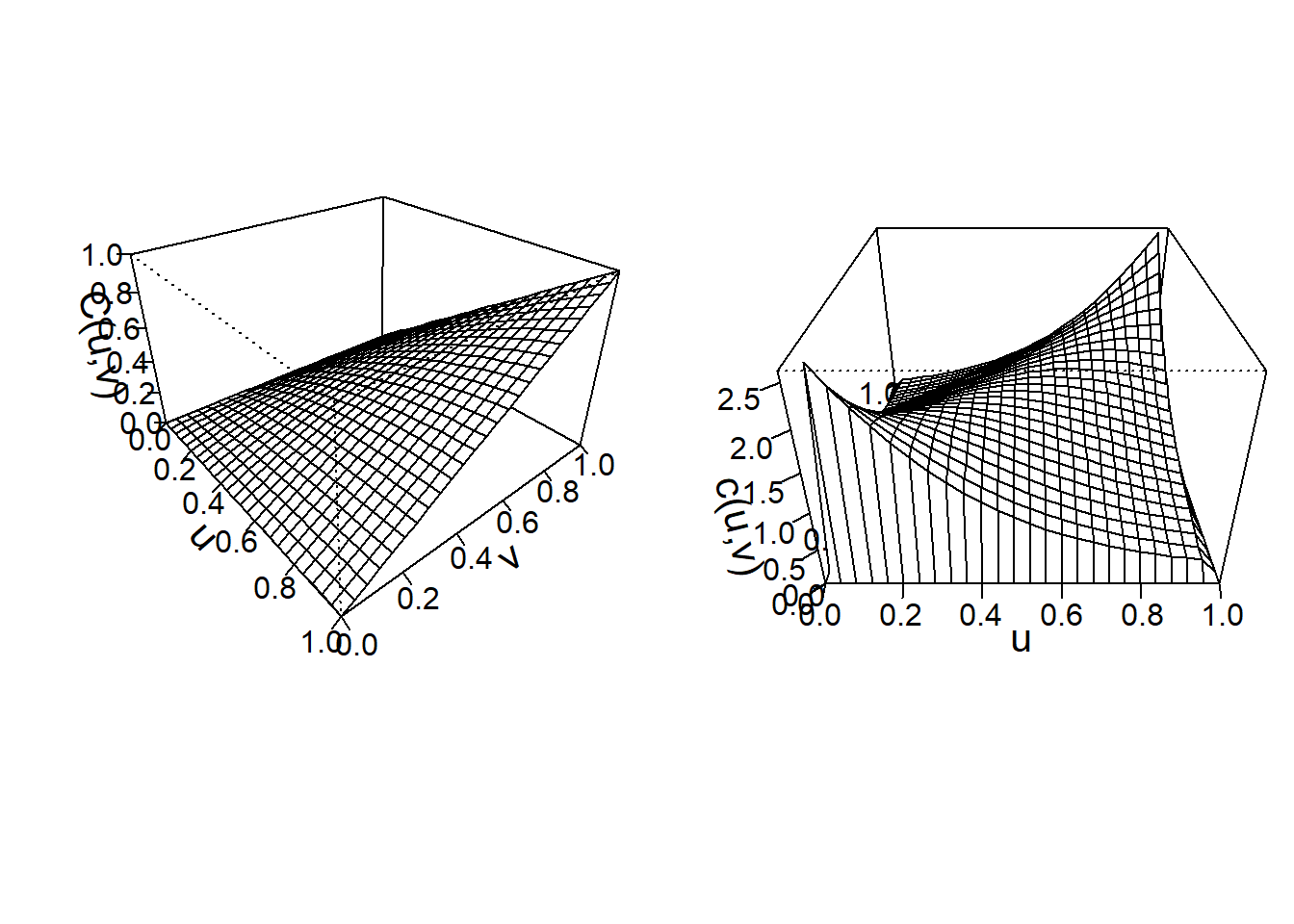
Figure 14.6: Izquierda: Gráfico de función de distribución para Franks Copula. Derecha: Gráfico de la función de densidad para Franks Copula
Código R para el gráfico de la Cópula de Frank
La cópula de Frank modeliza la dependencia positiva para este conjunto de datos, con \(\theta=3,114\). Para la cópula de Frank, la dependencia está relacionada con los valores de \(\theta\). Es decir: * \(\theta=0\): copula de independencia * \(\theta>0\): dependencia positiva * \(\theta<0\): dependencia negativa
14.5 Tipos de Cópulas
En esta sección aprenderemos como:
- Definir las familias básicas de las funciones de cópula
- Calcular los coeficientes de asociación con la ayuda de las funciones de cópula.
Hay varias familias de cópulas que se han descrito en la literatura. Dos familias principales entre todas ellas son las cópulas Arquimedianas y las Elípticas.
14.5.1 Cópulas Elípticas
Cópulas elípticas se construyen a partir de distribuciones elípticas. Esta cópula descompone las distribuciones elípticas (multivariantes) en sus distribuciones marginales elípticas univariantes según el teorema de Sklar (Hofert et al. 2018).
Las propiedades de las cópulas elípticas normalmente se obtienen a partir de las propiedades de las distribuciones elípticas correspondientes (Hofert et al. 2018).
Por ejemplo, la distribución normal es un tipo especial de distribución elíptica. Para introducir la clase elíptica de cópulas, comenzamos con la conocida distribución normal multivariante con función de densidad de probabilidad \[\phi_N (\mathbf{z})= \frac{1}{(2 \pi)^{p/2}\sqrt{\det \boldsymbol \Sigma}} \exp\left( -\frac{1}{2} \mathbf{z}^{\prime} \boldsymbol \Sigma^{-1}\mathbf{z}\right).\]
Aquí, \(\boldsymbol \Sigma\) es una matriz de correlación, con unos en la diagonal. Supongamos que \(\Phi\) y \(\phi\) denotan las funciones de distribución y de densidad de la normal estándar. Definimos la función de densidad de cópula gaussiana (normal) como
\[{c}_N(u_1, \ldots, u_p) = \phi_N \left(\Phi^{-1}(u_1), \ldots, \Phi^{-1}(u_p) \right) \prod_{ j=1}^p \frac{1}{\phi(\Phi^{-1}(u_j))}.\]
Como en otras cópulas, el dominio es el cubo unitario \([0,1]^p\).
Específicamente, un vector \(p\)-dimensional \({z}\) tiene una \({distribución}\) \({elíptica}\) si la densidad se puede escribir como \[h_E (\mathbf{z})= \frac{k_p}{\sqrt{\det \boldsymbol \Sigma}} g_p \left( \frac{1}{2} (\mathbf{z}- \boldsymbol \mu)^{\prime} \boldsymbol \Sigma^{-1}(\mathbf{z}- \boldsymbol \mu) \right).\]
Usaremos distribuciones elípticas para generar cópulas. Debido a que las cópulas se ocupan principalmente de las relaciones, podemos restringir nuestras consideraciones al caso donde \(\mu = \mathbf{0}\) y \(\boldsymbol \Sigma\) es una matriz de correlación. Con estas restricciones, las distribuciones marginales de la cópula elíptica multivariante son idénticas; usamos \(H\) para referirnos a esta función de distribución marginal y \(h\) es la densidad correspondiente. Esta densidad marginal es \(h(z) = k_1 g_1(z^2/2).\)
Ahora estamos listos para definir la \(cópula\) \(elíptica\), una función definida en el cubo unitario \([0,1]^p\) como
\[{c}_E(u_1, \ldots, u_p) = h_E \left(H^{-1}(u_1), \ldots, H^{-1}(u_p) \right) \prod_{j=1}^p \frac{1}{h(H^{-1}(u_j))}.\]
En la familia de las cópulas elípticas, la función \(g_p\) se conoce como generador porque puede utilizarse para generar distribuciones alternativas.
\[ \small\begin{array}{lc} \hline & Generador \\ Distribución & \mathrm{g}_p(x) \\ \hline \text{Distribución Normal } & e^{-x}\\ \text{Distribución t con r grados de libertad} & (1+2x/r)^{-(p+r)/2}\\ \text{Cauchy} & (1+2x)^{-(p+1)/2}\\ \text{Logística} & e^{-x}/(1+e^{-x})^2\\ \text{Potencia Exponencial } & \exp(-rx^s)\\ \hline \end{array} \]
Table 14.6 : Funciones generadoras y de distribución (\(\mathrm{g}_p(x)\)) para las cópulas elípticas seleccionadas
La mayor parte del trabajo empírico se centra en la cópula normal y la cópula \(t\). Es decir, las cópulas \(t\) son útiles para modelizar la dependencia en las colas de distribuciones bivariadas, especialmente en aplicaciones de análisis de riesgos financieros.
Las \(t\)-cópulas con el mismo parámetro de asociación, al variar el parámetro de grados de libertad nos muestran diferentes estructuras de dependencia de cola. Para obtener más información sobre las cópulas \(t\), los lectores pueden consultar (Joe 2014), (Hofert et al. 2018).
14.5.2 Cópulas Arquimedianas
Esta clase de cópulas se construye a partir de una función \(generadora\) \(\mathrm{g}(\cdot)\), que es una función convexa y decreciente con dominio [0,1] y rango \([0, \infty)\) tal que \(\mathrm{g}(0)=0\). Usa \(\mathrm{g}^{-1}\) para la función inversa de \(\mathrm{g}\). Entonces la función
\[\mathrm{C}_{\mathrm{g}}(u_1, \ldots, u_p) = \mathrm{g}^{-1} \left(\mathrm{g}(u_1)+ \cdots + \mathrm{g}(u_p) \right)\]
se dice que es una cópula Arquimediana. La función \(\mathrm{g}\) es conocida como el generador de la cópula \(\mathrm{C}_{\mathrm{g}}\).
Para el caso bivariante, \(p=2\) , la función de cópula Arquimediana puede ser escrita por la función
\[\mathrm{C}_{\mathrm{g}}(u_1, \, u_2) = \mathrm{g}^{-1} \left(\mathrm{g}(u_1) + \mathrm{g}(u_2) \right).\]
Algunos casos especiales importantes de cópulas Arquimedianas son la cópula de Frank, la cópula de Clayton/Cook-Johnson y la cópula de Gumbel/Hougaard. Estas clases de cópula se derivan de diferentes funciones generadoras.
Recuerde que describimos detalladamente la cópula de Frank en la Sección 14.3 y en la Sección 14.4. Aquí continuaremos expresando las ecuaciones para la cópula de Clayton y la cópula de Gumbel/Hougaard.
14.5.2.1 Cópula de Clayton
Para \(p=2\), la cópula Clayton está parametrizada por \(\theta \in [-1,\infty)\) y está definida por \[C_{\theta}^C(u)=\max\{u_1^{-\theta}+u_2^{-\theta}-1,0\}^{1/\theta}, \quad u\in[0,1]^2.\]
Esta es una función de distribución bivariante de la cópula de Clayton definida en el cuadrado unitario \([0,1]^2.\) El rango de dependencia está controlado por el parámetro \(\theta\) al igual que la cópula de Frank.
14.5.2.2 Cópula de Gumbel-Hougaard
La cópula de Gumbel-Hougaarg está parametrizada por \(\theta \in [1,\infty)\) y definida por \[C_{\theta}^{GH}(u)=\exp\left(-\left(\sum_{i=1}^2 (-\log u_i)^{\theta}\right)^{1/\theta}\right), \quad u\in[0,1]^2.\]
Los lectores que busquen antecedentes más detallados sobre las cópulas Arquímedianas pueden consultar Joe (2014), Edward W. Frees and Valdez (1998) y Genest and Mackay (1986).
14.5.3 Propiedades de las Cópulas
14.5.3.1 Cotas y Asociación
Como todas las funciones de distribución multivariante, las cópulas están acotadas. Los límites de Fr\('{e}\)chet-Hoeffding son
\[\max( u_1 +\cdots+ u_p + p -1, 0) \leq \mathrm{C}(u_1, \ldots, u_p) \leq \min (u_1, \ldots,u_p).\]
Para deducir el lado derecho de la ecuación, tenga en cuenta que \(\mathrm{C}(u_1,\ldots, u_p) = \Pr(U_1 \leq u_1, \ldots, U_p \leq u_p) \leq \Pr(U_j \leq u_j)\), para \(j=1,\ldots,p\). El límite se logra cuando \(U_1 = \cdots = U_p\). Para el lado izquierdo cuando \(p=2\), considere \(U_2=1-U_1\). En este caso, si \(1-u_2 < u_1\) entonces \(\Pr(U_1 \leq u_1, U_2 \leq u_2) = \Pr ( 1-u_2 \leq U_1 < u_1) =u_1+u_2-1.\) (nelsen1997introducción? )
La cópula producto \(\mathrm{C}(u_1,u_2)=u_1u_2\) es el resultado de asumir independencia entre variables aleatorias.
El límite inferior se logra cuando las dos variables aleatorias están perfectamente relacionadas negativamente (\(U_2=1-U_1\)) y el límite superior se logra cuando están perfectamente relacionado positivamente (\(U_2=U_1\)).
En la Figura 14.7 podemos ver el Frechet-Hoeffdingbounds para dos variables aleatorias.
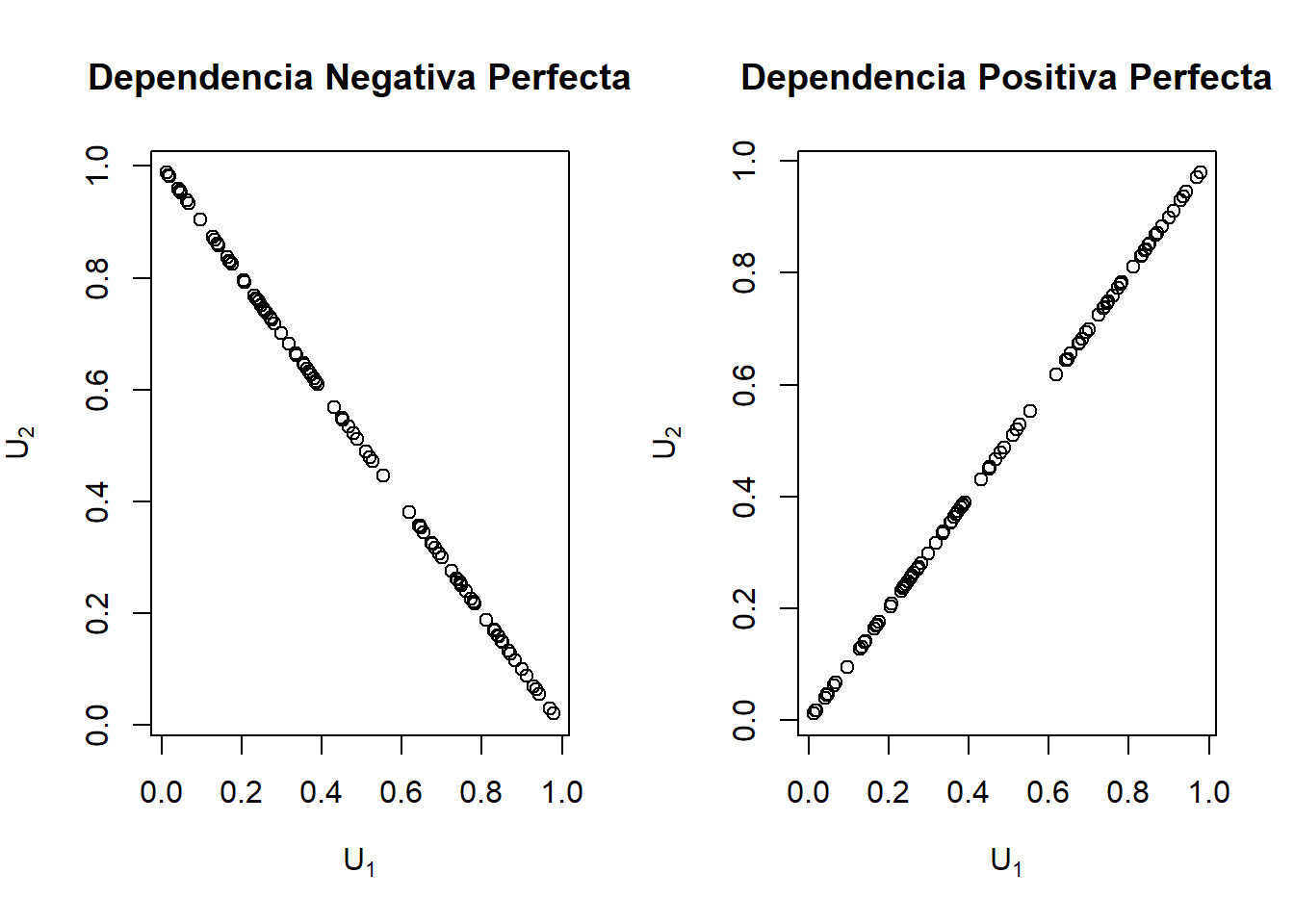
Figure 14.7: Gráficas de dependencia Perfecta Positiva y Negativa
Código R para las Cotas de Frechet-Hoeffding para dos Variables Aleatorias
14.5.3.2 Medidas de Asociación
Schweizer y Wolff (1981) establecieron que la cópula explica toda la dependencia entre dos variables aleatorias, \(Y_1\) y \(Y_2\), en el siguiente sentido. Considere m\(_1\) y m\(_2\) funciones estrictamente crecientes. Por lo tanto, la forma en que \(Y_1\) y \(Y_2\) “se mueven juntas” es capturada por la cópula, independientemente de la escala en la que se mida cada variable.
Schweizer y Wolff también demostraron que las dos medidas estándar de asociación no paramétricas pueden expresarse únicamente en términos de la función de cópula. El coeficiente de correlación de Spearman viene dado por
\[= 12 \int \int \left\{\mathrm{C}(u,v) - uv \right\} du dv.\]
La tau de Kendall viene dada por:
\[= 4 \int \int \mathrm{C}(u,v)d\mathrm{C}(u,v) - 1 .\]
Para estas expresiones, asumimos que \(Y_1\) y \(Y_2\) tienen una función de distribución continua conjunta. Además, la definición de la tau de Kendall usa una copia independiente de (\(Y_1\), \(Y_2\)), etiquetada (\(Y_1^{\ast}\), \(Y_2^{\ast}\)), para definir la medida de “concordancia.” La correlación de Pearson ampliamente utilizada depende tanto de las marginales como de la cópula y se ve afectada por cambios de escala no lineales.
14.5.3.3 Dependencia de la cola
Hay algunas aplicaciones en las que es útil distinguir la parte de la distribución en la que la asociación es más fuerte. Por ejemplo, en seguros es útil comprender la asociación entre las mayores pérdidas, es decir, la asociación en las colas derechas de los datos.
Para capturar este tipo de dependencia, usamos la función de concentración de cola derecha. Esta función es
\[R(z) = \frac{\Pr(U_1 >z, U_2 > z)}{1-z} =\Pr(U_1 > z | U_2 > z) =\frac{1 - 2z + \mathrm{C}(z,z)}{1-z} .\]
A partir de esta ecuación, \(R(z)\) será igual a \(z\) bajo el supuesto de independencia. Joe (1997) usa el término “parámetro de dependencia de la cola superior” para \(R = \lim_{z \rightarrow 1} R(z)\). De manera similar, la función de concentración de cola izquierda es
\[L(z) = \frac{\Pr(U_1 \leq z, U_2 \leq z)}{z}=\Pr(U_1 \leq z | U_2 \leq z) =\frac{ \mathrm{C}(z,z)}{1-z}.\]
La función de concentración Dependencia de la cola captura la probabilidad de que dos variables aleatorias alcancen valores extremos.
Calculamos las funciones de concentración de cola izquierda y derecha para cuatro tipos diferentes de cópulas; Normal, Frank, Gumbel y t-copula. Después de obtener las funciones de concentración de la cola para cada cópula, mostramos los valores de la función de concentración para estas cuatro cópulas en la Table 14.7. Como en Gary G. Venter (2002), mostramos \(L(z)\) para \(z\leq 0,5\) y \(R(z)\) para \(z>0,5\) en el gráfico de dependencia de cola en la Figura 14.8. Interpretamos el gráfico de dependencia de la cola, en el sentido de que tanto la cópula Frank como la Normal no exhiben dependencia de la cola, mientras que \(t\) y Gumbel pueden hacerlo. La cópula \(t\) es simétrica en su tratamiento de las colas superior e inferior.
\[ {\small \begin{matrix} \begin{array}{l|rr} \hline \text{Cópula} & \text{Inferior} & \text{Superior} \\ \hline \text{Frank} & 0 & 0 \\ \text{Gumbel} & 0 & 0,74 \\ \text{Normal} & 0 & 0 \\ \text{t} & 0,10 & 0,10 \\ \hline \end{array} \end{matrix}} \]
Table 14.7 : Valores de la función de concentración de cola para diferentes cópulas
Código R para las Funciones de Dependencia de la Cola para las Diferentes Cópulas
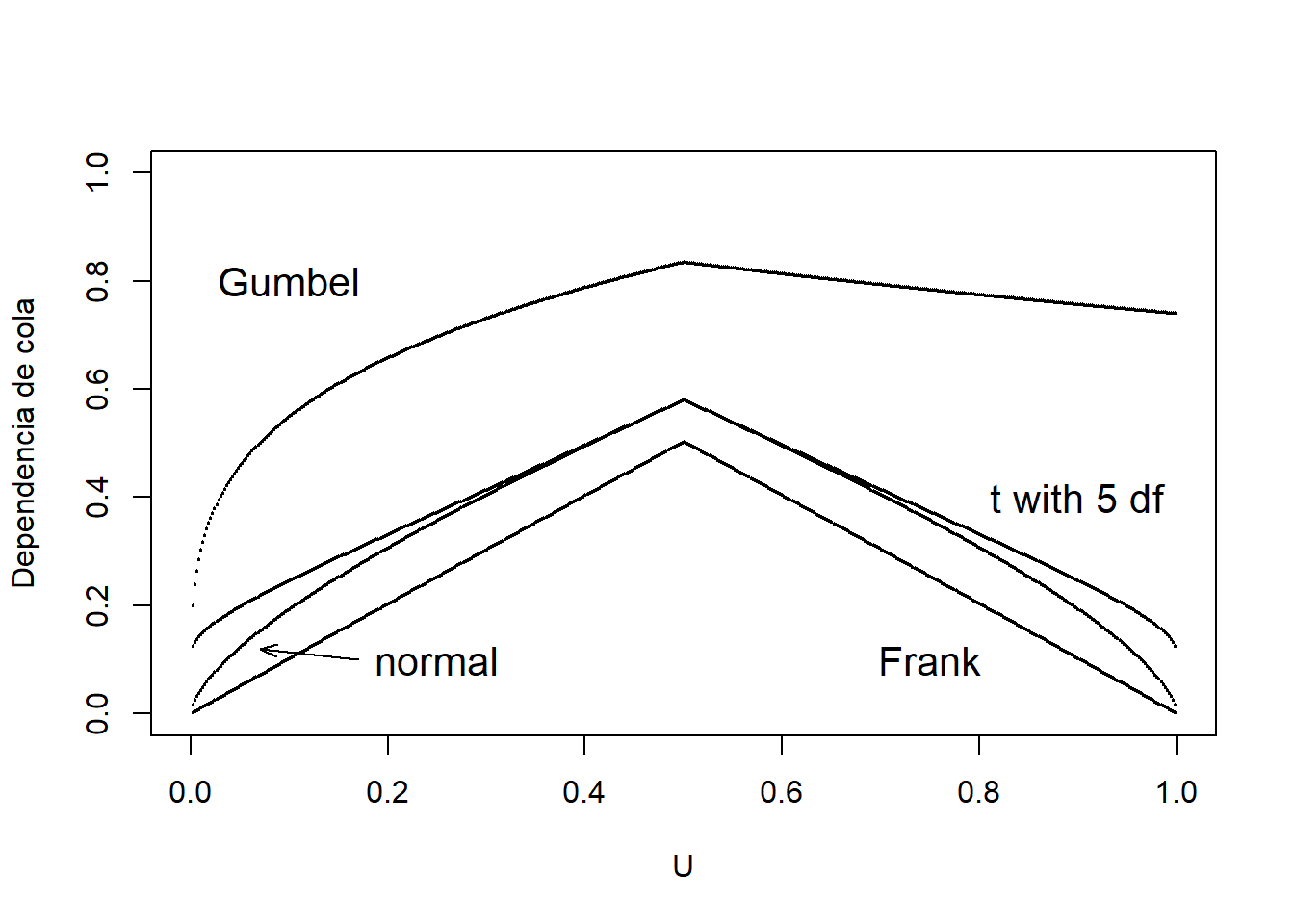
Figure 14.8: Gráficos de dependencia de la cola
Código R para los Gráficos de Dependencia de la Cola para las Diferentes Cópulas
14.6 ¿Por qué es importante la modelización de la dependencia?
La modelización de la dependencia es importante porque nos permite comprender la estructura de dependencia que define la relación entre las variables en un conjunto de datos. En seguros, ignorar el modelo de dependencia puede no afectar la fijación de precios, pero podría conducir a una estimación errónea del capital requerido para cubrir las pérdidas. Por ejemplo, de la Sección 14.4, se ve que hubo una relación positiva entre Pérdida y Gasto. Esto significa que, si hay una gran pérdida, entonces esperamos que los gastos también sean grandes e ignorar esta relación podría conducir a una estimación errónea de las reservas.
Para ilustrar la importancia del modelo de dependencia, le remitimos al ejemplo de Gestión de cartera en el Capítulo 6 que asumió que los riesgos de propiedad y responsabilidad son independientes. Aquí, incorporamos la dependencia al permitir que las 4 líneas de negocio dependan entre sí a través de una cópula gaussiana. En la Table 14.8 mostramos que la dependencia afecta a los cuantiles de la cartera (\(VaR_q\)), aunque no el valor esperado. Por ejemplo, el \(VaR_{0,99}\) de riesgo total que es la cantidad de capital necesaria para asegurar, con un \(99\%\) grado de certeza de que la empresa no se convierta en insolvente técnicamente, es mayor cuando incorporamos la dependencia. Esto lleva a que se asigne menos capital cuando se ignora la dependencia y puede causar problemas inesperados de solvencia.
\[ {\small \begin{matrix} \begin{array}{l|rrrr} \hline \text{Independencia} &\text{Esperado} & VaR_{0,9} & VaR_{0,95} & VaR_{0,99} \\ &\text{Valor} & & & \\ \hline \text{Retenido} & 269 & 300 & 300 & 300 \\ \text{Asegurado} & 2.274 & 4.400 & 6.173 & 11.859 \\ \text{Total} & 2.543 & 4.675 & 6.464 & 12.159 \\ \hline \text{Cópula Gaussiana}&\text{Esperado}& VaR_{0,9} & VaR_{0,95} & VaR_{0,99} \\ &\text{Valor} & & & \\ \hline \text{Retenido} & 269 & 300 & 300 & 300 \\ \text{Asegurado} & 2.340 & 4.988 & 7.339 & 14.905 \\ \text{Total} & 2.609 & 5.288 & 7.639 & 15.205 \\ \hline \end{array} \end{matrix}} \]
Table 14.8 : Resultados para el valor esperado de la cartera y los cuantiles (\(VaR_q\))
Código R para la Simulación Usando la Cópula Gaussiana
14.7 Más Recursos y Contribuciones
Contribuciones
Edward W. (Jed) Frees y Nii-Armah Okine, University of Wisconsin-Madison, y Emine Selin Sarıdaş, Mimar Sinan University, son las principales autores de la versión inicial de este capítulo. Email: jfrees@bus.wisc.edu para comentarios y sugerir mejoras sobre este capítulo.
Traducción al español: Catalina Bolancé (Universitat de Barcelona)
TS 14.A. Otras Medidas Clásicas de Asociaciones Escalares
TS 14.A.1. Blomqvist’s Beta
Blomqvist (1950) desarrolló una medida de dependencia ahora conocida como Blomqvist’s beta, también llamada coeficiente de concordancia media y coeficiente de correlación medial. Usando funciones de distribución, este parámetro se puede expresar como
\[\begin{equation*} \beta = 4F\left(F^{-1}_X(1/2),F^{-1}_Y(1/2) \right) - 1. \end{equation*}\]
Es decir, primero se evalúa cada marginal en su mediana (\(F^{-1}_X(1/2)\) y \(F^{-1}_Y(1/2)\), respectivamente). Luego, se evalúa la función de distribución bivariante en las dos medianas. Después de reescalar (multiplicar por 4 y restar 1), el coeficiente resulta tener un rango de \([-1,1]\), donde 0 es el valor bajo el supuesto de independencia. Al igual que la rho de Spearman y la tau de Kendall, es fácil proporcionar un estimador basado en rangos. Primero se expresa \(\beta = 4C(1/2,1/2)-1 = 2\Pr((U_1-1/2)(U_2-1/2))-1\), donde \(U_1, U_2\) son variables aleatorias uniformes. Luego, se define
\[\begin{equation*} \hat{\beta} = \frac{2}{n} \sum_{i=1}^n I\left( (R(X_{i})-\frac{n+1}{2})(R (Y_{i})-\frac{n+1}{2}) \ge 0 \right)-1 . \end{equation*}\]
Consulte, por ejemplo, (Joe 2014), página 57 o (Hougaard 2000), página 135, para obtener más detalles.
Debido a que el parámetro de Blomqvist se basa en el centro de la distribución, es particularmente útil cuando se censuran los datos; en este caso, la información en las partes extremas de la distribución no siempre es fiable. ¿Cómo afecta esto a la elección de las medidas de asociación? Primero, recuerde que las medidas de asociación se basan en una función de distribución bivariante. Entonces, si uno tiene conocimiento de una buena aproximación de la función de distribución, en principio el cálculo de una medida de asociación es sencillo. En segundo lugar, para datos censurados, están disponibles extensiones bivariantes del estimador univariante de Kaplan-Meier de función de distribución. Por ejemplo, la versión presentada en (Dabrowska 1988) es atractiva. Sin embargo, debido a los casos en que aparecen grandes masas de datos en el rango superior de los datos, este y otros estimadores de la función de distribución bivariante no son fiables. Esto significa que las medidas resumidas de la función de distribución estimada basadas en la rho de Spearman o la tau de Kendall pueden no ser fiables. Para esta situación, la versión beta de Blomqvist parece ser una mejor opción, ya que se basa en el centro de la distribución. (Hougaard 2000), Capítulo 14, proporciona una discusión adicional.
Puede obtener la versión beta de Blomqvist utilizando la función betan() de la librería copula en R. A continuación se obtiene \(\beta=0,3\) entre la variable de tarificación Coverage en millones de dólares y la variable de cuantía Claim en dólares.
Código R para la Beta de Blomqvist
Además, para mostrar que la beta de Blomqvist es invariable bajo transformaciones estrictamente crecientes, \(\beta=0,3\) entre la variable de tarificación Coverage en logaritmo de millones de dólares y la variable de cuantía Claim en logaritmo de millones de dólares.
TS 14.A.2. Enfoque no paramétrico utilizando la correlación de Spearman con empates en los rangos
Para la primera variable, el rango promedio de las observaciones en la \(s\)ésima fila es
\[\begin{equation*} r_{1s} = n_{m_1\centerdot}+ \cdots+ n_{s-1,\centerdot}+ \frac{1}{2} \left(1+ n_{s\centerdot}\right) \end{equation*}\]
y similarmente \(r_{2t} = \frac{1}{2} \left[(n_{\centerdot m_1}+ \cdots+ n_{\centerdot,s-1}+1)+ (n_{\centerdot m_1}+ \cdots+ n_{\centerdot s})\right]\). Con esto tenemos que la rho de Spearman con empates en los rangos es
\[\begin{equation*} \hat{\rho}_S = \frac{\sum_{s=m_1}^{m_2} \sum_{t=m_1}^{m_2} n_{st}(r_{1s} - \bar{r})(r_{2t} - \bar{r})} {\left[\sum_{s=m_1}^{m_2}n_{s \centerdot}(r_{1s} - \bar{r})^2 \sum_{t=m_1}^{m_2} n_{\centerdot t}(r_{2t} - \bar{r})^2 \right]^2} \end{equation*}\]
donde el rango medio es \(\bar{r} = (n+1)/2\).
Haga clic para mostrar la prueba para un caso especial: datos binarios.
Puede obtener el estadístico de correlación de Spearman corregido por los empates \(r_S\) usando la función cor() en R y seleccionando el método spearman. A continuación se obtiene \(\hat{\rho}_S=-0,09\).