Chapter 12 Tarificación a posteriori usando Bonus-Malus
Este capítulo está siendo escrito y no está aún completo ni editado. Se presenta aquí para facilitar un avance de lo que aparecerá en la versión final.
12.1 Introducción
El Sistema Bonus-Malus, que es usado bajo otros sinónimos como “descuento por no culpa,” “tarificación por méritos,” “tarificación basada en la experiencia” o “descuento por no-siniestros” en diferentes países, está basado en la penalización a aquellos asegurados que son responsables de uno o más siniestros con un recargo en la prima, y la recompensa con un descuento en la prima a aquellos asegurados que no han tenido ningún siniestro. Las compañías aseguradoras usan los sistemas bonus-malus con dos propósitos fundamentales; para animar a los conductores a conducir de forma más prudente en un año sin siniestros, y para garantizar que los asegurados pagan primas proporcionales a sus riesgos en base a su experiencia en siniestralidad.
El Sistema Descuento por No Siniestros (NCD, según sus siglas en inglés) es un sistema de tarificación basado en la experiencia que es usado de forma muy frecuente en el seguro del automóvil. Su objetivo es categorizar a los asegurados en grupos homogéneos que pagan primas en base a su experiencia en siniestralidad. Dependiendo de las reglas del esquema, los nuevos tomadores pueden estar obligados a pagar la prima total al principio, y obtener descuentos en los años siguientes como consecuencia de no haber sufrido siniestros. Un sistema NCD recompensa a los tomadores por no sufrir siniestros durante un año, en otras palabras, gratifica con un bonus al buen conductor. El principio de bonus puede afectar a la decisión de los tomadores a la hora de declarar o no un siniestro, especialmente cuando están involucrados en siniestros leves, con daños pequeños, lo que se conoce como el fenómeno ‘hambre de bonus.’ La opción ‘hambre de bonus’ en un sistema NCD puede reducir los costes siniestrales de los aseguradores, y puede compensar la disminución esperada de los ingresos por primas.
12.2 Sistema NCD en Varios Países
12.2.1 Sistema NCD en Malasia
Antes de la liberalización de las tarifas de automóviles el 1 de julio de 2017, la tarificación del seguro de automóvil en Malasia estaba regulada por la Tarifa de Autos. Bajo esta tarifa, la prima cobrada no debía ser más baja que las primas especificadas para las diferentes clases de riesgos, para asegurar que la competencia de precios entre aseguradores no estuviese por debajo de lo que exigía el nivel económico del país. Los factores usados en la tarificación eran la cobertura del seguro, la capacidad cúbica del vehículo y el valor estimado del mismo (o suma asegurada, lo que fuera más bajo). Bajo la Tarifa de Autos, la prima final a pagar se ajustaba según la experiencia en siniestralidad del tomador, o equivalentemente, su categoría NCD. Con efecto 1 de julio de 2017, se liberaliza el cálculo de las primas del seguro del automóvil. El cálculo de las primas es a partir de entonces realizado por cada compañía aseguradora de forma individual y por los operadores takaful, y los clientes pueden disfrutar de una amplia oferta de seguros del automóvil a precios competitivos. La liberalización de tarifas potencia la innovación y la competencia entre aseguradores y operadores takaful, las primas se calculan en base a amplios conjuntos de factores de riesgos, más allá de los dos factores de riesgo usados en la Tarifa de Autos, es decir, la suma asegurada y la capacidad cúbica del vehículo. Otros factores usados en la tarificación pueden estar relacionados con el perfil de riesgo del asegurado, como la antigüedad del vehículo, la edad del conductor, las medidas de seguridad del vehículo, la localización geográfica del mismo, y las infracciones del conductor. Como las compañías aseguradoras y los operadores takaful pueden tener diferentes formas de definir el perfil de riesgo de un asegurado, la prima puede diferir de un asegurador a otro. Sin embargo, la estructura NCD existente en la Tarifa de Autos continúa existiendo ‘sin cambios,’ y es ‘transferible’ de un asegurador, o desde el operador takaful, a otro.
Los descuentos en el sistema NCD Malasio están divididos en seis clases, partiendo de la clase inicial con un 0% de descuento, seguida de clases con descuentos del 25%, 30%, 38,3%, 45% y 55%. La Tabla 1 proporciona las clases del sistema NCD en Malasia. Un año sin siniestros indica que el tomador puede moverse hacia la siguiente clase de descuento, por ejemplo del descuento 0% al descuento del 25% en el año de renovación. Si un tomador está ya en la clase más alta, a la que corresponde el descuento del 55%, un año sin siniestros supone que el tomador continuará en la misma clase. Por otro lado, si sufre uno o más siniestros dentro del año, perderá el NCD y el tomador tiene que empezar de nuevo con un 0% en el año de renovación. En otras palabras, el tomador ha de pagar la prima completa en la siguiente renovación anual, independientemente de su nivel NCD actual.
Con fines ilustrativos, la Figura 12.1 muestra el diagrama de transición entre clases NCD de la Tarifa de Autos Malasia. La transición empieza en la clase 0, y aumenta de una en una si el asegurado no ha tenido ningún siniestro por año. Si un asegurador tiene uno o más siniestros dentro del año, la clase actual vuelve automáticamente a la clase 0.
\[ \begin{matrix} \text{Tabla 1: Clases de NCD (Malasia)}\\ \begin{array}{*{20}c} \hline \text{Clases (años sin siniestros)} & \text{Descuentos}\\ \hline\\ {0} & {0}\\ {1} & {25}\\ {2} & {30}\\ {3} & {38,33}\\ {4} & {45}\\ {5\text{ y superiores}} & {55}\\\\ \hline \end{array} \end{matrix} \]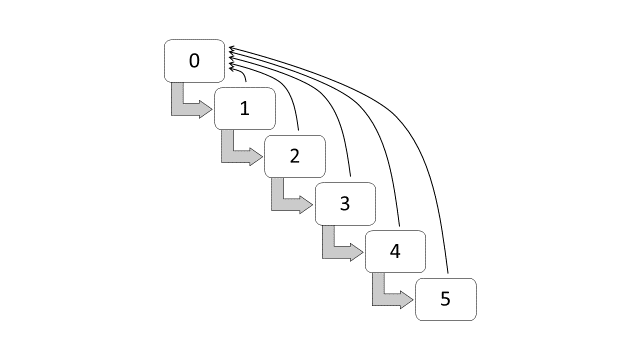
Figure 12.1: Diagrama de transición entre clases NCD (Malasia)
12.2.2 Sistema NCD en Otros Países
El sistema NCD en Brasil se subdivide en siete clases, con los siguientes niveles de primas (Lemaire 1998): 100, 90, 85, 80, 75, 70, y 65. Estos niveles de primas son también equivalentes a las siguientes clases de descuentos: 0%, 10%, 15%, 20%, 25%, 30% y 45%. Los tomadores nuevos comienzan con un descuento del 0%, o en el nivel 100, y si al cabo de un año no han tenido ningún siniestro se mueven a la siguiente clase de descuento. Si durante el año sufren uno o más siniestros, retroceden a la clase anterior de descuento. La Tabla 2 y la Figura 12.2 muestran respectivamente las clases y el diagrama de transición en el sistema NCD en Brasil.
\[ \begin{matrix} \text{Tabla 2: Clases de NCD (Brasil)}\\ \begin{array}{*{20}c} \hline \text{Clases (años sin siniestros)} & \text{Descuentos}\\ \hline\\ {0} & {0}\\ {1} & {10}\\ {2} & {15}\\ {3} & {20}\\ {4} & {25}\\ {5} & {30}\\ {6\text{ y superiores }} & {45}\\\\ \hline \end{array} \end{matrix} \]
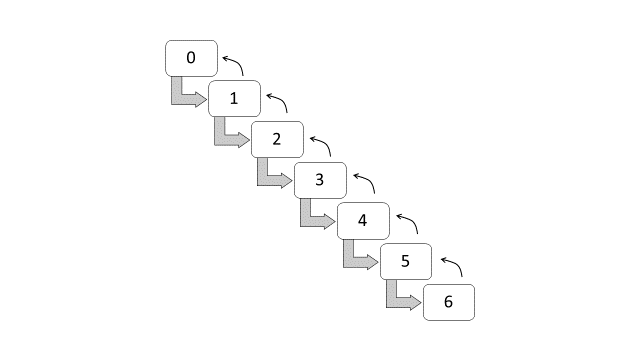
Figure 12.2: Diagrama de transición entre clases NCD (Brasil)
El sistema NCD en Suiza, implementado en 1990, está subdividido en veintidós clases, con los siguientes niveles de primas: 270, 250, 230, 215, 200, 185, 170, 155, 140, 130, 120, 110, 100, 90, 80, 75, 70, 65, 60, 55, 50 y 45 (Lemaire y Zi 1994). Estos niveles son también equivalentes a los siguientes recargos: 170%, 150%, 130%, 115%, 100%,85%, 70%, 55%, 40%, 30%, 20%, y 10%, y los siguientes descuentos: 0%,10%, 20%, 25%, 30%, 35%, 40%, 45%, 50% y 55%. Los tomadores nuevos comienzan con el nivel de recargo del 170%, o el nivel de prima 270, y tras un año sin siniestros se mueven hacia la siguiente clase de descuento. Si durante el año se producen uno o más siniestros, el tomador retrocede cuatro clases. La Tabla 3 y la Figura 12.3 muestran respectivamente las clases y el diagrama de transición para el sistema NCD en Suiza.
\[ \begin{matrix} \text{Tabla 3: Clases de NCD (Suiza)}\\ \begin{array}{*{20}c} \hline \text{Clases} & \text{Recargos} & \text{Clases} & \text{Descuentos}\\ \text{(años sin siniestros)} & & \text{(años sin siniestros)} & \\ \hline\\ {0} & {170} & {12} & {0}\\ {1} & {150} & {13} & {10}\\ {2} & {130} & {14} & {20}\\ {3} & {115} & {15} & {25}\\ {4} & {100} & {16} & {30}\\ {5} & {85} & {17} & {35}\\ {6} & {70} & {18} & {40}\\ {7} & {55} & {19} & {45}\\ {8} & {40} & {20} & {50}\\ {9} & {30} & {21 \text{ y superiores}} & {55}\\ {10} & {20} && \\ {11} & {10} && \\\\ \hline \end{array} \end{matrix} \]
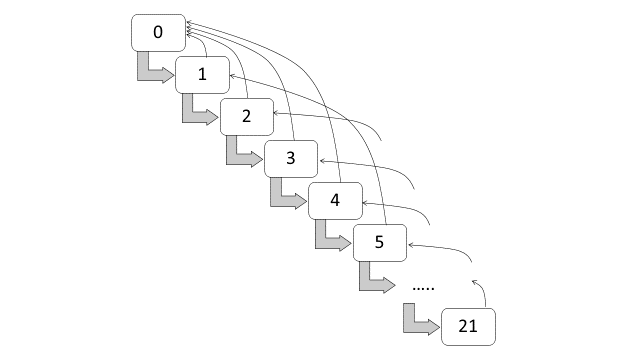
Figure 12.3: Diagrama de transición entre clases NCD (Suiza)
12.3 BMS y Modelo de Cadenas de Markov
Un sistema BMS, o sistema NCD, puede representarse por una cadena de Markov en tiempo discreto. En este caso, el modelo consta de clases de bonus-malus, y el estado (o clase) se supone que cambia aleatoriamente año a año. Por tanto, es importante realizar una breve descripción de dos conceptos relevantes; un proceso estocástico que posee una propiedad de Markov, y una cadena de Markov discreta en el tiempo.
Definición: Un proceso estocástico tiene una propiedad de Markov si la distribución de probabilidad de estados futuros, condicionada a los estados pasados y presentes, depende solo del estado actual y no de la secuencia de eventos que lo preceden.
Definición: Una cadena de Markov temporal discreta es un proceso estocástico que puede ser parametrizado mediante la estimación empírica de las probabilidades de transición entre estados discretos.
12.3.1 Probabilidad de Transición
La aleatoriedad de la transición entre clases depende de la probabilidad de transición en un año dado. La definición de la probabilidad de transición permite comprender aquí el uso de dicha probabilidad para representar la transición entre clases NCD.
Definición: La probabilidad de transición desde el estado \(i\) (en el momento \(n\)) al estado \(j\) (en el momento \(n + 1\)) se denomina probabilidad de transición temporal uno, y se escribe como \(p_{ij} = Pr (X_{n + 1} = j|X_n = i)\), \(i = 1,2,...,k\), \(j = 1,2,...,k\).
Las probabilidades de transición pueden representarse por una matriz \(k \times k\). Asumiendo un proceso de Markov homogéneo, una cadena de Markov para k-estados puede representarse por una matriz de probabilidades de transición \({\bf P}\):
\[ {\bf P} = \left[ {\begin{array}{*{20}c} p_{11} & p_{12} & \ldots & & & p_{1k} \\ p_{21} & p_{22} & \ldots & & & p_{2k} \\ \vdots & \ddots & & & & \vdots \\ & & & & & \\ & & & & & \\ p_{k1} & p_{k2} & \cdots & & & p_{kk} \end{array} } \right]. \]
Cada fila de la matriz de transición representa la transición entre un estado y el resto, mientras que cada columna representa la transición desde diferentes estados a uno determinado. Las transiciones acumuladas desde un estado hacia los demás debe ser igual a 1, es decir, cada fila de la matriz debe sumar 1, y por tanto \(\sum\limits_j p_{ij} = 1\). Todas las probabilidades deben ser también no negativas (ya que son probabilidades), por tanto \(p_{ij} \ge 0\).
Consideremos el sistema NCD de Malasia. Bajo este sistema, sea la variable aleatoria \(X_t\) la que indica la clase NCD en el momento \(t\) con valores en el espacio definido por el conjunto de estados \(\bf{S}\), donde \({\bf S} = \{0,1,...,5\}\). Por tanto, la probabilidad para un año sin siniestros es igual a la probabilidad de transición desde el estado \(i\) al estado \(j\), que es \(p_{ij}\), \(i = 0,1,2,...,5\), \(j = 0,1,2,...,5\). Si un asegurado tiene uno o más siniestros dentro del año, la probabilidad de transición de volver al estado 0 se representa por \(p_{i0}\), que es también equivalente a \(1 - {p_{ij}}.\) Por tanto, hay solo dos probabilidades de transición en cada fila ; la probabilidad de avanzar al siguiente estado , \(p_{ij},\) y la probabilidad de retornar al estado cero , \(p_{i0} = 1 - p_{ij}\).
En términos de las probabilidades de transición, el sistema NCD de Malasia puede representarse por la siguiente matriz de transición \((6 \times 6)\):
\[ {\bf P} = \left[ {\begin{array}{*{20}c} p_{00}&p_{01}&0&0&0&0\\ p_{10}&0&p_{12}&0&0&0\\ p_{20}&0&0&p_{23}&0&0\\ p_{30}&0&0&0&p_{34}&0\\ p_{40}&0&0&0&0&p_{45}\\ p_{50}&0&0&0&0&p_{55} \end{array} }\right] = \left[ {\begin{array}{*{20}c} {1 - p_{01}}&p_{01}&0&0&0&0\\ {1 - p_{12}}&0&p_{12}&0&0&0\\ {1 - p_{23}}&0&0&p_{23}&0&0\\ {1 - p_{34}}&0&0&0&p_{34}&0\\ {1 - p_{45}}&0&0&0&0&p_{45}\\ {1 - p_{55}}&0&0&0&0&p_{55} \end{array} }\right] \]
Ejemplo 1
Proporciona la matriz de transición para el sistema NCD en Brasil.
Solución
Teniendo en cuenta las clases NCD y el diagrama de transición mostrados respectivamente en la Tabla 2 y Figura 12.2, la probabilidad para un año sin siniestro es igual a la probabilidad de moverse una clase hacia delante, mientras que la probabilidad de tener uno o más siniestros dentro del año es igual a la probabilidad de moverse una clase hacia atrás. Por tanto, cada fila puede contener dos o más probabilidades de transición; una probabilidad para avanzar hacia la siguiente clase, y una o más probabilidades de moverse una clase hacia atrás. La matriz de transición es:
\[ {\bf P} = \left[ {\begin{array}{*{20}{c}} {1 - p_{01}}&p_{01}&0&0&0&0&0\\ {1 - p_{12}}&0&p_{12}&0&0&0&0\\ {1 - \sum\limits_j p_{2j}}&p_{21}&0&p_{23}&0&0&0\\ {1 - \sum\limits_j p_{3j}}&p_{31}&p_{32}&0&p_{34}&0&0\\\ {1 - \sum\limits_j p_{4j}}&p_{41}&p_{42}&p_{43}&0&p_{45}&0\\ {1 - \sum\limits_j p_{5j}}&p_{51}&p_{52}&p_{53}&p_{54}&0&p_{56}\\ {1 - \sum\limits_j p_{6j}}&p_{61}&p_{62}&p_{63}&p_{64}&p_{65}&p_{66} \end{array} } \right] \]
Ejemplo 2
Proporciona la matriz de transición para el sistema NCD en Suiza.
Solución
A partir de la Tabla 3 y de la Figura 12.3, la probabilidad de un año sin siniestro es igual a la probabilidad de moverse una clase hacia delante, mientras que la probabilidad de tener uno o más siniestros dentro del año es igual a la probabilidad de moverse cuatro clases hacia atrás. La matriz de transición es:
\[ \begin{matrix} \left| {\begin{array}{*{12}{c}} 1 - {p_{01}} & p_{01} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{12}} & 0 & p_{12} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{23}} & 0 & 0 & p_{23} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{34}} & 0 & 0 & 0 & p_{34} & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - {p_{45}} & 0 & 0 & 0 & 0 & p_{45} & 0 & 0 & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{5j}} & p_{51} & 0 & 0 & 0 & 0 & p_{56} & 0 & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{6j}} & 0 & p_{62} & 0 & 0 & 0 & 0 & p_{67} & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{7j}} & 0 & 0 & p_{73} & 0 & 0 & 0 & 0 & p_{78} & 0 & 0 & \cdots\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots\\ 1 - \sum\limits_j {p_{19,j}} & 0 & 0 & p_{19,3} & 0 & 0 & 0 & p_{19,7} & 0 & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{20,j}} & 0 & 0 & 0 & p_{20,4} & 0 & 0 & 0 & p_{20,8} & 0 & 0 & \cdots\\ 1 - \sum\limits_j {p_{21,j}} & p_{21,1} & 0 & 0 & 0 & p_{21,5} & 0 & 0 & 0 & p_{21,9} & 0 & \cdots \end{array}} \right| \end{matrix} \]
12.4 BMS y Distribución Estacionaria
12.4.1 Distribución Estacionaria
Es importante destacar que la matriz de transición representa las probabilidades de transición de las clases NCD en un año. Si estamos interesados en la distribución de la transición en el largo plazo (que puede suponer varios años), puede usarse la probabilidad estacionaria.
Presentamos varias definiciones y propiedades para comprender el uso del modelo de cadenas de Markov para representar la distribución estacionaria de las transiciones NCD. Sin embargo, se anima a los estudiantes a recurrir a textos sobre Cadenas de Markov y procesos estocásticos disponibles en la literatura para una mayor comprensión de los conceptos presentados.
Definición: Una cadena de Markov se dice que es irreducible si es posible pasar a un estado desde otro estado.
Definición: Un estado \(i\) tiene periodo \(k\) si cualquier retorno al estado \(i\) se produce en múltiplos de \(k\) periodos de tiempo. Si \(k = 1\), entonces se dice que el estado es aperiódico.
Definición: Un estado \(i\) se dice que es transitorio si, teniendo en cuenta que empezamos en el estado \(i\), existe un probabilidad diferente de cero de no volver nunca a \(i\). El estado \(i\) es recurrente (o persistente) si no es transitorio. Un estado \(i\) es recurrente positivo si el tiempo de recurrencia medio (o tiempo esperado de retorno) es finito.
Definición: Un estado \(i\) se dice que es ergódico si es aperiódico y recurrente positivo. En otras palabras, un estado \(i\) es ergódico si es recurrente, tiene un periodo de uno (aperiódico), y tiene tiempo de recurrencia medio finito. Si todos los estados en una cadena de Markov irreducible son ergódicos, entonces se dice que la cadena es ergódica.
Definición: Sea \(p_{ij}^{(n)} = \Pr ({X_n} = j\|{X_0} = i)\) la probabilidad de transición desde el estado \(i\) al estado \(j\) en \(n\) periodos de tiempo. Las probabilidades de transición n-pasos para una cadena de Markov estacionaria satisfacen la ecuación de Chapman–Kolmogorov: \[p_{ij}^{(n)} = \sum\limits_r {p_{ir}^{(k)}p_{rj}^{(n - k)}}\] Para cualquier \(k\), donde \(0 < k < n\).
Definición: Si una cadena de Markov es estacionaria, entonces el vector \({\bf{\pi }}\) se denomina distribución estacionaria (or medida invariante) si satisface:
\[0 \le {\pi _j} \le 1\]
\[\sum\limits_j {{\pi _j}} = 1,\]
\[{\pi_j} = \sum\limits_i {\pi_i}p_{ij}\].
En términos de vectores y matrices, una distribución estacionaria \({\bf{\pi }}\) es un vector fila, cuyas entradas son no negativas y suman uno, que no cambia con la operación:
\({\bf{\pi P}} = {\bf{\pi }}\).
Si una cadena de Markov es estacionaria, entonces la matriz de transición \({\bf{P}}\) es la misma después de cada paso, de forma que la probabilidad de transición en el paso \(k\) puede calcularse como el valor de la matriz de transición elevado a \(k\), \({{\bf{P}}^k}.\)
A partir de las definiciones y propiedades anteriores, un sistema BMS sigue una cadena regular de Markov si todos sus estados (clases NCD) son ergódicos, y la cadena es no cíclica (o irreversible). El vector fila, \({\bf{\pi }}\), que es también el vector propio izquierdo de la matriz de transición, es una distribución estacionaria definida por \(0 \le {\pi _j} \le 1\) y \(\sum\limits_j {{\pi_j}} = 1\).
Ejemplo 3
Encuentra la distribución estacionaria para el sistema NCD en Malasia asumiendo que las probabilidades de un año sin siniestros para todas las clases NCD son \({p_0}\).
Solución
La matriz de transición puede reescribirse como:
La distribución estacionaria puede calcularse usando \({\pi _j} = \sum\limits_i {\pi _i}p_{ij}\). Las soluciones son:
\[ \begin{array}{l} {\pi _0} = \sum\limits_i {\pi_i}p_{i0} = (1 - {p_0})\sum\limits_i {{\pi _i}} = 1 - {p_0}\\\\ {\pi _1} = \sum\limits_i {\pi _i}p_{i1} = {\pi_0}{p_{01}} = (1 - {p_0}){p_0}\\\\ {\pi _2} = \sum\limits_i {\pi _i}p_{i2} = {\pi _1}{p_{12}} = (1 - {p_0}){p_0}^2\\\\ {\pi _3} = \sum\limits_i {\pi _i}p_{i3} = {\pi _2}{p_{23}} = (1 - {p_0}){p_0}^3\\\\ {\pi _4} = \sum\limits_i {\pi _i}p_{i4} = {\pi _3}{p_{34}} = (1 - {p_0}){p_0}^4\\\\ {\pi _5} = \sum\limits_i {\pi _i}p_{i5} = {\pi _4}{p_{45}} + {\pi _5}{p_{55}} = (1 - {p_0}){p_0}^5 + {\pi _5}{p_0}\\\\ \therefore {\pi _5} = \frac{(1 - {p_0}){p_0}^5}{{(1 - {p_0})}} = {p_0}^5 \end{array} \]
La distribución estacionaria (o condición de estado estacionario) mostrada en el Ejemplo 3 representa la distribución asintótica del sistema NCD, o la distribución en el largo plazo. Como ejemplo, asumiendo que la probabilidad de un año sin siniestros es \(p_0 = 0,90,\) las probabilidades estacionarias son:
\[ \begin{array}{l} {\pi _0} = 1 - {p_0} = 0,1000\\\\ {\pi _1} = (1 - {p_0}){p_0} = 0,0900\\\\ {\pi _2} = (1 - {p_0}){p_0}^2 = 0,0810\\\\ {\pi _3} = (1 - {p_0}){p_0}^3 = 0,0729\\\\ {\pi _4} = (1 - {p_0}){p_0}^4 = 0,0656\\\\ {\pi _5} = {p_0}^5 = 0,5905 \end{array} \]
En otras palabras, \({\pi_0} = 0,10\) indica que el 10% de los asegurados pertenecerán finalmente a la clase 0 (o cero años sin siniestros), \({\pi _1} = 0,09\) indica que el 9% de los asegurados pertenecerán finalmente a la clase 1 (o un año sin siniestros), y así sucesivamente, hasta \({\pi _5} = 0,59\), que indica que el 59% de los asegurados pertenecerán finalmente a la clase 5 (o 5 años sucesivos sin siniestros).
12.4.2 Programa R para Distribuciones Estacionarias
Podemos usar el vector propio izquierdo de una matriz de transición para calcular la distribución estacionaria. El siguiente programa en R permite calcular el vector propio izquierdo:
#crear una matriz de transición
entries=c(0.1,0.9,0,0,0,0,
+ 0.1,0,0.9,0,0,0,
+ 0.1,0,0,0.9,0,0,
+ 0.1,0,0,0,0.9,0,
+ 0.1,0,0,0,0,0.9,
+ 0.1,0,0,0,0,0.9)
TP=matrix(entries,nrow=6,byrow=TRUE)
TP## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.1 0.9 0.0 0.0 0.0 0.0
## [2,] 0.1 0.0 0.9 0.0 0.0 0.0
## [3,] 0.1 0.0 0.0 0.9 0.0 0.0
## [4,] 0.1 0.0 0.0 0.0 0.9 0.0
## [5,] 0.1 0.0 0.0 0.0 0.0 0.9
## [6,] 0.1 0.0 0.0 0.0 0.0 0.9#calcular vector propio izquierdo
#Aviso – El vector propio izquierdo coincide con el vector propio derecho de la traspuesta de la propia matriz de transición (t(TP))
#dividir la entrada de la primera columna entre la suma de elementos, de tal manera que las entradas sumen 1
#proveer resultados con 4 decimales
round(eigen(t(TP))$vectors[,1]/sum(eigen(t(TP))$vectors[,1]),4)## [1] 0.1000+0i 0.0900+0i 0.0810+0i 0.0729+0i 0.0656+0i 0.5905+0iEjemplo 4
Encontrar la distribución estacionaria para el sistema NCD en Brasil asumiendo que el número de años sucesivos de siniestros se distribuye según una Poisson con parámetro \(\lambda = 0,10\).
Solución
Bajo la distribución de Poisson, la probabilidad de \(k\) años sucesivos de siniestros es \(p_k = \frac{e^{ - 0,1}{(0,1)}^k}{{k!}},{\rm{ }}k = 0,1,2,.....\)
La matriz de transición es:
\[ {\small {\bf{P}} = \left[ {\begin{array}{*{20}{c}} {1 - {p_0}}&{{p_0}}&0&0&0&0&0\\\\ {1 - {p_0}}&0&{{p_0}}&0&0&0&0\\\\ {1 -\sum\limits_i {{p_i}} }&{{p_1}}&0&{{p_0}}&0&0&0\\\\ {1 -\sum\limits_i {{p_i}} }&{{p_2}}&{{p_1}}&0&{{p_0}}&0&0\\\\ {1 - \sum\limits_i {{p_i}}}&{{p_3}}&{{p_2}}&{{p_1}}&0&{{p_0}}&0\\\\ {1 - \sum\limits_i{{p_i}} }&{{p_4}}&{{p_3}}&{{p_2}}&{{p_1}}&0&{{p_0}}\\\\ {1 - \sum\limits_i {{p_i}}}&{{p_5}}&{{p_4}}&{{p_3}}&{{p_2}}&{{p_1}}&{{p_0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0,0952}&{0,9048}&0&0&0&0&0\\\\ {0,0952}&0&{0,9048}&0&0&0&0\\\\ {0,0047}&{0,0905}&0&{0,9048}&0&0&0\\\\ {0,0002}&{0,0045}&{0,0905}&0&{0,9048}&0&0\\\\ {0,0000}&{0,0002}&{0,0045}&{0,0905}&0&{0,9048}&0\\\\ {0,0000}&{0,0000}&{0,0002}&{0,0045}&{0,0905}&0&{0,9048}\\\\ {0,0000}&{0,0000}&{0,0000}&{0,0002}&{0,0045}&{0,0905}&{0,9048} \end{array}}\right]} \]
Usando el programa R, las probabilidades estacionarias son: \[ \left[ {\begin{array}{*{20}{c}} {{\pi _0}}\\\\ {{\pi_1}}\\\\ {{\pi _2}}\\\\ {{\pi _3}}\\\\ {{\pi _4}}\\\\ {{\pi_5}}\\\\ {{\pi _6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0,0000}\\\\ {0,0000}\\\\ {0,0003}\\\\ {0,0022}\\\\ {0,0145}\\\\ {0,0936}\\\\ {0,8894} \end{array}} \right] \]
Las probabilidades indican que el 89% de los asegurados pertenecerán finalmente a la clase 6 (seis años sucesivos libres de siniestros), 9% de los asegurados pertenecerán finalmente a la clase 5 (cinco años sucesivos libres de siniestros), y un 1,5% de los asegurados pertenecerán finalmente a la clase 4 (cuatro años sucesivos libres de siniestros). Otras clases, una vez combinadas, tienen menos del 1% de los asegurados.
Ejemplo 5
Usando los resultados del Ejemplo 4, encuentra la prima final bajo la condición de equilibrio asumiendo que la prima anterior a la implementación del sistema NCD es \(m.\)
Solución
Usando las probabilidades estacionarias del Ejemplo 4, la prima final estacionaria es:
\[ \begin{array}{l} = \sum\limits_j \text{(prima)} \times \text{(proporción en clase } j \text{ en el largo plazo)} \times \text{(1 - NCD en la clase } j)\\\\ = m[{\pi _0}(1) + {\pi _1}(1 – 0,9) + {\pi _2}(1 – 0,15) + \ldots + {\pi _6}(1 – 0,35)]\\\\ = m[0 + 0 + (0,0003)(0,85) + \ldots + (0,8894)(0,65)]\\\\ = 0,6565m \end{array} \]
Los resultados indican que la prima final disminuye desde m a 0,6565m en el largo plazo (bajo la condición de equilibrio o la condición estacionaria) si se considera el NCD.
12.4.3 Evolución de la Prima
Algunas veces estamos interesados en observar la evolución de la prima media después de \(n\) años (o \(n\) pasos). Bajo el sistema NCD, puede usarse la probabilidad de transición en n-pasos, \(p_{ij}^{(n)}\), para observar la evolución de la prima media. Presentamos una definición de la probabilidad de transición en n-pasos \(p_{ij}^{(n)}\) para comprender el uso de la probabilidad con el objetivo de observar la evolución de la prima media.
Definición: Sea \(p_{ij} = \Pr ({X_{n + 1}} = j|{X_n} = i)\) la probabilidad de transición en un paso desde el estado \(i\) al estado \(j\), y \(p_{ij}^{(n)} = \Pr ({X_n} = j|{X_0} = i)\), \(n = 1,2,...\), la probabilidad de transición en n-pasos desde el estado \(i\) al estado \(j\). Podemos obtener la probabilidad \(p_{ij}^{(n)}\) usando la enésima potencia de la matriz de transición \({\bf{P}}\), que es \({\bf{P}^n}.\)
Ejemplo 6
Observad las primas en 20 años bajo el sistema NCD en Malasia, asumiendo que la probabilidad de siniestros sigue una distribución de Poisson con parámetro \(\lambda = 0,10\) y la prima anterior a la implementación del NCD es \(m = 100\).
Solución
Bajo el sistema Malasio NCD, usamos la probabilidad de Poisson, \(p_k = \frac{e^{ - 0,1}{(0,1)}^k}{k!}\), solo para \(k = 0,1.\) Por tanto, la matriz de transición en el primer año es:
\[ {\bf{P}^{(1)}} = \left[{\begin{array}{*{20}{c}} {0,0952}&{0,9048}&0&0&0&0\\\\ {0,0952}&0&{0,9048}&0&0&0\\\\ {0,0952}&0&0&{0,9048}&0&0\\\\ {0,0952}&0&0&0&{0,9048}&0\\\\ {0,0952}&0&0&0&0&{0,9048}\\\\ {0,0952}&0&0&0&0&{0,9048} \end{array}} \right] \]
La prima en el primer año, después de implementar el NCD, es:
\[ \begin{aligned} &= \sum\limits_j \text{(prima)} \times \text{(proporción media en la clase } j) \times \text{(1 - NCD en la clase }j) \\ &= m\left[ \frac{\sum\limits_i {p_{i0}}}{6}{(1)} + \frac{\sum\limits_i {p_{i1}}}{6}{(1 – 0,25)} + \ldots + \frac{\sum\limits_i {p_{i5}}}{6}{(1 – 0,55)} \right]\\ &= 100[0,0952(1) + 0,1508(0,75) + \cdots + 0,3016(0,45)]\\ &= 62,55. \end{aligned} \]
Usando pasos similares, podemos observar la prima en el año \(n\)- con \(n = 1,2,...,20\) . Usando el programa R, las primas en los 20 años son :
62,55, 59,87, 58,06, 57,06, 56,58, 56,58, 56,58, 56,58, 56,58, 56,58,
56,58, 56,58, 56,58, 56,58, 56,58, 56,58, 56,58, 56,58, 56,58, 56,58.
12.4.4 Programa R para la evolución de las Primas
El siguiente programa R puede usarse para encontrar la prima en el año n y las primas en los 20 años bajo el sistema NCD en Malasia (para encontrar la solución en el Ejemplo 6).
#crear la matriz de transición
entries=c(0.0952,0.9048,0,0,0,0,
+ 0.0952,0,0.9048,0,0,0,
+ 0.0952,0,0,0.9048,0,0,
+ 0.0952,0,0,0,0.9048,0,
+ 0.0952,0,0,0,0,0.9048,
+ 0.0952,0,0,0,0,0.9048)
TP=matrix(entries,nrow=6,byrow=TRUE)
TP## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.0952 0.9048 0.0000 0.0000 0.0000 0.0000
## [2,] 0.0952 0.0000 0.9048 0.0000 0.0000 0.0000
## [3,] 0.0952 0.0000 0.0000 0.9048 0.0000 0.0000
## [4,] 0.0952 0.0000 0.0000 0.0000 0.9048 0.0000
## [5,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048
## [6,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048#crear la función para la n-ésima potencia de la matriz cuadrada
powA = function(n) {
if (n==1) return (TP)
if (n==2) return (TP%*%TP)
if (n>2) return ( TP%*%powA(n-1)) }
#ejemplo para n=3
powA(3)## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.0952 0.08613696 0.07793672 0.7407263 0.0000000 0.0000000
## [2,] 0.0952 0.08613696 0.07793672 0.0000000 0.7407263 0.0000000
## [3,] 0.0952 0.08613696 0.07793672 0.0000000 0.0000000 0.7407263
## [4,] 0.0952 0.08613696 0.07793672 0.0000000 0.0000000 0.7407263
## [5,] 0.0952 0.08613696 0.07793672 0.0000000 0.0000000 0.7407263
## [6,] 0.0952 0.08613696 0.07793672 0.0000000 0.0000000 0.7407263#definir el porcentaje NCD
NCD=c(1,.75,.7,.6167,.55,.45)
#crear la función para la prima en el año n
p=numeric(0)
prem=function(n){
for (j in 1:length(NCD))
p[j]=mean(powA(n)[,j])
+ 100*sum(p*NCD)}
#ejemplo para n=3
prem(3)## [1] 58.06106#calcular primas para 20 años
premium=numeric(0)
for (n in 1:20)
premium[n]=prem(n)
round(premium,2)## [1] 62.55 59.87 58.06 57.06 56.58 56.58 56.58 56.58 56.58 56.58 56.58 56.58
## [13] 56.58 56.58 56.58 56.58 56.58 56.58 56.58 56.58Ejemplo 7
Observar las primas durante 20 años bajo el sistema NCD en Brasil, asumiendo que la probabilidad de \(k\) años sucesivos de siniestros es \(p_k = \frac{e^{ - 0,1}{(0,1)}^k}{{k!}},{\rm{ }}k = 0,1,2,.....\), y la prima anterior a la implementación del sistema NCD es \(m = 100\).
Solución
La matriz de transición para el sistema NCD en Brasil es: \[ {\bf P} = \left[ {\begin{array}{*{20}{c}} {0,0952}&{0,9048}&0&0&0&0&0\\\\ {0,0952}&0&{0,9048}&0&0&0&0\\\\ {0,0047}&{0,0905}&0&{0,9048}&0&0&0\\\\ {0,0002}&{0,0045}&{0,0905}&0&{0,9048}&0&0\\\\ {0,0000}&{0,0002}&{0,0045}&{0,0905}&0&{0,9048}&0\\\\ {0,0000}&{0,0000}&{0,0002}&{0,0045}&{0,0905}&0&{0,9048}\\\\ {0,0000}&{0,0000}&{0,0000}&{0,0002}&{0,0045}&{0,0905}&{0,9048} \end{array}} \right] \]
Usando el programa R las primas en 20 años son:
76,69, 73,76, 71,31, 69,38, 67,92, 66,93, 66,40, 66,05, 65,88, 65,78,
65,72, 65,69, 65,67, 65,66, 65,66, 65,66, 65,66, 65,65, 65,65, 65,65.
Los resultados en los ejemplos 6-7 nos permiten observar la evolución de la prima para los sistemas NCD en Malasia y Brasil asumiendo que el número de años sucesivos de siniestros se distribuye según una Poisson con parámetro \(\lambda = 0,10\), y la prima anterior a implementar el sistema NCD es \(m = 100\). La evolución de las primas para ambos países aparecen en la Tabla 4, y se muestran gráficamente en la Figura 12.4.
\[ \begin{matrix} \text{Tabla 4: Evolución de la prima (Malasia y Brasil)}\\ \begin{array}{*{20}c} \hline \text{año} & \text{prima} & \text{prima} & \text{año} & \text{prima} & \text{prima} & \\ & \text{Malasia} & \text{Brasil} & & \text{Malasia} & \text{Brasil} \\ \hline\\ 0 & 100 & 100 & 11 & 56,58 & 65,72 \\ 1 & 62,55 & 76,69 & 12 & 56,58 & 65,69 \\ 2 & 59,87 & 73,76 & 13 & 56,58 & 65,67 \\ 3 & 58,06 & 71,31 & 14 & 56,58 & 65,66 \\ 4 & 57,06 & 69,38 & 15 & 56,58 & 65,66 \\ 5 & 56,58 & 67,92 & 16 & 56,58 & 65,66 \\ 6 & 56,58 & 66,93 & 17 & 56,58 & 65,66 \\ 7 & 56,58 & 66,40 & 18 & 56,58 & 65,65 \\ 8 & 56,58 & 66,05 & 19 & 56,58 & 65,65 \\ 9 & 56,58 & 65,88 & 20 & 56,58 & 65,65 \\\\ \hline \end{array} \end{matrix} \]
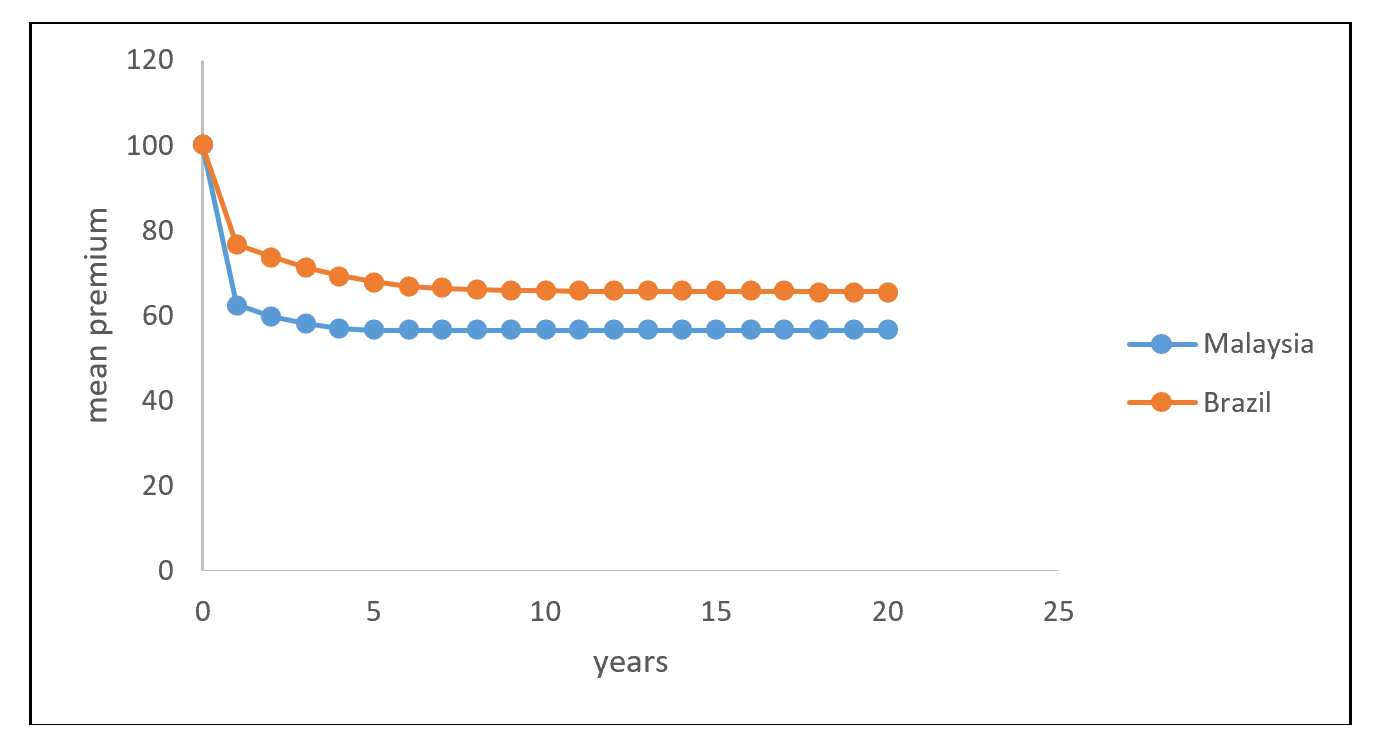
Figure 12.4: Evolución de la prima (Malasia y Brasil)
12.4.5 Ratio de Convergencia
Algunas veces estamos interesados en conocer la variación entre la probabilidad en el año n, \(p_{ij}^{(n)}\), y la probabilidad estacionaria, \(\pi _j\). La variación entre probabilidades puede medirse usando:
\[\left| {average(p_{ij}^{(n)}) - {\pi _j}} \right|\].
Por tanto, la variación total puede ser medida a partir de la suma de la variación en todas las clases:
\[\sum\limits_j {\left| {average(p_{ij}^{(n)}) - {\pi _j}} \right|}\].
La variación total se denomina también ratio de convergencia porque mide el ratio de convergencia después de \(n\) años (o \(n\) transiciones).
Ejemplo 8
Calcula las variaciones totales (ratio de convergencia) en 20 años bajo el sistema NCD en Malasia, asumiendo que la probabilidad de los siniestros se distribuye según una Poisson con parámetro \(\lambda = 0,10\).
Solución
Usando el programa R, las probabilidades estacionarias son:
\[ \left[ {\begin{array}{*{20}{c}} {{\pi _0}}\\\\{{\pi_1}}\\\\{{\pi _2}}\\\\ {{\pi _3}}\\\\{{\pi _4}}\\\\{{\pi_5}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0,0952}\\\\{0,0861}\\\\{0,0779}\\\\ {0,0705}\\\\{0,0638}\\\\{0,6064} \end{array}} \right] \]
La matriz de transición en el primer año es:
\[ {\bf{P}}^{(1)} = \left[ {\begin{array}{*{20}{c}} {0,0952}&{0,9048}&0&0&0&0\\\\ {0,0952}&0&{0,9048}&0&0&0\\\\ {0,0952}&0&0&{0,9048}&0&0\\\\ {0,0952}&0&0&0&{0,9048}&0\\\\ {0,0952}&0&0&0&0&{0,9048}\\\\ {0,0952}&0&0&0&0&{0,9048} \end{array}} \right] \]
La variación puede calcularse como: \[ \begin{array}{l} \left| {\sum\limits_i {\frac{p_{i0}^{}}{6}} - {\pi _0}} \right| = 0\\\\ \left|{\sum\limits_i {\frac{p_{i1}^{}}{6}} - {\pi _1}} \right| = 0,0647\\\\ \vdots \\\\ \left| {\sum\limits_i \frac{p_{i5}}{6} - {\pi _5}} \right| = ,3048 \end{array} \]
Por tanto, la variación total en el primer año es \(\sum\limits_j {\left| {\sum\limits_i {\frac{p_{ij}}{6} - {\pi _j}} } \right|} = 0,6096\).
Usando R, las variaciones totales (o ratio de convergencia) en 20 años son: 0,6096, 0,3941, 0,2252, 0,0958, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.
12.4.6 Programa R para el Ratio de Convergencia
El siguiente programa R puede usarse para calcular la variación total en el año n , y las variaciones totales (ratios de convergencia) en 20 años bajo el sistema NCD en Malasia (la solución en el Ejemplo 8).
#matriz de transición
TP## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.0952 0.9048 0.0000 0.0000 0.0000 0.0000
## [2,] 0.0952 0.0000 0.9048 0.0000 0.0000 0.0000
## [3,] 0.0952 0.0000 0.0000 0.9048 0.0000 0.0000
## [4,] 0.0952 0.0000 0.0000 0.0000 0.9048 0.0000
## [5,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048
## [6,] 0.0952 0.0000 0.0000 0.0000 0.0000 0.9048# probabilidad estacionaria
SP=eigen(t(TP))$vectors[,1]/sum(eigen(t(TP))$vectors[,1])
SP## [1] 0.09520000+0i 0.08613696+0i 0.07793672+0i 0.07051715+0i 0.06380391+0i
## [6] 0.60640526+0i#crear la función para la variación total en el año n
TV=function(n)
{dif=numeric(0)
for (j in 1:length(SP))
dif[j]=abs(mean(powA(n)[,j])-SP[j])
+ sum(dif)}
#ejemplo para n=1
TV(1)## [1] 0.6096105#calcular las variaciones totales (ratio de convergencia) en 20 años
tot.var=numeric(0)
for (n in 1:20)
tot.var[n]=TV(n)
round(tot.var,4)## [1] 0.6096 0.3941 0.2252 0.0958 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
## [11] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000Ejemplo 9
Calcular las variaciones totales (o ratio de convergencia) en 20 años bajo el sistema NCD en Brasil, asumiendo que el número de años sucesivos de siniestros se distribuye según una Poisson con parámetro \(\lambda = 0,10\)
Solución
Usando el programa R, las variaciones totales (o ratios de convergencia) en 20 años para el sistema NCD en Brasil son:
1,2617, 1,0536, 0,8465, 0,6412, 0,4362, 0,2316, 0,1531, 0,0747, 0,0480, 0,0232,
0,0145, 0,0071, 0,0043, 0,0021, 0,0013, 0,0006, 0,0004, 0,0002, 0,0001, 0,0001.
Los ejemplos 8-9 proporcionan el grado de convergencia para dos BMS diferentes (dos países diferentes). El BMS Malasio es totalmente estacionario solo después de cuatro años, mientras que el BMS en Brasil requiere un mayor periodo de tiempo. Como se menciona en Lemaire (1998), un BMS más sofisticado convergería más lentamente, lo que supone un inconveniente porque requiere más tiempo para ser estable. El principal objetivo de un BMS es separar los buenos de los malos conductores, y de este modo, es deseable tener un proceso de clasificación que pueda ser finalizado (o se estabilice) lo antes posible.
12.5 BMS y Tarificación de Primas
12.5.1 Tarificación de Primas
La tarificación de las Primas es el proceso mediante el cual se establecen los ratios de primas en el sistema asegurador, o en otros mecanismos de transferencia de riesgos. El proceso incluye un número de consideraciones como métodos estadísticos, objetivos de marketing, y restricciones legales y de competencia. La tarificación de las Primas debe cumplir cuatro objetivos básicos generalmente aceptados entre los actuarios; obtener primas “justas” de forma que los asegurados de riesgo alto paguen las primas más altas y viceversa, proporcionar reservas suficientes para pagar las pérdidas que puedan producirse y los gastos, proporcionar el margen adecuado para las desviaciones adversas, y generar retornos razonables a los aseguradores.
Antes discutíamos la aplicación del BMS en la tarificación de primas, ahora presentamos una breve discusión de los modelos de regresión binomial negativo y de Poisson. La regresión Poisson ha sido ampliamente usada para ajustar datos de conteo (o frecuencias) en seguros. La regresión binomial negativa puede usarse para ajustar datos de conteo (o frecuencias) con sobredispersión, situación que se produce cuando la varianza es superior a la media. Se anima a los estudiantes a consultar libros sobre GLM o sobre modelos de regresión disponibles en la literatura para profundizar en el conocimiento de los temas tratados.
12.5.2 Modelos de Frecuencia – Regresiones de Poisson y Binomial Negativa
Sea \({({Y_1},{Y_2},...,{Y_n})^T}\) un vector de variables aleatorias de conteo y \(n\) el tamaño muestral. La p.m.f. (función de cuantía, de probabilidad o de masa de probabilidad, según sus siglas en inglés) para el modelo de regresión de Poisson es,
\[\Pr ({Y_i} = {y_i}) \begin{array}{*{20}{c}} = \frac{{{\exp(- {\mu _i})}{\mu _i}^{y_i}}}{y_i{!}}&{y_i = 0,1,...} \end{array} \]
Con media y varianza \(E({Y_i}) = Var({Y_i}) = {\mu _i}\).
Para tener en cuenta los valores no-negativos, la media, o el valor ajustado, se asume que sigue un enlace logarítmico, \(E({Y_i}) = {\mu _i} = \exp ({\bf x}_{\bf i}{\bf '\beta })\), donde \({\bf{x}}_{\bf i}\) indica el vector de variables explicativas y \({\bf \beta}\) es el vector de parámetros de la regresión . Los estimadores máximo verosímiles pueden obtenerse maximizando la función de log verosimilitud.
La p.m.f. para elmodelo de regresión binomial negativo es,
\[ \Pr ({Y_i} = {y_i}) = \frac{{\Gamma ({y_i} + v)}}{y_i{!}\Gamma (v)} \left( \frac{v}{v + {\mu _i}} \right)^v \left( \frac{\mu _i}{v + {\mu _i}} \right)^{y_i},{y_i} = 0,1,2,..., \]
donde la media es \(E({Y_i}) = {\mu _i}\), la varianza es \(Var({Y_i}) = {\mu _i}(1 + {v^{ - 1}}{\mu _i}) = {\mu _i}(1 + a{\mu _i})\), y \({v^{ - 1}} = a\) indica el parámetro de dispersión. El modelo de regresión BN se reduce al modelo de regresión de Poisson en el límite cuando \(a \to 0\), y produce sobredispersión cuando \(a > 0\). Se puede asumir también que la media sigue el enlace logarítmico, \(E({Y_i}) = {\mu _i} = \exp ({{\bf x}_{\bf i}{\bf{'\beta }}})\), y los estimadores máximo verosímiles pueden obtenerse maximizando la log verosimilitud.
12.5.3 Tarificación de Primas con datos Bonus-Malus
En esta sección, consideraremos la aproximación estadística de obtener tarifas usando los datos de conteo (datos de frecuencia) que proporciona la información bonus-malus sobre los perfiles de riesgo de los asegurados.
Ejemplo 10
Consideremos los datos sobre el seguro privado de responsabilidad de autos en Canadá obtenidos de Bailey y Simon (1960). Los datos proporcionan información sobre el número de siniestros producidos y la exposición (expresados en términos del número de años de antigüedad del vehículo). Los datos se clasifican dentro de dos grupos de factores de tarificación; mérito y clase. Todo ello supone veinte \((4 \times 5)\) clases de tarificación cruzadas de frecuencias de siniestros (20 datos de conteo). La Tabla 5 proporciona la descripción de los dos grupos de factores de tarificación. Puede verse que los factores de mérito proporcionan información sobre el número de años sin accidentes, y de este modo, la información puede usarse como información bonus-malus. Usando los datos del seguro de automóviles Canadiense:
Ajusta el modelo de regresión de Poisson usando los datos de conteo.
Calcula la prima asumiendo que la severidad por siniestro es 1000 para todos los grupos de tarificación.
Construye una tabla de primas simple, y sugiere el porcentaje de descuentos (o recargos) para las primas si se considera el BMS.
\[ \begin{matrix} \text{Tabla 5: Factores de Tarificación (datos de Canadá)}\\ \begin{array}{*{20}c} \hline \text{Mérito} & \text{Clase}\\ \hline\\ \text{A = con carnet, sin accidentes ≥ 3 años } & \text{1 = ningún conductor masculino < 25 } \\ \text{X = con carnet, sin accidentes 2 años } & \text{2 = conductor masculino ocasional < 25 } \\ \text{Y = con carnet, sin accidentes 1 año } & \text{3 = uso laboral} \\ \text{B = otros} & \text{4 = propietario no casado / conductor principal < 25} \\ & \text{5 = propietario casado / conductor principal < 25 } \\\\ \hline \end{array} \end{matrix} \]
Solución
La Tabla 6 proporciona los parámetros estimados (y los errores estándar) para el modelo de regresión de Poisson que es ajustado a los datos de conteo.
Las primas se calculan multiplicando las frecuencias ajustadas por las severidades de los siniestros. La frecuencia ajustada se calcula dividiendo los conteos ajustados entre la exposición. El conteo ajustado, \(E({Y_i}) = {\mu _i} = {\hat y_i}\), es el valor ajustado obtenido a partir del modelo de regresión de Poisson. Las primas para todas las clases de tarificación se muestran en la Tabla 7.
Sea la prima asignada al mérito B la prima base. Pueden calcularse los cambios en la prima y el porcentaje de descuentos para cada tarifa, como se muestra en los valores presentados en la Tabla 8. En la Tabla 9 presentamos una tabla de primas simple que proporciona el porcentaje de descuentos en función del número de años sin siniestros. Los descuentos pueden aplicarse por la aplicación del BMS.
\[ \begin{matrix} \text{Table 6: Modelo de regresión de Poisson (datos Canadienses)}\\ \begin{array}{*{20}c} \hline \text{Parámetro de la regresión} & \text{est.} & \text{error std.} & p\text{ -valor} \\ \hline\\ \text{constante} & {-2,53} & {0,00} & {0,00} \\ \text{Clase 2} & {0,30} & {0,01} & {0,00} \\ \text{Clase 3} & {0,47} & {0,01} & {0,00} \\ \text{Clase 4} & {0,53} & {0,01} & {0,00} \\ \text{Clase 5} & {0,22} & {0,01} & {0,00} \\ \text{Mérito X} & {0,27} & {0,01} & {0,00} \\ \text{Mérito Y} & {0,36} & {0,01} & {0,00} \\ \text{Mérito B} & {0,49} & {0,00} & {0,00} \\ & & & \\ \text{Log }L & {-394,96} & & \\\\ \hline \end{array} \end{matrix} \]
\[ \begin{matrix} \text{Tabla 7: Conteo ajustado, frecuencia ajustada y prima (datos Canadienses)}\\ \begin{array}{*{20}c} \hline \text{Clase} & \text{Mérito} & & & \text{Frecuencia Ajustada} & \text{Prima} \\ \text{tarifa} & \text{tarifa} & \text{Conteo ajustado} & \text{Exposición} & \text{(conteo/exposición)} & \text{(frecuencia x 1000)}\\ \hline\\ 1 & \text{A} & 219950 & 2757520 & 0,08 & 80 \\ 1 & \text{X} & 13688 & 130706 & 0,1 & 105 \\ 1 & \text{Y} & 18608 & 163544 & 0,11 & 114 \\ 1 & \text{B} & 35773 & 273944 & 0,13 & 131 \\ 2 & \text{A} & 14052 & 130535 & 0,11 & 108 \\ 2 & \text{X} & 1022 & 7233 & 0,14 & 141 \\ 2 & \text{Y} & 1494 & 9726 & 0,15 & 154 \\ 2 & \text{B} & 3790 & 21504 & 0,18 & 176 \\ 3 & \text{A} & 31547 & 247424 & 0,13 & 128 \\ 3 & \text{X} & 2656 & 15868 & 0,17 & 167 \\ 3 & \text{Y} & 3705 & 20369 & 0,18 & 182 \\ 3 & \text{B} & 7862 & 37666 & 0,21 & 209 \\ 4 & \text{A} & 21170 & 156871 & 0,13 & 135 \\ 4 & \text{X} & 3137 & 17707 & 0,18 & 177 \\ 4 & \text{Y} & 4060 & 21089 & 0,19 & 193 \\ 4 & \text{B} & 12534 & 56730 & 0,22 & 221 \\ 5 & \text{A} & 6346 & 64130 & 0,1 & 99 \\ 5 & \text{X} & 525 & 4039 & 0,13 & 130 \\ 5 & \text{Y} & 687 & 4869 & 0,14 & 141 \\ 5 & \text{B} & 1393 & 8601 & 0,16 & 162 \\\\ \hline \end{array} \end{matrix} \]
\[ \begin{matrix} \text{Tabla 8: Cambios en la prima (datos Canadienses)}\\ \begin{array}{*{20}c} \hline \text{Clase} & \text{Mérito} & \text{Prima} & \text{Cambio en la prima} & \text{Descuento} \\ \hline\\ 1 & \text{A} & 80 & 0,61 & 39 \\ & \text{X} & 105 & 0,80 & 20 \\ & \text{Y} & 114 & 0,87 & 13 \\ & \text{B} & 131 & 1,00 & 0 \\ 2 & \text{A} & 108 & 0,61 & 39 \\ & \text{X} & 141 & 0,80 & 20 \\ & \text{Y} & 154 & 0,88 & 13 \\ & \text{B} & 176 & 1,00 & 0 \\ 3 & \text{A} & 128 & 0,61 & 39 \\ & \text{X} & 167 & 0,80 & 20 \\ & \text{Y} & 182 & 0,87 & 13 \\ & \text{B} & 209 & 1,00 & 0 \\ 4 & \text{A} & 135 & 0,61 & 39 \\ & \text{X} & 177 & 0,80 & 20 \\ & \text{Y} & 193 & 0,87 & 13 \\ & \text{B} & 221 & 1,00 & 0 \\ 5 & \text{A} & 99 & 0,61 & 39 \\ & \text{X} & 130 & 0,80 & 20 \\ & \text{Y} & 141 & 0,87 & 13 \\ & \text{B} & 162 & 1,00 & 0 \\\\ \hline \end{array} \end{matrix}\]
\[ \begin{matrix} \text{Tabla 9: Tarifas y BMS (datos Canadienses)}\\ \begin{array}{*{20}c} \hline \text{Clase} & \text{Prima} & \text{Años} & \text{Descuento por} \\ & & \text{sin accidentes} & \text{bonus-malus }\\ \hline\\ 1 & 131 & {3+} & 39 \\ & & 2 & 20 \\ & & 1 & 13 \\ & & 0 & 0 \\ 2 & 176 & {3+} & 39 \\ & & 2 & 20 \\ & & 1 & 13 \\ & & 0 & 0 \\ 3 & 209 & {3+} & 39 \\ & & 2 & 20 \\ & & 1 & 13 \\ & & 0 & 0 \\ 4 & 221 & {3+} & 39 \\ & & 2 & 20 \\ & & 1 & 13 \\ & & 0 & 0 \\ 5 & 162 & {3+} & 39 \\ & & 2 & 20 \\ & & 1 & 13 \\ & & 0 & 0 \\\\ \hline \end{array} \end{matrix}\]
12.5.4 Tarificación sin datos Bonus-Malus
En esta sección nos centramos en el análisis estadístico de la obtención de tarifas usando datos de conteo que no proporcionan información bonus-malus sobre el perfil de riesgo de los asegurados.
Ejemplo 11
Utilizamos la base de datos sobre siniestros con daños a todo riesgo (OD) en el seguro de automóviles en Malasia (Zamani y Ismail 2012, Ismail y Zamani 2013). Los datos recogen información sobre 1,01 millones de pólizas de autos durante un periodo de tres años, 2001-2003. Las exposiciones se expresan en unidades coche-año.
La Tabla 10 muestra los factores de tarificación para los datos de conteo de siniestros. En total son \(5 \times 5 \times 5 \times 5 = 625\) clases de tarificación cruzadas de frecuencias de siniestros (625 datos de conteo).
Sin embargo, el número de clases de tarificación (tamaño muestral) se reduce a 547 después de excluir aquellos datos de conteo con exposición cero. A partir de la descripción presentada en la Tabla 10 observamos que los datos no proporcionan información sobre el número de años sin siniestros (información bonus-malus). Usando los datos del seguro de automóviles de Malasia:
Ajustar los datos de conteo usando los modelos de regresión de Poisson y binomial negativo. Comparar ambos modelos sugiriendo el modelo preferido para los datos.
Calcular la prima asumiendo que la severidad de los siniestros es de 1000 MYR (Ringgit Malaysia) para todas las tarifas o grupos de tarificación.
Construir la tabla de primas, asumiendo que se implementa el sistema NCD.
\[ \begin{matrix} \text{Tabla 10: Fatores de tarificación (datos de Malasia)}\\ \begin{array}{*{20}c} \hline \text{Factores de tarificación} & \text{Descripción} \\ \hline\\ \text{Edad del vehículo} & \text{0-1 años } \\ & \text{2-3 años} \\ & \text{4-5 años} \\ & \text{6-7 años} \\ & \text{8+ años} \\ \text{Vehículo c.c.} & \text{0-1000} \\ & \text{1001-1300} \\ & \text{1301-1500} \\ & \text{1501-1800} \\ & \text{1801+} \\ \text{Marca del vehículo} & \text{Local tipo 1} \\ & \text{Local tipo 2} \\ & \text{Extranjera tipo 1} \\ & \text{Extranjera tipo 2} \\ & \text{Extranjera tipo 3} \\ \text{Área geográfica} & \text{Norte} \\ & \text{Este} \\ & \text{Central} \\ & \text{Sur} \\ & \text{Malasia este} \\\\ \hline \end{array} \end{matrix} \]
Solución
La Tabla 11 muestra los parámetros estimados (y errores estándar) para los modelos de regresión Poisson y binomial negativo ajustados. Los resultados indican valores similares para los parámetros estimados. La ratio de verosimilitud en relación a la sobredispersión entre los modelos Poisson y BN es 2844,14, indicando que los datos están sobredispersos y que el BN es el mejor modelo. El AIC y el BIC también indican que el BN es el mejor modelo. La Tabla 12 muestra los parámetros estimados (y errores estándar) para el modelo de regresión binomial negativo con covariables significativas (se excluyen las covariables con \(p\)-valor mayor que 0,10). El modelo BN presentado en la Tabla 12 se selecciona como el modelo preferido para los datos.
Las primas se calculan multiplicando las frecuencias ajustadas por las severidades de los siniestros. Las primas para las primeras 25 clases de tarificación (edad del vehículo: 0-1 años y marca del vehículo: local-tipo 1) aparecen en la Tabla 13.
El sistema NCD malasio tiene seis clases de descuentos (0%, 25%, 30%,38,3%, 45% and 55%) para 0, 1, 2, 3, 4 y 5+ años sin siniestros. Las primas finales deben ser ‘infladas’ de acuerdo a lo que indica el NCD (derecho a descuento) de cada asegurado. Podemos usar la distribución estacionaria para aproximar la proporción de asegurados en cada clase NCD (en el largo plazo). Asumamos que la probabilidad de un año sin siniestros para todas las clases NCD es 0,90. Las probabilidades estacionarias son (a partir del Ejemplo 3):
\[ {\pi_0} = 0,1000,\rm{ }{\pi _1} = 0,0900,\rm{ }{\pi _2} = 0,0810,\rm{ }{\pi _3} = 0,0729,\rm{ }{\pi _4} = 0,0656,\rm{ }{\pi _5} = 0,5905 \]
que indica que el 10% de los asegurados finalmente pertenecen a la clase 0 (cero años sin siniestros), 9% de los asegurados finalmente pertenecen a la clase 1 (un año sin siniestros), y así sucesivamente, hasta el 59% de los asegurados finalmente incluidos en la clase 5 (cinco años sucesivos sin siniestros). Después de implementar el sistema NCD, la prima se reduce en media (en el largo plazo) de acuerdo al siguiente factor:
\[ \begin{array}{l} = \sum\limits_j \text{(proporción de asegurados en la clase}j)\text{(1 - NCD en la clase}j) \\\\ = (0,1000)(1) + (0,0900)(1 – 0,25) + ... + (0,5905)(1 – 0,55)\\\\ = {0}{,570962} \end{array} \]
Por tanto, las primas finales (después de ajustar por el NCD) deberían ser incrementadas por \(1 \div 0,57 = 1,75\). Podemos construir una tabla de primas teniendo en cuenta el factor (1,75). Las primas finales para las primeras 5 clases de tarificación aparecen en la Tabla 14, y pueden utilizarse para implementar el NCD.
\[ \begin{matrix} \text{Tabla 11: Modelos de regresión de Poisson y binomial negativo (datos de Malasia)}\\ \begin{array}{*{20}c} \hline \text{Parámetros} & \text{Poisson} & \text{Poisson} & \text{BN} & \text{BN} \\ & \text{Est.} & {p}\text{ -valor} & \text{Est.} & {p}\text{ -valor} \\ \hline\\ \text{Constante} & {-3,04} & {0,00} & -3,17 & 0,00 \\ \text{2-3 años} & {0,51} & {0,00} & 0,57 & 0,00 \\ \text{4-5 años } & {0,52} & {0,00} & 0,52 & 0,00 \\ \text{6-7 años } & {0,43} & {0,00} & 0,40 & 0,00 \\ \text{8+ años } & {0,24} & {0,00} & 0,28 & 0,00 \\ \text{1001-1300 cc} & {-0,31} & {0,00} & -0,14 & 0,00 \\ \text{1301-1500 cc} & {-0,16} & {0,00} & 0,08 & 0,16 \\ \text{1501-1800 cc} & {0,14} & {0,00} & 0,25 & 0,00 \\ \text{1801+ cc} & {0,12} & {0,00} & 0,34 & 0,00 \\ \text{Local tipo 2} & {-0,46} & {0,00} & -0,30 & 0,00 \\ \text{Extranjero tipo 1} & {-0,21} & {0,00} & -0,31 & 0,00 \\ \text{Extranjero tipo 2} & {0,18} & {0,00} & 0,31 & 0,00 \\ \text{Extranjero tipo 3} & {-0,02} & {0,43} & -0,16 & 0,04 \\ \text{Este} & {0,35} & {0,00} & 0,30 & 0,00 \\ \text{Central} & {0,32} & {0,00} & 0,31 & 0,00 \\ \text{Sur} & {0,26} & {0,00} & 0,36 & 0,00 \\ \text{Malasia Este} & {0,13} & {0,00} & 0,11 & 0,08 \\ {a} & {-} & {-} & 0,13 & 0,00 \\ & & & & \\ \text{Log Verosimilitud} & & {-3.613,39} & & -2191,32 \\ \text{AIC} & & {7.260,79} & & 4418,65 \\ \text{BIC} & & {7.333,96} & & 4496,13 \\\\ \hline \end{array} \end{matrix} \]
\[ \begin{matrix} \text{Tabla 12: Modelo de regresión binomial Negativo con covariantes significativas (datos de Malasia)}\\ \begin{array}{*{20}c} \hline \text{Parámetros} & \text{Est.} & p\text{ -valor}\\ \hline \\ \text{Constante} & {-3,14} & {0,00}\\ \text{2-3 años} & {0,58} & {0,00}\\ \text{4-5 años} & {0,53} & {0,00}\\ \text{6-7 años} & {0,41} & {0,00}\\ \text{8+ años} & {0,29} & {0,00}\\ \text{1001-1300 cc} & {-0,17} & {0,00}\\ \text{1501-1800 cc} & {0,23} & {0,00}\\ \text{1801+ cc} & {0,32} & {0,00}\\ \text{Local tipo 2} & {-0,32} & {0,00}\\ \text{Extranjero tipo 1} & {-0,31} & {0,00}\\ \text{Extranjero tipo 2} & {0,31} & {0,00}\\ \text{Extranjero tipo 3} & {-0,18} & {0,02}\\ \text{Este} & {0,30} & {0,00}\\ \text{Central} & {0,31} & {0,00}\\ \text{Sur} & {0,36} & {0,00}\\ \text{Malasia Este} & {0,11} & {0,08}\\ \alpha\,\text{(dispersión)} & {0,13} & {0,00}\\\\ \text{Log verosimilitud} & & {-2192,34}\\ \text{AIC} & & {4418,68}\\ \text{BIC} & & {4491,85}\\\\ \hline \end{array} \end{matrix} \]
\[ \begin{matrix} \text{Tabla 13: Primas (datos de Malasia)}\\ \begin{array}{*{20}c} \hline \text{Vehículo} & \text{Vehículo} & \text{Vehículo} & \text{área geogr.} & \text{exposición} & \text{Ajustado} & \text{Prima}\\ \text{año} & \text{cc} & \text{marca} & & & \text{conteo} & \left(\frac{ajustado\,conteo}{exposicion} \times 1000 \right)\\ \hline\\ 0-1\,\text{año} & {0-1000} & \text{local-1} & \text{norte} & {34} & {1} & {29}\\ & & & \text{este} & {11} & {1} & {91}\\ & & & \text{central} & {184} & {11} & {60}\\ & & & \text{sur} & {14} & {1} & {71}\\ & & & \text{Malasia este} & {22} & {1} & {45}\\ & & \text{local-2} & \text{norte} & {17881} & {562} & {31}\\ & & & \text{este} & {7581} & {322} & {42}\\ & & & \text{central} & {19699} & {844} & {43}\\ & & & \text{sur} & {8268} & {371} & {45}\\ & & & \text{Malasia este} & {12229} & {429} & {35}\\ & & \text{extranjero-1} & \text{norte} & {241} & {8} & {33}\\ & & & \text{este} & {44} & {2} & {45}\\ & & & \text{central} & {254} & {11} & {43}\\ & & & \text{sur} & {35} & {2} & {57}\\ & & & \text{Malasia este} & {113} & {4} & {35}\\ & & \text{extranjero-2} & \text{norte} & {64} & {4} & {63}\\ & & & \text{este} & {7} & {1} & {143}\\ & & & \text{central} & {164} & {13} & {79}\\ & & & \text{sur} & {23} & {2} & {87}\\ & & & \text{Malasia este} & {45} & {1} & {67}\\ & & \text{extranjero-3} & \text{norte} & {7512} & {274} & {36}\\ & & & \text{este} & {2747} & {135} & {49}\\ & & & \text{central} & {15551} & {774} & {50}\\ & & & \text{sur} & {7408} & {387} & {52}\\ & & & \text{Malasia este} & {6740} & {274} & {41}\\\\ \hline \end{array} \end{matrix} \]
\[ \begin{matrix} \text{Tabla 14: Prima, prima final y NCD (datos de Malasia)}\\ \begin{array}{*{20}c} \hline \text{Vehículo} & \text{Vehículo} & \text{Vehículo} & \text{área geogr.} & \text{Prima} & \text{Final} & \text{Años} & \text{NCD}\\ \text{año} & \text{cc} & \text{marca} & & & \text{Prima} & \text{sin siniestros} & \left( \% \right)\\ & & & & & \left( \text{prima} \times \text{1,75}\right) & & \\ \hline\\ 0-1\,\text{año} & {0-1000} & \text{local-1} & \text{norte} & {29} & {51} & {5+} & {55}\\ & & & & & & {4} & {45}\\ & & & & & & {3} & {38,33}\\ & & & & & & {2} & {30}\\ & & & & & & {1} & {25}\\ & & & & & & {0} & {0}\\ & & & \text{este} & {91} & {159} & {0} & {55}\\ & & & & & & {1} & {45}\\ & & & & & & {2} & {38,33}\\ & & & & & & {3} & {30}\\ & & & & & & {4} & {25}\\ & & & & & & {5+} & {0}\\ & & & \text{central} & {60} & {105} & {0} & {55}\\ & & & & & & {1} & {45}\\ & & & & & & {2} & {38,33}\\ & & & & & & {3} & {30}\\ & & & & & & {4} & {25}\\ & & & & & & {5+} & {0}\\ & & & \text{sur} & {71} & {125} & {0} & {55}\\ & & & & & & {1} & {45}\\ & & & & & & {2} & {38,33}\\ & & & & & & {3} & {30}\\ & & & & & & {4} & {25}\\ & & & & & & {5+} & {0}\\ & & & \text{Malasia este} & {45} & {80} & {0} & {55}\\ & & & & & & {1} & {45}\\ & & & & & & {2} & {38,33}\\ & & & & & & {3} & {30}\\ & & & & & & {4} & {25}\\ & & & & & & {5+} & {0}\\ \vdots & \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots\\\\ \hline \end{array} \end{matrix} \]
Colaboradores
- Traducción al español: Mercedes Ayuso (Universitat de Barcelona)
LECTURAS ADICIONALES Y REFERENCIAS:
Aitkin, M., Anderson, D., Francis, B., Hinde, J. 1990. Statistical Modelling in GLIM. New York: Oxford University Press.
Ajne, B. 1975. A note on the multiplicative ratemaking model. ASTIN Bulletin 8(2): 144-153.
Anderson, D., Feldblum, S., Modlin, C., Schirmacher, D., Schirmacher, E., Thandi, N. 2004. A practitioner's guide to Generalized Linear Models. Casualty Actuarial Society Discussion Paper Program 1-115.
Bailey, R.A. 1963. Insurance rates with minimum bias. Proceedings of the Casualty Actuarial Society 50(93): 4-14.
Bailey, R.A., Simon, L.J. 1960. Two studies in automobile insurance ratemaking. ASTIN Bulletin 49(1): 192-217.
Bichsel, F. 1964. Erfahrungs-Tarifierung in der Motorfahrzeug-halfplichtversicherung. Milleilungen der Vereinigung Schweizerischer Versicherungsmathematiker 119-129.
Boucher, J.P., Denuit, M., Guillen, M. 2007. Risk classification for claim count: a comparative analysis of various zero-inflated mixed Poisson and hurdle models. North American Actuarial Journal 11(4): 110-131.
Brockmann, M.J., Wright, T.S. 1992. Statistical motor rating: making effective use of your data. Journal of the Institute of Actuaries 119(3): 457-543.
Brown, R.L. 1988. Minimum bias with generalized linear models. Proceedings of the Casualty Actuarial Society 75(143): 187-217.
Bühlmann, H. 1964. Optimale Prämienstufen systeme. Milleilungen der Vereinigung Schweizerischer Versicherungsmathematiker 193-213.
Cameron, A.C., Trivedi, P.K. 1986. Econometric models based on count data: comparisons and applications of some estimators and tests. Journal of Applied Econometrics 1: 29-53.
Cameron, A.C., Trivedi, P.K. 1998. Regression Analysis of Count Data. New York: Cambridge University Press.
Chamberlain, C. 1980. Relativity pricing through analysis of variance. Casualty Actuarial Society Discussion Paper Program 4-24.
Corlier, F., Lemaire, J., & Muhokolo, D. (1979). Simulation of an automobile portfolio. The Geneva Papers on Risk and Insurance Theory 4:40-46.
Coutts, S.M. 1984. Motor insurance rating, an actuarial approach. Journal of the Institute of Actuaries 111: 87-148.
Delaporte, P. 1965. Tarification du risque individuel d’accidents par la prime modelil ée sur le risqué. ASTIN Bulletin 3: 251-271.
Denuit, M., Marechal, X., Pitrebois, S., Walhin, J.F. 2007. Actuarial Modeling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. John Wiley and Sons: England.
Dionne, G., & Vanasse, C. (1989). A generalization of automobile insurance rating models: the negative binomial distribution with a regression component. ASTIN Bullettin 19(2): 199-212.
Frangos, N. E., Vrontos, S. D. 2001. Design of optimal bonus-malus systems with a frequency and severity component on an individual basis in automobile insurance. ASTIN Bulletin 31(1): 1-22.
Harrington, S.E. 1986. Estimation and testing for functional form in pure premium regression models. ASTIN Bulletin 16: 31-43.
Hastings, N.A.J. 1976. Optimal claiming on vehicle insurance. Operational Research Quarterly 27: 805-813.
Hilbe, J. 2007. Negative Binomial Regression. Cambridge, UK: Cambridge University Press.
Ismail, N., Jemain, A.A. 2005. Bridging minimum bias and maximum likelihood methods through weighted equation. Casualty Actuarial Society Forum Spring: 367-394.
Ismail, N., Jemain, A.A. 2007. Handling overdispersion with negative binomial and generalized Poisson regression models. Casualty Actuarial Society Forum Winter: 103-158.
Ismail, N., Zamani, H. 2013. Estimation of claim count data using negative binomial, generalized Poisson, zero-inflated negative binomial and zero-inflated generalized Poisson regression models. Casualty Actuarial Society E-Forum Spring: 1-29.
Jung, J. 1968. On automobile insurance ratemaking. ASTIN Bulletin 5(1): 41-48.
Kolderman, J., Volgenant, A. 1985. Optimal claiming in an automobile insurance system with bonus-malus structure. Journal of the Operational Research Society 36: 239-247.
Lawless, J.F. 1987. Negative binomial and mixed Poisson regression. Canadian Journal of Statistics 15(3): 209-225.
Lemaire, J. 1976. Driver versus company, optimal behaviour of the policy holder. Scandinavian Actuarial Journal 59: 209-219.
Lemaire, J. 1977. La soif du bonus. ASTIN Bulletin 9: 181-190.
Lemaire, J. 1979. How to define a Bonus-Malus system with an exponential utility function. ASTIN Bulletin 10: 274-282.
Lemaire, J., Zi, H.M. 1994. A comparative analysis of 30 Bonus-Malus systems. ASTIN Bulletin 24: 287-309.
Lemaire, J. 1998. Bonus-Malus systems: The European and Asian approach to merit-rating. North American Actuarial Journal 2(1): 26-38.
Loimaranta, K. 1972. Some asymptotic properties of bonus systems. ASTIN Bulletin 6: 233-245.
McCullagh, P., Nelder, J.A. 1989. Generalized Linear Models (2nd Edition). Chapman and Hall: London.
Morillo, I., Bermúdez, L. 2003. Bonus–malus system using an exponential loss function with an inverse Gaussian distribution. Insurance: Mathematics and Economics 33: 49-57.
Pitrebois, S., Denuit, M., Walhin, J.F. 2003. Fitting the Belgian Bonus-Malus system. Belgian Actuarial Bulletin 3(1): 58-62.
Renshaw, A.E., 1994. Modelling the claims process in the presence of covariates. ASTIN Bulletin 24(2): 265-285.
Tremblay, L. 1992. Using the Poisson inverse Gaussian in Bonus-Malus systems. ASTIN Bulletin 22(1): 97-106.
Vepsäläinen, S. 1972. Applications to a theory of bonus systems. ASTIN Bulletin 6: 212-221.
Walhin, J. F., Paris, J. 1999. Using mixed Poisson processes in connection with Bonus-Malus systems. ASTIN Bulletin 29(1): 81-99.
Winkelmann, R. 2008. Econometric Analysis of Count Data. Heidelberg: Springer Verlag.
Zamani, H., Ismail, N. 2012. Functional form for the generalized Poisson regression model. Communications in Statistics (Theory and Methods) 41(20): 3666–3675.