Chapter 6 Simulación y Remuestreo

Vista previa del capítulo. La simulación es un método computacionalmente intenso usado para resolver problemas difíciles. En lugar de crear procesos físicos y experimentar con ellos para entender sus características operacionales, un estudio de simulación se basa en una representación computacional – considera varias condiciones hipotéticas como inputs y resume los resultados. Aunque se trata de una simulación, un gran número de condiciones hipotéticas pueden ser rápidamente examinadas con un bajo coste. La sección 6.1 introduce la simulación, una herramienta computacional maravillosa que es especialmente útil en entornos complejos multivariantes.

También podemos usar la simulación para realizar extracciones de una distribución empírica – proceso que se llama remuestreo. El remuestreo permite valorar la incertidumbre de las estimaciones en modelos complejos. La sección 6.2 introduce el remuestreo en el contexto del bootstrapping para determinar la precisión de los estimadores.

Las secciones siguientes introducen otros temas del remuestreo. La Sección 6.3 sobre la validación cruzada muestra como usarla para la selección y validación de modelos. La sección 6.4 sobre la importancia del muestreo describe el remuestreo en áreas específicas de interés, como en aplicaciones actuariales con colas largas. La sección 6.5 sobre el método de Monte Carlo basado en cadenas de Markov (MCMC, en sus siglas en inglés) introduce la simulación y el motor del remuestreo que apunta en buena medida el análisis Bayesiano moderno.

6.1 Fundamentos de la Simulación

En esta sección, se muestra como:

  • Generar realizaciones aproximadamente independientes distribuidas uniformemente
  • Transformar las realizaciones distribuidas uniformemente en observaciones de la distribución de probabilidad de interés
  • Calcular cantidades de interés y determinar la precisión de las cantidades calculadas

6.1.1 Generación de observaciones uniformes independientes

Las simulaciones que consideramos son generadas por ordenadores. La principal ventaja de este enfoque es que pueden ser replicadas, permitiéndonos realizar comprobaciones y mejorar nuestro trabajo. Naturalmente, esto también significa que no son realmente aleatorias. Sin embargo, se han desarrollado algoritmos para que los resultados se comporten como aleatorios a efectos prácticos. En concreto, pasan test de independencia sofisticados y pueden ser diseñados de modo que provengan de una única distribución – nuestro supuesto iid, idénticamente e independientemente distribuidas, según sus siglas en inglés.

Para tener una idea de lo que estos algoritmos hacen, consideramos un método de importancia histórica.

Generador Lineal Congruencial. Para generar una secuencia de números aleatorios, comenzamos con \(B_0\), un valor inicial que es conocido como semilla. Este valor se actualiza utilizando la relación recursiva \[B_{n+1} = a B_n + c \text{ modulo }m, ~~ n=0, 1, 2, \ldots .\] Este algoritmo se denomina generador lineal congruencial . El caso \(c=0\) se denomina generador congruencial multiplicativo; es particularmente útil para cálculos realmente rápidos.

Como valores ilustrativos de \(a\) y \(m\), Microsoft’s Visual Basic usa \(m=2^{24}\), \(a=1,140,671,485\), y \(c = 12,820,163\) (ver https://en.wikipedia.org/wiki/Linear_congruential_generator). Este es el generador subyacente en la generación de números aleatorios en el programa Microsoft Excel.

La secuencia usada por el analista se define como \(U_n=B_n/m.\) El analista puede interpretar la secuencia {\(U_{i}\)} como (aproximadamente) idénticamente e independientemente uniformemente distribuida en el intervalo (0,1). Para ilustrar el algoritmo, se considera lo siguiente.

Ejemplo 6.1.1. Secuencia ilustrativa.

Se asume \(m=15\), \(a=3\), \(c=2\) y \(B_0=1\). Entonces se tiene:

paso \(n\) \(B_n\) \(U_n\)
0 \(B_0=1\)
1 \(B_1 =\mod(3 \times 1 +2) = 5\) \(U_1 = \frac{5}{15}\)
2 \(B_2 =\mod(3 \times 5 +2) = 2\) \(U_2 = \frac{2}{15}\)
3 \(B_3 =\mod(3 \times 2 +2) = 8\) \(U_3 = \frac{8}{15}\)
4 \(B_4 =\mod(3 \times 8 +2) = 11\) \(U_4 = \frac{11}{15}\)

A veces, a los resultados aleatorios generados por ordenadores se les conoce como números pseudo-aleatorios, para reflejar el hecho de que son generados por una máquina y pueden ser replicados. Es decir, a pesar de que {\(U_{i}\)} parece ser i.i.d, puede ser reproducido usando el mismo valor de semilla (y el mismo algoritmo).

Ejemplo 6.1.2. Generación de números aleatorios uniformes en R.

El siguiente código muestra como generar tres números uniformes (0,1) en R usando el comando runif. La función set.seed() establece el valor inicial de la semilla. En muchos paquetes informáticos, la semilla inicial se establece usando el reloj del sistema, si no se especifica otra cosa.

Tres variables aleatorias uniformes
set.seed(2017)
U <- runif(3)
knitr::kable(U, digits=5, align = "c", col.names = "Uniforme")
Uniforme
0.92424
0.53718
0.46920

El generador lineal congruencial es simplemente un método para generar valores pseudo-aleatorios. Es fácil entender y es (todavía) ampliamente usado. El generador lineal congruencial tiene limitaciones, incluyendo el hecho de que es posible detectar patrones a largo plazo en el tiempo en las secuencias que genera (es necesario recordar que se puede interpretar independencia como una falta total de patrón funcional). No sorprende que se hayan desarrollado técnicas avanzadas para hacer frente a algunos de estos inconvenientes.

6.1.2 Método de la transformada inversa

Se parte de una secuencia de números aleatorios uniformes, y a continuación se transforma en la distribución de interés, sea \(F\). Una técnica destacada es el método de la transformada inversa, definido como

\[ X_i=F^{-1}\left( U_i \right) . \] Aquí, se recuerda que en la Sección 4.1.1 se ha introducido la función de distribución inversa, \(F^{-1}\), también referenciada como función cuantil. En concreto, se define como

\[ F^{-1}(y) = \inf_x ~ \{ F(x) \ge y \} . \] Se recuerda que \(\inf\) representa ínfimo o el máxima cota inferior. Es en esencia el valor más pequeño de x que satisface la desigualdad \(\{F(x) \ge y\}\). El resultado es que la secuencia {\(X_{i}\)} es aproximadamente iid con función de distribución \(F\).

El resultado de la transformada inversa puede obtenerse cuando la variable aleatoria es continua, discreta o una combinación híbrida de ambas. Ahora se presenta una serie de ejemplos para ilustrar el alcance de sus aplicaciones.

Ejemplo 6.1.3. Generar valores aleatorios exponenciales.

Se desea generar observaciones según una distribución exponencial con parámetro de escala \(\theta\) de manera que \(F(x) = 1 - e^{-x/\theta}\). Para calcular la transformada inversa, se siguen los siguientes pasos:

\[ \begin{aligned} y = F(x) &\iff y = 1-e^{-x/\theta} \\ &\iff-\theta \ln(1-y) = x = F^{-1}(y) . \end{aligned} \] Por tanto, si \(U\) tiene una distribución uniforme (0,1), entonces \(X = -\theta \ln(1-U)\) tiene una distribución exponencial con parámetro \(\theta\).

El siguiente código de R muestra como se puede comenzar con los mismos tres números aleatorios uniformes del Ejemplo 6.1.2 y transformarlos en variables aleatorias exponenciales independientes con media 10. Alternativamente, se puede usar directamente la función rexp de R para generar valores aleatorios según una distribución exponencial. El algoritmo que se construye en esta rutina es diferente por eso incluso con el mismo valor inicial de semilla, las realizaciones individuales pueden ser diferentes.

set.seed(2017)
U <- runif(3)
X1 <- -10*log(1-U)
set.seed(2017)
X2 <- rexp(3, rate = 1/10)
Tres variables aleatorias uniformes
Uniforme Exponencial 1 Exponencial 2
0.92424 25.80219 3.25222
0.53718 7.70409 8.47652
0.46920 6.33362 5.40176

Ejemplo 6.1.4. Generar valores aleatorios Pareto.

Se desea generar observaciones según una distribución de Pareto con parámetros \(\alpha\) y \(\theta\) de modo que \(F(x) = 1 - \left(\frac{\theta}{x+\theta} \right)^{\alpha}\). Para calcular la transformada inversa, se pueden seguir los siguientes pasos:

\[ \begin{aligned} y = F(x) &\Leftrightarrow 1-y = \left(\frac{\theta}{x+\theta} \right)^{\alpha} \\ &\Leftrightarrow \left(1-y\right)^{-1/\alpha} = \frac{x+\theta}{\theta} = \frac{x}{\theta} +1 \\ &\Leftrightarrow \theta \left((1-y)^{-1/\alpha} - 1\right) = x = F^{-1}(y) .\end{aligned} \]

Por tanto, \(X = \theta \left((1-U)^{-1/\alpha} - 1\right)\) tiene una distribución de Pareto con parámetros \(\alpha\) y \(\theta\).

Justificación de la transformada inversa. ¿Por qué la variable aleatoria \(X = F^{-1}(U)\) tiene función de distribución \(F\)?
Mostrar un fragmento de teoría

Ahora se consideran algunos ejemplos discretos.

Ejemplo 6.1.5. Generar valores aleatorios Bernoulli.

Se desea simular variables aleatorias que siguen una distribución Bernoulli con parámetro \(p=0.85\).

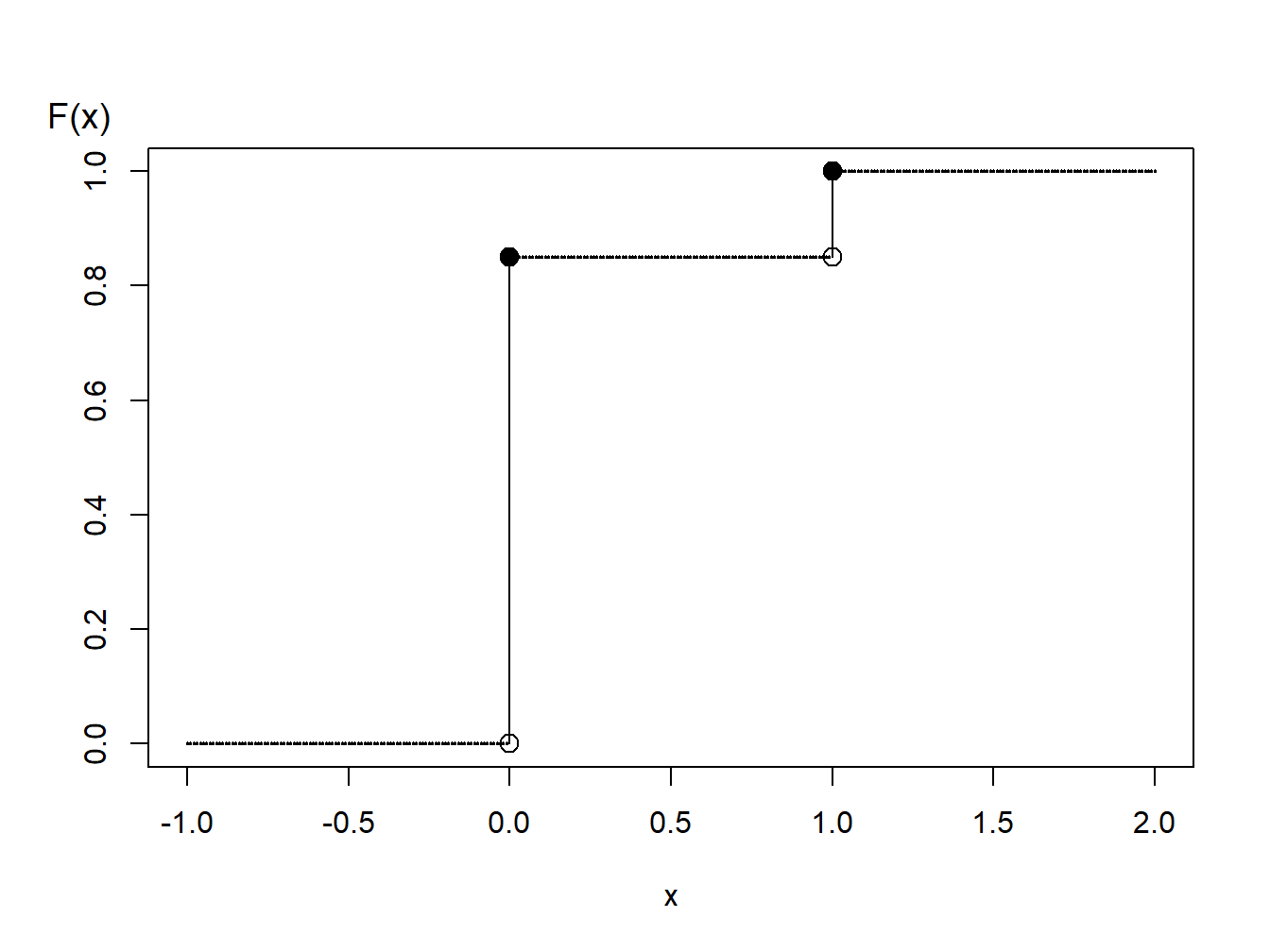
Función de distribución de una variable aleatoria binaria

Figure 6.1: Función de distribución de una variable aleatoria binaria

El gráfico de la función de distribución de la Figura 6.1 muestra que la función cuantil puede expresarse como

\[ \begin{aligned} F^{-1}(y) = \left\{ \begin{array}{cc} 0 & 0<y \leq 0.85 \\ 1 & 0.85 < y \leq 1.0 . \end{array} \right. \end{aligned} \] Por tanto, con la transformada inversa se puede definir

\[ \begin{aligned} X = \left\{ \begin{array}{cc} 0 & 0<U \leq 0.85 \\ 1 & 0.85 < U \leq 1.0 \end{array} \right. \end{aligned} \] A modo ilustrativo, se generan tres números aleatorios para obtener

set.seed(2017)
U <- runif(3)
X <- 1*(U > 0.85)

Tres variables aleatorias

Uniforme Binaria X
0.92424 1
0.53718 0
0.46920 0

Ejemplo 6.1.6. Generación de valores aleatorios de una distribución discreta.

Se considera el tiempo hasta que tiene lugar el fallo de una máquina en los primeros cinco años. La distribución de los tiempos de fallo viene dada por:

Distribución discreta
\(~~~~~~~~~~\) \(~~~~~~~~~~\) \(~~~~~~~~~~\) \(~~~~~~~~~~\) \(~~~~~~~~~~\)
Tiempo 1.0 2.0 3.0 4.0 5.0
Probabilidad 0.1 0.2 0.1 0.4 0.2
Función de distribución \(F(x)\) 0.1 0.3 0.4 0.8 1.0
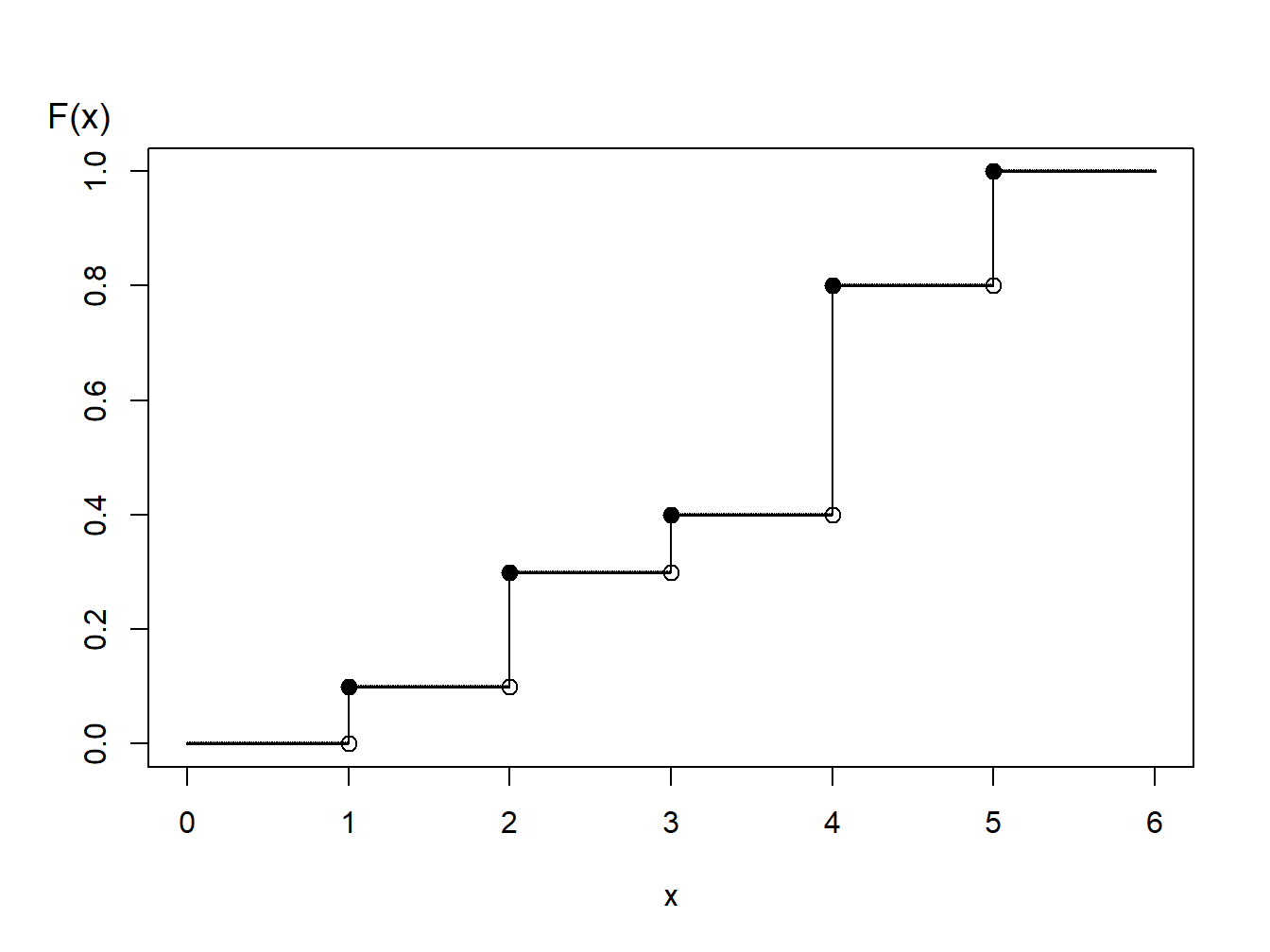
Función de Distribución de una Variable Aleatoria Discreta

Figure 6.2: Función de Distribución de una Variable Aleatoria Discreta

Usando el gráfico de la función de distribución en la Figura 6.2, con la transformada inversa se define

\[ \small{ \begin{aligned} X = \left\{ \begin{array}{cc} 1 & 0<U \leq 0.1 \\ 2 & 0.1 < U \leq 0.3\\ 3 & 0.3 < U \leq 0.4\\ 4 & 0.4 < U \leq 0.8 \\ 5 & 0.8 < U \leq 1.0 . \end{array} \right. \end{aligned} } \]

Para variables aleatorias discretas en general puede no existir una ordenación de valores. Por ejemplo, una persona puede tener uno de los cinco posibles tipos de seguros de vida y en ese caso el siguiente algoritmo se puede usar para generar valores aleatorios:

\[ {\small \begin{aligned} X = \left\{ \begin{array}{cc} \textrm{whole life} & 0<U \leq 0.1 \\ \textrm{endowment} & 0.1 < U \leq 0.3\\ \textrm{term life} & 0.3 < U \leq 0.4\\ \textrm{universal life} & 0.4 < U \leq 0.8 \\ \textrm{variable life} & 0.8 < U \leq 1.0 . \end{array} \right. \end{aligned} } \]

Otro analista puede usar un procedimiento alternativo como este:

\[ {\small \begin{aligned} X = \left\{ \begin{array}{cc} \textrm{whole life} & 0.9<U<1.0 \\ \textrm{endowment} & 0.7 \leq U < 0.9\\ \textrm{term life} & 0.6 \leq U < 0.7\\ \textrm{universal life} & 0.2 \leq U < 0.6 \\ \textrm{variable life} & 0 \leq U < 0.2 . \end{array} \right. \end{aligned} } \]

Ambos algoritmos producen (a largo plazo) las mismas probabilidades, e.g., \(\Pr(\textrm{whole life})=0.1\), etcétera. Por eso, ninguno es incorrecto. Es necesario tener en cuenta que hay muchos caminos para llegar a un mismo resultado. De manera similar, se podría emplear un algoritmo alternativo para valores ordenados (como los tiempos de fallo 1, 2, 3, 4, o 5, o más).

Ejemplo 6.1.7. Generar valores aleatorios de una distribución híbrida.

Se considera una variable aleatoria que es 0 con probabilidad 70% y tiene distribución exponencial con parámetro \(\theta= 10,000\) con probabilidad 30%. En una aplicación actuarial, esto podría corresponder a un 70% de probabilidad de no tener un siniestro y un 30% de probabilidades de tenerlo – si un siniestro ocurre, tiene una distribución exponencial. La función de distribución, representada en la Figura 6.3, viene dada por

\[ \begin{aligned} F(y) = \left\{ \begin{array}{cc} 0 & x<0 \\ 1 - 0.3 \exp(-x/10000) & x \ge 0 . \end{array} \right. \end{aligned} \]

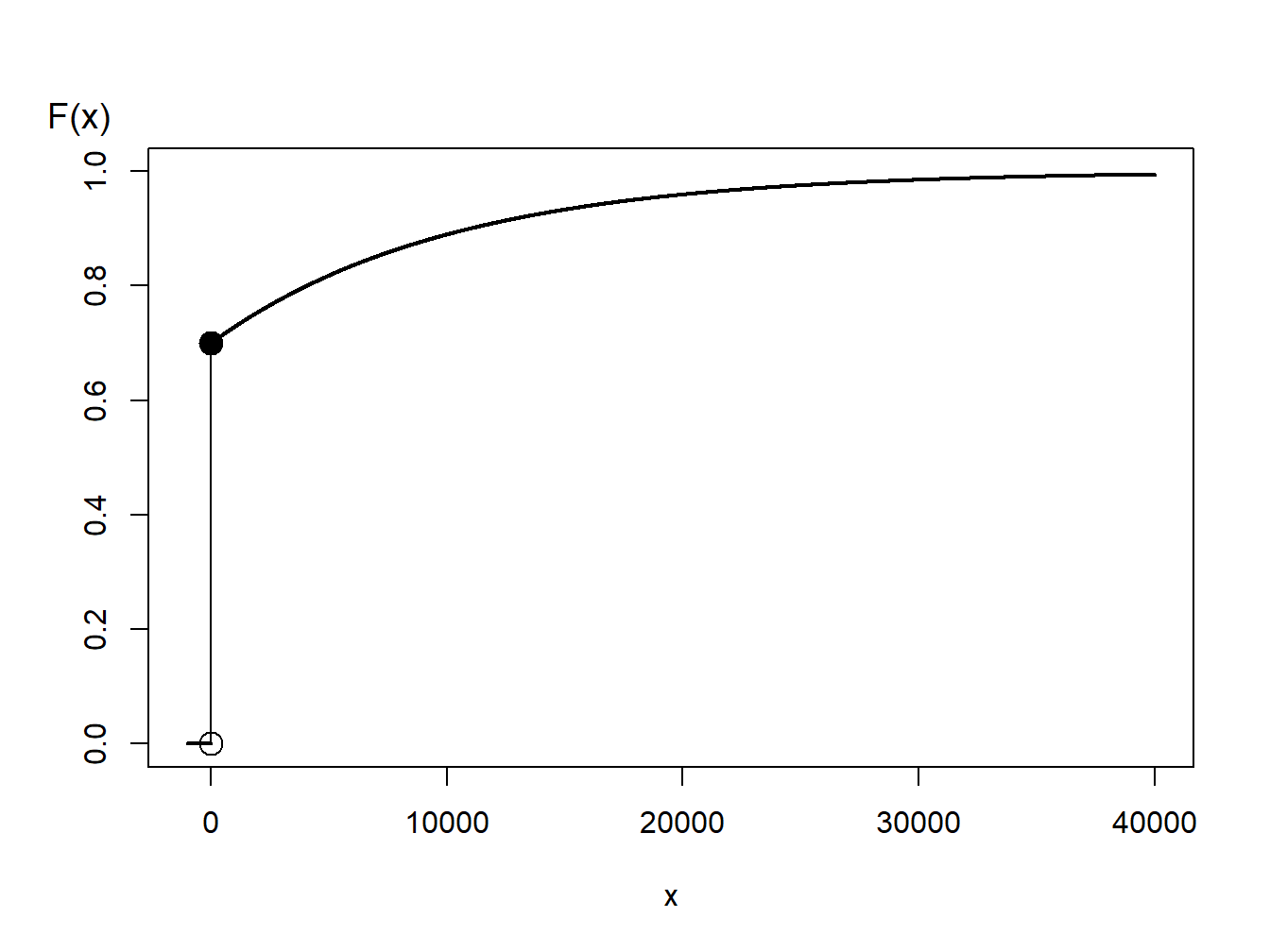
Función de distribución de una variable aleatoria híbrida

Figure 6.3: Función de distribución de una variable aleatoria híbrida

En la Figura 6.3, se puede ver que la transformada inversa para generar variables aleatorias con esta función de distribución es

\[ \begin{aligned} X = F^{-1}(U) = \left\{ \begin{array}{cc} 0 & 0< U \leq 0.7 \\ -1000 \ln (\frac{1-U}{0.3}) & 0.7 < U < 1 . \end{array} \right. \end{aligned} \] Para variables aleatorias discretas e híbridas, la clave es dibujar el gráfico de la función de distribución que permita visualizar valores potenciales de la función inversa.

6.1.3 Precisión de la simulación

De las subsecciones anteriores, se sabe cómo simular valores independientes de una distribución de interés. Con estas realizaciones, se puede construir una distribución empírica y aproximar la distribución subyacente con la precisión necesaria. A medida que se introduzcan más aplicaciones actuariales en este libro, se verá que la simulación puede ser aplicada en una gran variedad de contextos.

Muchas de estas aplicaciones pueden reducirse a un problema de aproximar \(\mathrm{E~}h(X)\), donde \(h(\cdot)\) es una función conocida. En base a \(R\) simulaciones (réplicas), se obtiene \(X_1,\ldots,X_R\). A partir de esta muestra simulada, se puede calcular la media

\[ \overline{h}_R=\frac{1}{R}\sum_{i=1}^{R} h(X_i) \] que se usa como la aproximación simulada (estimación) de \(\mathrm{E~}h(X)\). Para estimar la precisión de esta aproximación se usa la varianza de la simulación

\[ s_{h,R}^2 = \frac{1}{R-1} \sum_{i=1}^{R}\left( h(X_i) -\overline{h}_R \right) ^2. \] A partir del supuesto de independencia, el error estándar de la estimación es \(s_{h,R}/\sqrt{R}\). Esto se puede hacer tan pequeño como se desee incrementando el número de réplicas \(R\).

Ejemplo. 6.1.8. Gestión de carteras.

En la Sección 3.4, se explicó como calcular el valor esperado de pólizas con franquicias. Como ejemplo de algo que no puede hacerse con expresiones cerradas, se consideran ahora dos riesgos. Esta es una variación de un ejemplo más complejo que será presentado como Ejemplo 10.3.6.

Se consideran dos riesgos patrimoniales de una empresa de telecomunicaciones:

  • \(X_1\) - edificios, modelizado usando una distribución gamma con media 200 y parámetro de escala 100.
  • \(X_2\) - vehículos de motor, modelizado con una distribución gamma con media 400 y parámetro de escala 200.

El riesgo total se denota como \(X = X_1 + X_2.\) Por simplicidad, se asume que los riesgos son independientes.

Para gestionar el riesgo, se busca la protección de un seguro. Se desea gestionar internamente cuantías pequeñas asociadas a edificios y vehículos de motor, hasta \(M\). El riesgo retenido es \(Y_{retenido}=\) \(\min(X_1 + X_2,M)\). La porción del asegurador es \(Y_{asegurador} = X- Y_{retenido}\).

Para ser más concretos, se usa \(M=\) 400 así como \(R=\) 1000000 simulaciones.

a. Con las especificaciones, se desea determinar la cuantía esperada de siniestros y la desviación estándar asociada de (i) lo retenido, (ii) lo aceptado por el asegurador, y (iii) la cuantía total.

Se muestra el código R para la definición de los riesgos

Aquí está el código para las cuantías de siniestros esperadas.

Se muestra el código R para calcular las cuantías

Los resultados de estos cálculos son:

round(outMat,digits=2)
                    Retenido Asegurador  Total
Media                 365.17     235.01 600.18
Desviación estándar    69.51     280.86 316.36

b. Para siniestros asegurados, la aproximación del error estandar de la simulación es \(s_{h,R}/\sqrt{1000000} =\) 280.86 \(/\sqrt{1000000} =\) 0.281. Para este ejemplo, la simulación es rápida y un valor grande como 1000000 es una elección fácil. En cualquier caso, para problemas complejos, el tamaño de la simulación puede ser un problema.

Se muestra el código R para establecer la visualización

La Figura 6.4 permite visualizar el desarrollo de la aproximación a medida que aumenta el número de simulaciones.

matplot(1:R,sumP2[,1:20],type="l",col=rgb(1,0,0,.2), ylim=c(100, 400),
        xlab=expression(paste("Número de simulaciones (", italic('R'), ")")), ylab="Siniestros esperados por el asegurador")
abline(h=mean(Yinsurer),lty=2)
bonds <- cbind(1.96*sd(Yinsurer)*sqrt(1/(1:R)),-1.96*sd(Yinsurer)*sqrt(1/(1:R)))
matlines(1:R,bonds+mean(Yinsurer),col="red",lty=1)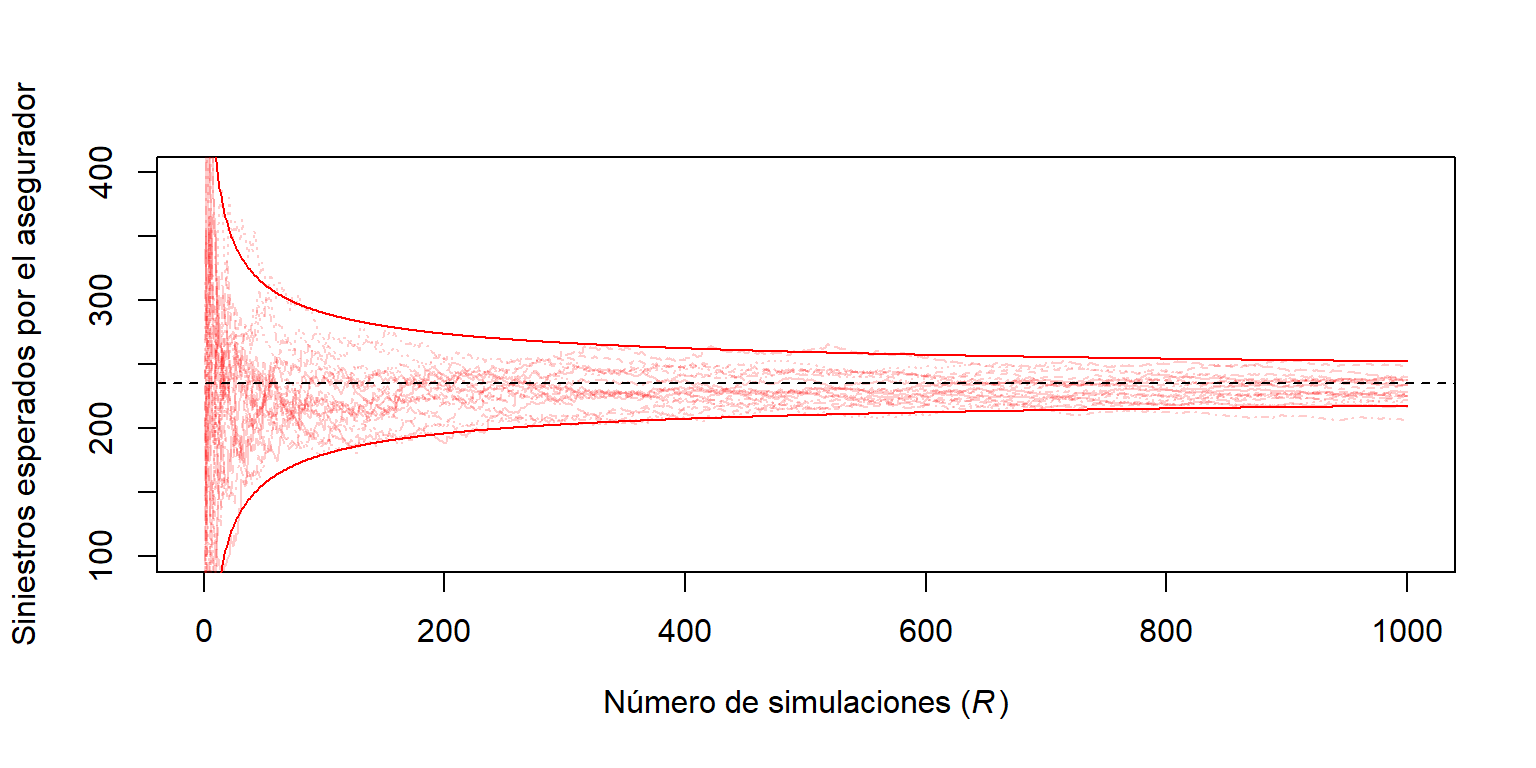
Estimación del número de siniestros esperados por el asegurador versus número de simulaciones.

Figure 6.4: Estimación del número de siniestros esperados por el asegurador versus número de simulaciones.

Determinación del número de simulaciones

¿Cuántos valores simulados se recomiendan? ¿100? ¿1,000,000? Se puede usar el teorema central del límite para responder a esta cuestión.

Como criterio para la confianza en el resultado, se supone que se desea estar dentro del 1% de la media con 95% de certeza. Es decir, se desea \(\Pr \left( |\overline{h}_R - \mathrm{E~}h(X)| \le 0.01 \mathrm{E~}h(X) \right) \le 0.95\). De acuerdo con el teorema central del límite, la estimación debe tener distribución aproximadamente normal, por lo que se desea que \(R\) sea suficientemente grande para satisfacer \(0.01 \mathrm{E~}h(X)/\sqrt{\mathrm{Var~}h(X)/R}) \ge 1.96\). (Se recuerda que 1.96 es el percentil 97.5 de una distribución normal estándar.) Reemplazando \(\mathrm{E~}h(X)\) y \(\mathrm{Var~}h(X)\) con sus estimaciones, se continúa la simulación hasta

\[ \frac{.01\overline{h}_R}{s_{h,R}/\sqrt{R}}\geq 1.96 \] o equivalentemente

\[\begin{equation} R \geq 38,416\frac{s_{h,R}^2}{\overline{h}_R^2}. \tag{6.1} \end{equation}\]

Este criterio es una aplicación directa de la aproximación a la normal. Nótese que \(\overline{h}_R\) y \(s_{h,R}\) no son conocidos de antemano, por lo que se tendrán que hacer estimaciones, bien haciendo un pequeño estudio piloto de antemano o interrumpiendo el procedimiento intermitentemente para ver si el criterio se satisface.

Ejemplo. 6.1.8. Gestión de carteras - continuación

En este ejemplo, el número medio de siniestros es 235.011 y la correspondiente desviación estándar es 280.862. Usando la ecuación (6.1), para estar dentro del 10% de la media, se requerirán al menos 54.87 miles de simulaciones. Sin embargo, para estar dentro del 1% se necesitarán al menos 5.49 millones de simulaciones.

Ejemplo. 6.1.9. Elección de la aproximación.

Una importante aplicación de la simulación es la aproximación de \(\mathrm{E~}h(X)\). En este ejemplo, se muestra que la elección de la función \(h(\cdot)\) y de la distribución de \(X\) pueden jugar un papel importante.

Se considera la siguiente pregunta: ¿cuál es \(\Pr[X>2]\) cuando \(X\) tiene una distribución de Cauchy, con densidad \(f(x) =\left(\pi(1+x^2)\right)^{-1}\), en la recta real? El valor real es

\[ \Pr\left[X>2\right] = \int_2^\infty \frac{dx}{\pi(1+x^2)} . \] Se puede usar una función de integración numérica en R (que funciona normalmente bien con integrales impropias)

true_value <- integrate(function(x) 1/(pi*(1+x^2)),lower=2,upper=Inf)$value

que es igual a 0.14758.

Alternativamente, se pueden usar técnicas de simulación para aproximar la cantidad. Usando el cálculo, se puede comprobar que la función cuantil de una distribución de Cauchy es \(F^{-1}(y) = \tan \left( \pi(y-0.5) \right)\). Entonces, con variables uniformes (0,1) simuladas, \(U_1, \ldots, U_R\), se puede construir el estimador

\[ p_1 = \frac{1}{R}\sum_{i=1}^R \mathrm{I}(F^{-1}(U_i)>2) = \frac{1}{R}\sum_{i=1}^R \mathrm{I}(\tan \left( \pi(U_i-0.5) \right)>2) . \]

Se muestra el código R

Con un millón de simulaciones, se obtiene una estimación de 0.14744 con error estándar 0.355 (dividido por 1000). Se puede demostrar que la varianza de \(p_1\) es de orden \(0.127/R\).

Con otras elecciones de \(h(\cdot)\) y \(F(\cdot)\), es en realidad posible reducir la incertidumbre incluso usando el mismo número de simulaciones en R. Para empezar, se puede usar la simetría de la distribución de Cauchy para determinar que \(\Pr[X>2]=0.5\cdot\Pr[|X|>2]\). Con ello, se puede construir un nuevo estimador

\[ p_2 = \frac{1}{2R}\sum_{i=1}^R \mathrm{I}(|F^{-1}(U_i)|>2) . \]

Con un millón de simulaciones, se obtiene una estimación de 0.14748 con error estándar 0.228 (dividido por 1000). Se puede demostrar que la varianza de \(p_2\) es de orden \(0.052/R\).

<!—Esto puede visualizarse abajo –>

Pero se puede ir un paso más adelante. La integral impropia puede expresarse como una integral definida por su simple propiedad de simetría (dado que la función es simétrica y la integral en la recta real es igual a \(1\))

\[ \int_2^\infty \frac{dx}{\pi(1+x^2)}=\frac{1}{2}-\int_0^2\frac{dx}{\pi(1+x^2)} . \] De esta expresión, una aproximación natural sería

\[ p_3 = \frac{1}{2}-\frac{1}{R}\sum_{i=1}^R h_3(2U_i), ~~~~~~\text{where}~h_3(x)=\frac{2}{\pi(1+x^2)} . \]

Con un millón de simulaciones, se obtiene una estimación de 0.14756 con error estándar 0.169 (divido por 1000). Se puede probar que la varianza de \(p_3\) es del orden \(0.0285/R\).

Finalmente, también se puede considerar algún cambio de variable en la integral

\[ \int_2^\infty \frac{dx}{\pi(1+x^2)}=\int_0^{1/2}\frac{y^{-2}dy}{\pi(1-y^{-2})} . \] De esta expresión, una aproximación natural sería

\[ p_4 = \frac{1}{R}\sum_{i=1}^R h_4(U_i/2),~~~~~\text{where}~h_4(x)=\frac{1}{2\pi(1+x^2)} . \] La expresión parece bastante similar a la anterior,

Con un millón de simulaciones, se obtiene una estimación de 0.14759 con error estándar 0.01 (dividido por 1000). Se puede probar que la varianza de \(p_4\) es de orden \(0.00009/R\), que es mucho menor que los valores obtenidos hasta ahora!

Tabla 6.1 resume las cuatro elecciones de \(h(\cdot)\) y \(F(\cdot)\) para aproximar \(\Pr[X>2] =\) 0.14758. El error estándar varía notablemente. Por tanto, si se desea un determinado grado de precisión, entonces el número de simulaciones depende mucho de cómo se escriban las integrales que se desean aproximar.

Tabla 6.1. Resumen de las cuatro elecciones para aproximar \(\Pr[X>2]\).
Estimador Definición Función de soporte Estimación Error estándar
\(p_1\) \(\frac{1}{R}\sum_{i=1}^R \mathrm{I}(F^{-1}(U_i)>2)\) \(~~~~~~F^{-1}(u)=\tan \left( \pi(u-0.5) \right)~~~~~~~\) 0.147439 0.000355
\(p_2\) \(\frac{1}{2R}\sum_{i=1}^R \mathrm{I}(|F^{-1}(U_i)|>2)\) \(F^{-1}(u)=\tan \left( \pi(u-0.5) \right)\) 0.147477 0.000228
\(p_3\) \(\frac{1}{2}-\frac{1}{R}\sum_{i=1}^R h_3(2U_i)\) \(h_3(x)=\frac{2}{\pi(1+x^2)}\) 0.147558 0.000169
\(p_4\) \(\frac{1}{R}\sum_{i=1}^R h_4(U_i/2)\) \(h_4(x)=\frac{1}{2\pi(1+x^2)}\) 0.147587 0.000010

6.1.4 Simulación e inferencia estadística

Las simulaciones no solo ayudan a aproximar valores esperados, sino que también son útiles para calcular otros aspectos de las funciones de distribución. En particular, son muy útiles cuando las distribuciones de los estadísticos de prueba son muy complicadas de derivar; en este caso, se pueden usar simulaciones para aproximar la distribución de referencia. Se ilustra esto con el test de Kolmogorov-Smirnov que se presenta en la Sección 4.1.2.2.

Ejemplo. 6.1.10. Distribución del test de Kolmogorov-Smirnov. Se tiene disponible \(n=100\) observaciones \(\{x_1,\cdots,x_n\}\) que, sin que lo sepa el analista, han sido generadas por una distribución gamma de parámetros \(\alpha = 6\) y \(\theta=2\). El analista cree que los datos provienen de una distribución lognormal con parámetros 1 y 0.4 y desearía comprobar esta hipótesis.

El primer paso es visualizar los datos.

Se muestra el código R para establecer la visualización

A partir de aquí, la Figura 6.5 proporciona un gráfico del histograma y distribución empírica. A modo de referencia, se superpone con línea rojas discontinua la distribución lognormal.

par(mfrow=c(1,2))
hist(x,probability = TRUE,main="Histogram", col="light blue",border="white",xlim=c(0,7),ylim=c(0,.4))
lines(u,dlnorm(u,1,.4),col="red",lty=2)
plot(vx,vy,type="l",xlab="x",ylab="Cumulative Distribution",main="Empirical cdf")
lines(u,plnorm(u,1,.4),col="red",lty=2)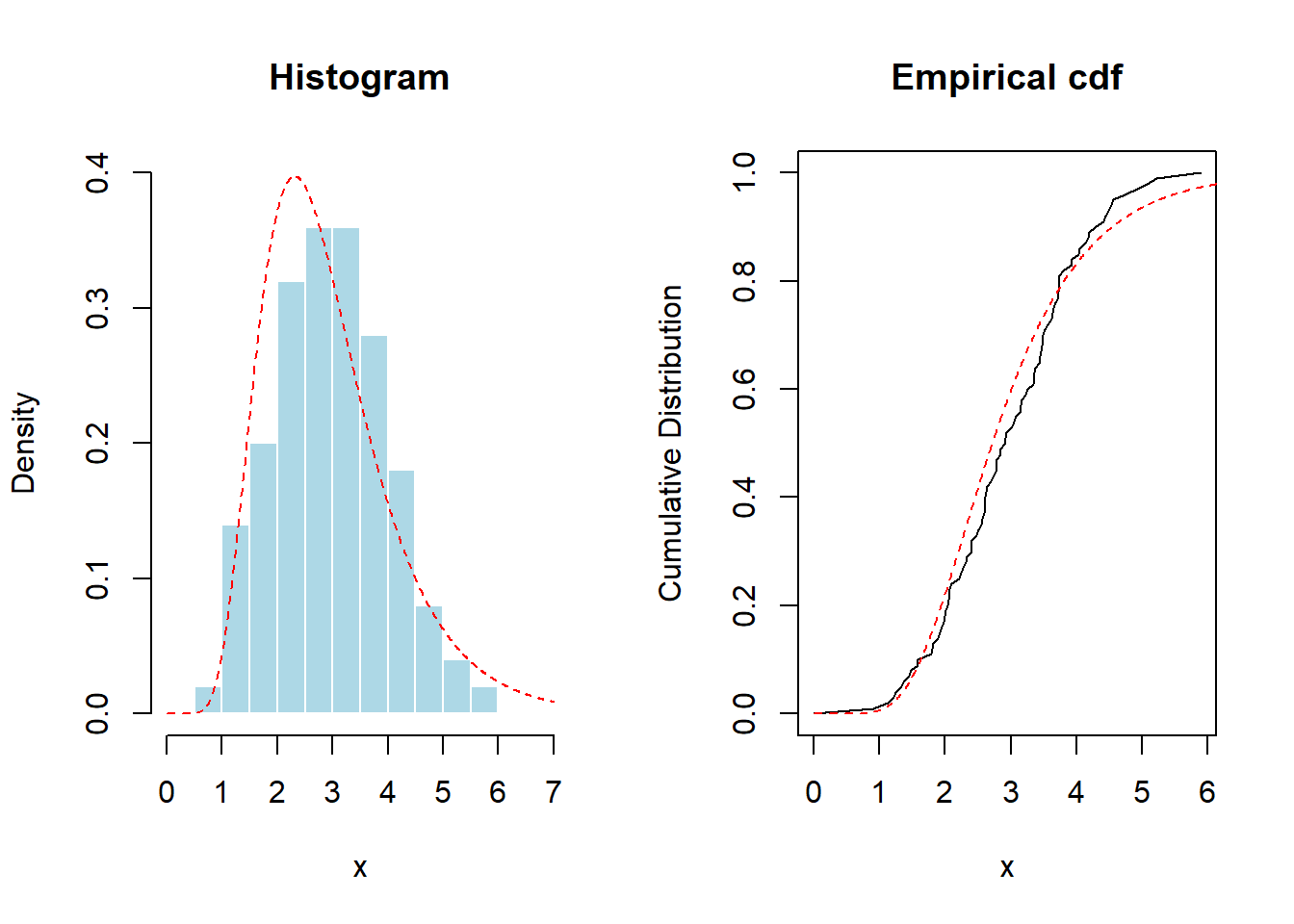
Histograma y función de distribución empírica de los datos usados en el test de Kolmogorov-Smirnov. Las líneas rojas discontinuas son ajustadas en base a una (incorrecta) hipótesis de distribución lognormal.

Figure 6.5: Histograma y función de distribución empírica de los datos usados en el test de Kolmogorov-Smirnov. Las líneas rojas discontinuas son ajustadas en base a una (incorrecta) hipótesis de distribución lognormal.

Es necesario recordad qeu el estadístico de Kolmogorov-Smirnov es igual a la mayor discrepancia entre la distribución empírica y la correspondiente a la hipótesis. Esto es \(\max_x |F_n(x)-F_0(x)|\), donde \(F_0\) es la distribución lognormal de la hipótesis. Se puede calcular esto de forma directa como:

Se muestra el código R para el cálculo directo del estadístico KS

Afortunadamente, para la distribución lognormal, R ha construido test que permiten determinar esto sin necesidad de realizar una programación complicada:

ks.test(x, plnorm, mean=1, sd=0.4)

    One-sample Kolmogorov-Smirnov test

data:  x
D = 0.097037, p-value = 0.3031
alternative hypothesis: two-sided

Sin embargo, para muchas distribuciones de interés actuarial, no se dispone de programas pre-construidos. Se puede usar la simulación para comprobar la relevancia de un estadístico de prueba. En concreto, para calcular el \(p\)-valor, se generan miles de muestras aleatorias de una distribución \(LN(1,0.4)\) (con el mismo tamaño), y se calcula empíricamente la distribución del estadístico,

Se muestra el código R para la distribución simulada del estadístico KS 
hist(d_KS,probability = TRUE,col="light blue",border="white",xlab="Estadístico de prueba",main="")
lines(density(d_KS),col="red")
abline(v=D(x,function(x) plnorm(x,1,.4)),lty=2,col="red")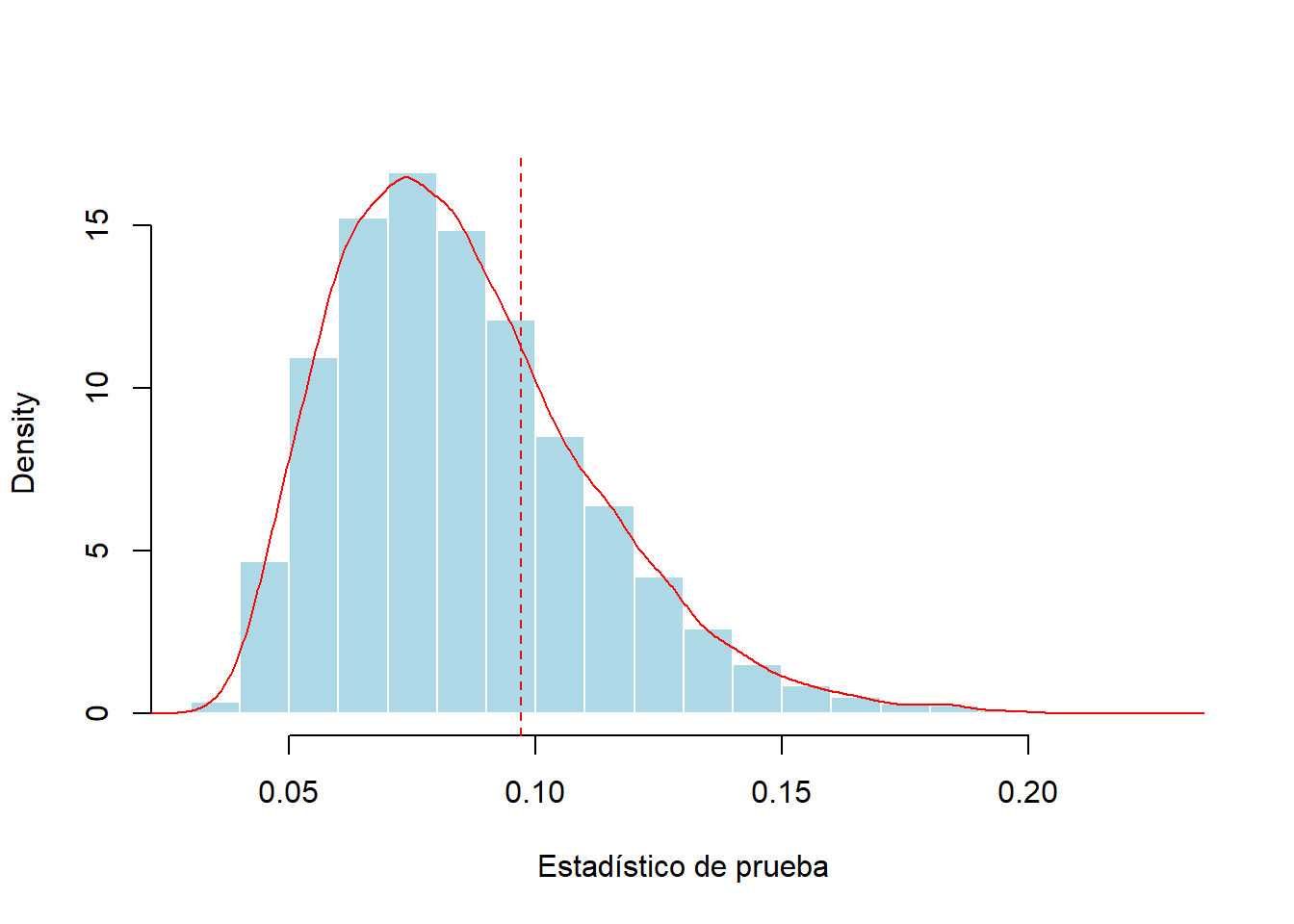
Distribución simulada del estadístico de prueba de Kolmogorov-Smirnov. La línea roja discontinua vertical marca el estadístico de prueba para una muestra de 100.

Figure 6.6: Distribución simulada del estadístico de prueba de Kolmogorov-Smirnov. La línea roja discontinua vertical marca el estadístico de prueba para una muestra de 100.

La distribución simulada basada en 10,000 muestras aleatorias se resume en la Figura 6.6. Aquí, el estadístico excede el valor empírico (0.09704) en 28.43% de los escenarios, mientras que el \(p\)-valor teórico es 0.3031. Tanto para la simulación como para los \(p\)-valores teóricos, las conclusiones son las mismas; los datos no proporcionan evidencia suficiente para rechazar la hipótesis de la distribución lognormal.

Aunque se trate solo de una aproximación, el enfoque basado en la simulación funciona en una gran variedad de distribuciones y estadísticos de prueba sin necesitar desarrollar los detalles de la teoría de base en cada situación. Se puede resumir el procedimiento para desarrollar distribuciones simuladas y p-valores como sigue:

  1. Obtén una muestra de tamaño n, es decir, \(X_1, \ldots, X_n\), de una función de distribución conocida \(F\). Calcula el estadístico de interés, denotado por \(\hat{\theta}(X_1, \ldots, X_n)\). Se le llama \(\hat{\theta}^r\) para la réplica résima.
  2. Se repite \(r=1, \ldots, R\) veces para obtener una muestra de estadísticos, \(\hat{\theta}^1, \ldots,\hat{\theta}^R\).
  3. De la muestra de estadísticos en el paso 2, \(\{\hat{\theta}^1, \ldots,\hat{\theta}^R\}\), se calcula una medida de resumen de interés, como el p-valor.

6.2 Bootstrapping y Remuestreo

En esta sección, se muestra como:

  • Generar una distribución no paramétrica bootstrap para un estadístico de interés
  • Usar la distribución bootstrap para generar estimaciones de la precisión del estadístico de interés, incluyendo sesgo, desviaciones estándar, e intervalos de confianza
  • Realizar análisis bootstrap para distribuciones paramétricas

6.2.1 Fundamentos del Bootstrap

La simulación presentada hasta ahora se basa en un muestreo a partir de una distribución conocida. La Sección 6.1 mostró como usar técnicas de simulación para obtener muestras y calcular cantidades de estas distribuciones conocidas. Sin embargo, la ciencia estadística se dedica a proporcionar inferencias sobre distribuciones que son desconocidas. Se recopilan estadísticos de resumen basados en esta distribución desconocida de una población. Pero, ¿cómo se puede realizar un muestreo de una distribución desconocida?

Naturalmente, no se pueden simular valores de una distribución desconocida pero sí que se pueden obtener valores de una muestra de observaciones. Si la muestra es una buena representación de una población, entonces nuestras extracciones simuladas de una muestra se aproximan bien a las extracciones simuladas de una población. El proceso de obtener una muestra de una muestra se llama remuestreo o bootstrapping.

El término bootstrap proviene de la frase (en inglés) “pulling oneself up by one’s bootstraps” (Efron, 1979). En el remuestreo, la muestra original juega el papel de la población y las estimaciones obtenidas a partir de la muestra juegan el papel de los verdaderos parámetros de la población.

El algoritmo de remuestreo es el mismo que el introducido en la Sección 6.1.4 excepto que ahora usa extracciones simuladas de la muestra. Es común usar \(\{X_1, \ldots, X_n\}\) para denotar la muestra original y \(\{X_1^*, \ldots, X_n^*\}\) para los valores simulados. Las extracciones se realizan con reemplazamiento para que los valores simulados sean independientes entre ellos, la misma suposición que para la muestra original. Para cada muestra, también se realizan n extracciones simuladas, el mismo valor que el tamaño muestral. Para distinguir este proceso de la simulación, es común usar B (de bootstrap) para representar el número de muestras simuladas. También se puede escribir \(\{X_1^{(b)}, \ldots, X_n^{(b)}\}\), \(b=1,\ldots, B\) lo cual resulta más claro. Hay dos métodos básicos de remuestreo, model-free y model-based (tomando sus nombres en inglés), que son, respectivamente, no paramétrico y paramétrico. En el enfoque no paramétrico, no se hace ninguna suposición sobre la distribución de la población de origen. Las extracciones simuladas provienen de la función de distribución empírica \(F_n(\cdot)\), por lo que cada extracción proviene de \(\{X_1, \ldots, X_n\}\) con probabilidad 1/n.

Por contra, para el enfoque paramétrico, se asume que se tiene conocimiento de la familia de la distribución F. La muestra original \(X_1, \ldots, X_n\) se usa para estimar los parámetros de esa familia, es decir, \(\hat{\theta}\). Entonces, las extracciones simuladas se toman de \(F(\hat{\theta})\). En la Sección 6.2.4 se comenta este enfoque con más detalle.

Bootstrap no paramétrico

La idea del bootstrap no paramétrico es usar el método inverso en \(F_n\), la función de distribución empírica acumulada, representada en la Figura 6.7.

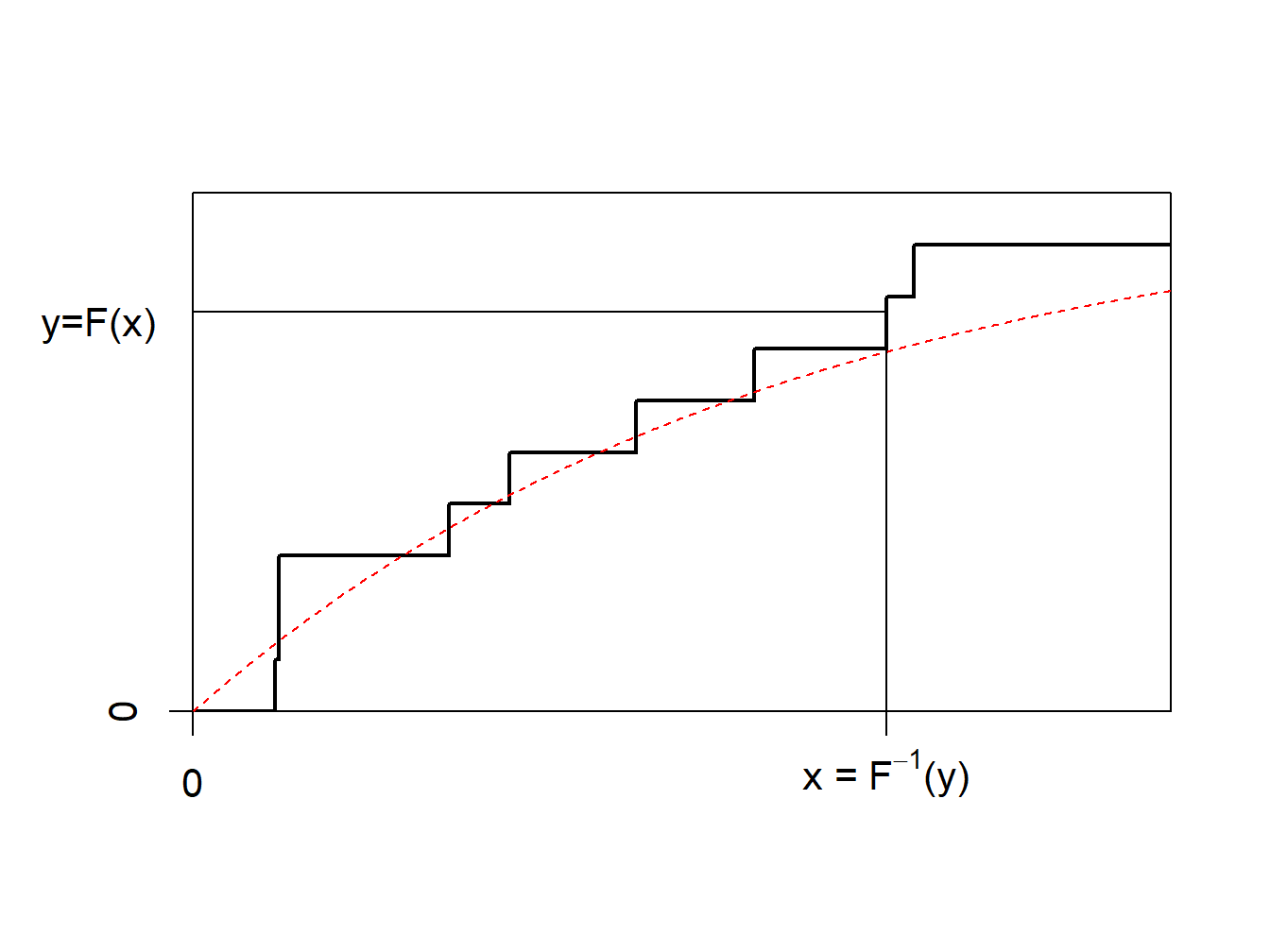
Inversa de la función de distribución empírica

Figure 6.7: Inversa de la función de distribución empírica

Debido a que \(F_n\) es una función escalonada, \(F_n^{-1}\) toma valores en \(\{x_1,\cdots,x_n\}\). Más concretamente, puede verse la ilustración de la Figura 6.8. - si \(y\in(0,1/n)\) (con probabilidad \(1/n\)) se extrae el valor más pequeño (\(\min\{x_i\}\)) - si \(y\in(1/n,2/n)\) (con probabilidad \(1/n\)) se extrae el segundo valor más pequeño, - … - si \(y\in((n-1)/n,1)\) (con probabilidad \(1/n\)) se extrae el mayor valor (\(\max\{x_i\}\)).

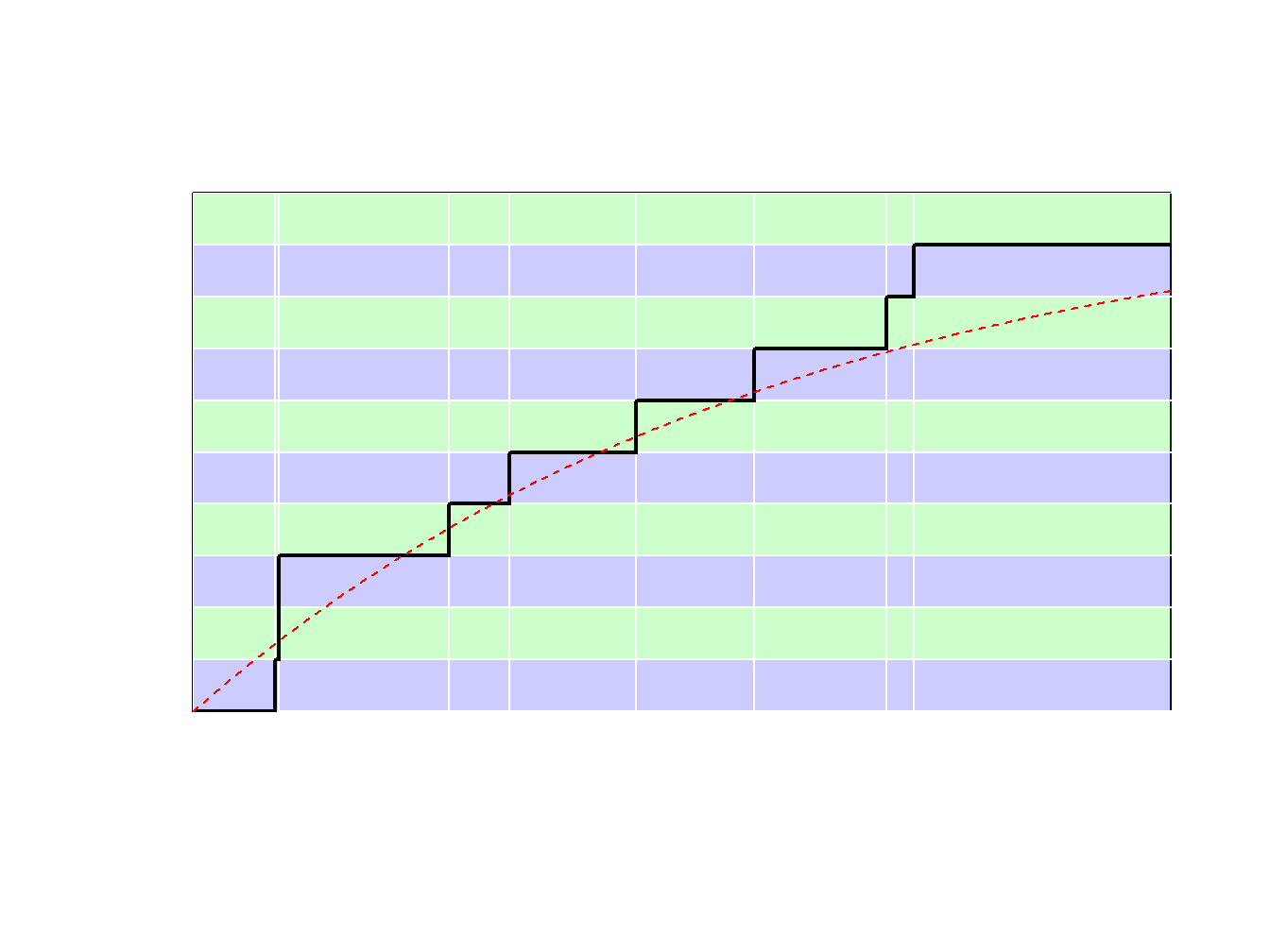
Inversa de la función de distribución empírica

Figure 6.8: Inversa de la función de distribución empírica

Usar el método inverso con \(F_n\) significa muestrear a partir de \(\{x_1,\cdots,x_n\}\), con probabilidad \(1/n\). Generar una muestra bootstrap de tamaño \(B\) significa muestrear a partir de \(\{x_1,\cdots,x_n\}\), con probabilidad \(1/n\), con reemplazamiento. A continuación, se puede consultar el siguiente código de R ilustrativo.

Muestra el código R para crear una muestra con Bootstrap 
[1] 2.6164 5.7394 5.7394 2.6164 2.6164 7.0899 0.8823 5.7394

Se observa que el valor 0.8388 se ha obtenido tres veces.

6.2.2 Precisión del bootstrap: Sesgo, desviación estándar, y MSE (error cuadrático medio, en sus siglas en inglés)

Se resume el procedimiento para el bootstrap no paramétrico como sigue:

  1. Para la muestra \(\{X_1, \ldots, X_n\}\), se extrae una muestra de tamaño n (con reemplazamiento), es decir, \(X_1^*, \ldots, X_n^*\). De las extracciones simuladas se calcula el estadístico de interés, denotado como \(\hat{\theta}(X_1^*, \ldots, X_n^*)\). Se denomina \(\hat{\theta}_b^*\) para la réplica bésima.
  2. Se repite esto \(b=1, \ldots, B\) veces para obtener una muestra de estadísticos, \(\hat{\theta}_1^*, \ldots,\hat{\theta}_B^*\).
  3. Para la muestra de estadísticos en el paso 2, \(\{\hat{\theta}_1^*, \ldots, \hat{\theta}_B^*\}\), se calcula una medida de resumen de interés.

En esta sección, se centra el interés en tres medidas de resumen, el sesgo, la desviación estándar, y el error cuadrático medio (MSE). Tabla 6.2 resume estas tres medidas. Aquí, \(\overline{\hat{\theta^*}}\) es el promedio de \(\{\hat{\theta}_1^*, \ldots,\hat{\theta}_B^*\}\).

\[ {\small \begin{matrix} \text{Tabla 6.2. Medidas de resumen bootstrap}\\ \begin{array}{l|c|c|c} \hline \text{Medida de la población}& \text{Definición de la población}&\text{Aproximación bootstrap }&\text{Símbolo bootstrap}\\ \hline \text{Sesgo} & \mathrm{E}(\hat{\theta})-\theta&\overline{\hat{\theta^*}}-\hat{\theta}& Bias_{boot}(\hat{\theta}) \\\hline \text{Desviación estándar} & \sqrt{\mathrm{Var}(\hat{\theta})} & \sqrt{\frac{1}{B-1} \sum_{b=1}^{B}\left(\hat{\theta}_b^* -\overline{\hat{\theta^*}} \right) ^2}&s_{boot}(\hat{\theta}) \\\hline \text{Error cuadrático medio} &\mathrm{E}(\hat{\theta}-\theta)^2 & \frac{1}{B} \sum_{b=1}^{B}\left(\hat{\theta}_b^* -\hat{\theta} \right)^2&MSE_{boot}(\hat{\theta})\\ \hline \end{array}\end{matrix} } \]

Ejemplo 6.2.1. Siniestros con daños corporales y ratio de eliminación de pérdida. Para mostrar cómo el bootstrap puede usarse para cuantificar la precisión de los estimadores, se retoma el Ejemplo 4.1.11 sobre los datos de siniestros con daños corporales donde se introdujo el estimador no paramétrico de la ratio de eliminación de pérdidas.

Tabla 6.3 resume los resultados de la estimación bootstrap. Por ejemplo, para \(d=14000\), se vió en el Ejemplo 4.1.11 que la estimación no paramétrica de LER es 0.97678. Este valor tiene un sesgo estimado de 0.00018 con una desviación estándar de 0.00701. Para algunas aplicaciones, se puede desear aplicar el sesgo estimado a la estimación original para obtener un estimador corregido por el sesgo. En ello se centra el próximo ejemplo. Para esta ilustración, el sesgo es pequeño por lo que dicha corrección no es relevante.

Muestra el código R para la estimaciones bootstrap de LER

Tabla 6.3. Estimaciones bootstrap para el LER en franquicias seleccionadas
d Estimación NP Sesgo bootstrap Bootstrap SD Límite inferior del CI (intervalo de confianza, en sus siglas en inglés) Normal al 95% Límite superior del CI Normal al 95%
4000 0.54113 0.00011 0.01237 0.51678 0.56527
5000 0.64960 0.00027 0.01412 0.62166 0.67700
10500 0.93563 0.00004 0.01017 0.91567 0.95553
11500 0.95281 -0.00003 0.00941 0.93439 0.97128
14000 0.97678 0.00016 0.00687 0.96316 0.99008
18500 0.99382 0.00014 0.00331 0.98719 1.00017

La desviación estándar bootstrap proporciona una medida de precisión. Para una aplicación de las desviaciones estándar, se puede usar la aproximación normal para crear un intervalo de confianza. Por ejemplo, la función de R boot.ci produce intervalos de confianza normales al 95%. Se producen creando un intervalo de dos veces la amplitud de 1.95994 desviaciones estándar bootstrap, centrado en el estimador corregido por el sesgo (1.95994 es el cuantil 97.5 de la distribución normal estándar). Por ejemplo, el intervalo inferior del 95% CI normal en \(d=14000\) es \((0.97678-0.00018)- 1.95994*0.00701\) \(= 0.96286\). Más adelante se comentan los intervalos de confianza bootstrap en la siguiente sección.

Ejemplo 6.2.2. Estimar \(\exp(\mu)\).

El bootstrap se puede usar para cuantificar el sesgo de un estimador, por ejemplo. Consideramos una muestra \(\mathbf{x}=\{x_1,\cdots,x_n\}\) que es iid con media \(\mu\).

sample_x <- c(2.46,2.80,3.28,3.86,2.85,3.67,3.37,3.40,5.22,2.55,
              2.79,4.50,3.37,2.88,1.44,2.56,2.00,2.07,2.19,1.77)

Se supone que la cantidad de interés es \(\theta=\exp(\mu)\). Un estimador natural sería \(\widehat{\theta}_1=\exp(\overline{x})\). Este estimador tiene sesgo (debido a la desigualdad Jensen) pero es asintóticamente insesgado. Para nuestra muestra, la estimación es como se muestra a continuación.

(theta_1 <- exp(mean(sample_x)))
[1] 19.13463

Se puede usar el teorema central del límite para obtener una corrección usando

\[ \overline{X}\approx\mathcal{N}\left(\mu,\frac{\sigma^2}{n}\right)\text{ where }\sigma^2=\text{Var}[X_i] , \] De modo que, con la función generatriz de momentos normal, se tiene

\[ \mathrm{E}~\exp[\overline{X}] \approx \exp\left(\mu+\frac{\sigma^2}{2n}\right) . \] Por tanto, se puede considerar

\[ \widehat{\theta}_2=\exp\left(\overline{x}-\frac{\widehat{\sigma}^2}{2n}\right) . \] Para nuestros datos, resulta lo siguiente.

n <- length(sample_x)
(theta_2 <- exp(mean(sample_x)-var(sample_x)/(2*n)))
[1] 18.73334

Otra estrategia (que no vamos a desarrollar aquí) sería usar una aproximación de Taylor para obtener un estimador más preciso (como en el método delta),

\[ g(\overline{x})=g(\mu)+(\overline{x}-\mu)g'(\mu)+(\overline{x}-\mu)^2\frac{g''(\mu)}{2}+\cdots \] La alternativa que se explora es usar una estrategia bootstrap: dada una muestra bootstrap, \(\mathbf{x}^{\ast}_{b}\), sea \(\overline{x}^{\ast}_{b}\) dsu media, y se establece

\[ \widehat{\theta}_3=\frac{1}{B}\sum_{b=1}^B\exp(\overline{x}^{\ast}_{b}) . \] Para implementarlo, se proporciona el siguiente código.

Se muestra el código R para crear muestras bootstrap

Entonces, se puede plot(results) y print(results) para observar lo siguiente.

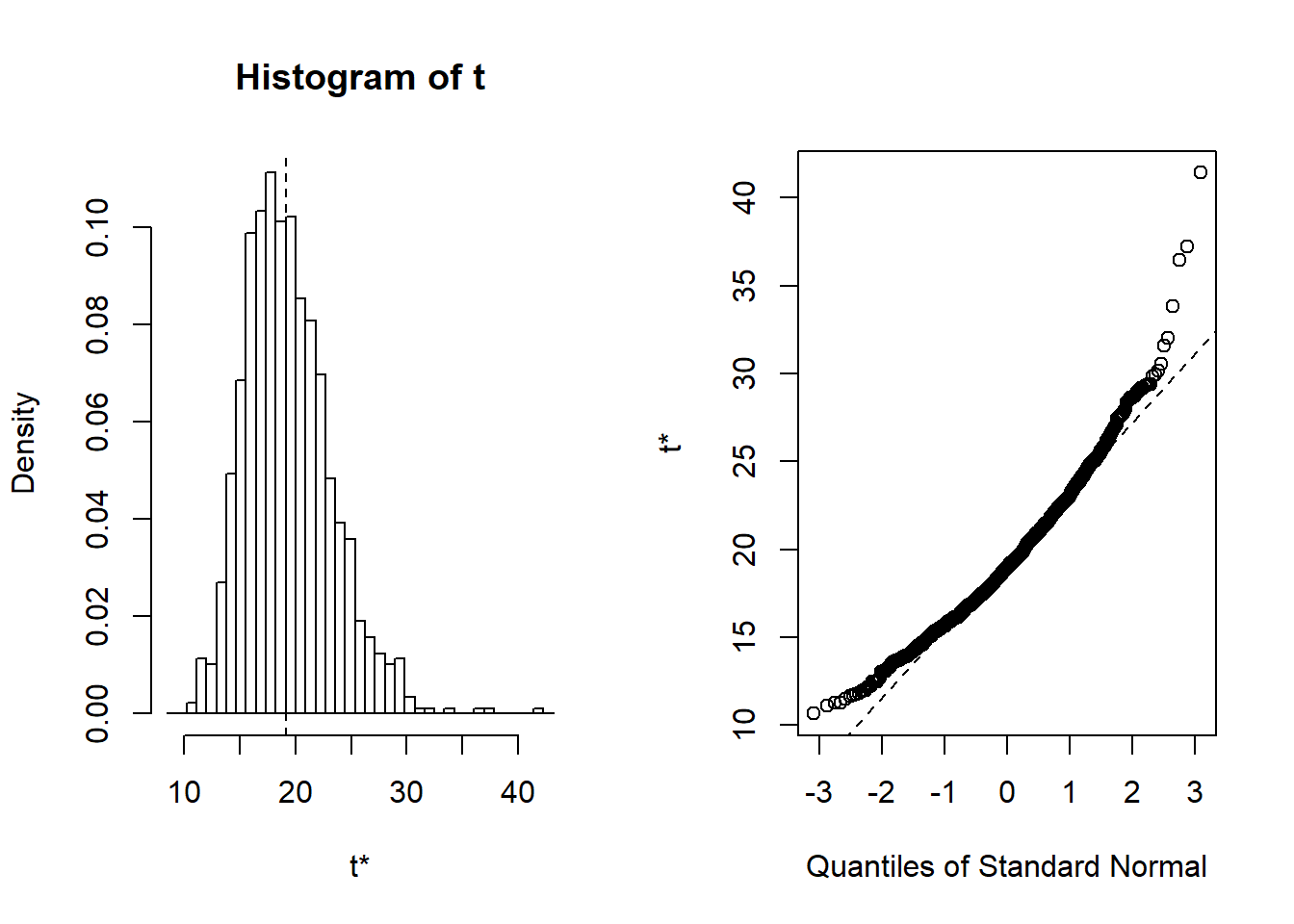
Distribución de las réplicas bootstrap. El panel de la izquierda es un histograma de réplicas. El panel de la derecha es un gráfico cuantil-cuantil, que compara la distribución bootstrap con la distribución normal estándar.

Figure 6.9: Distribución de las réplicas bootstrap. El panel de la izquierda es un histograma de réplicas. El panel de la derecha es un gráfico cuantil-cuantil, que compara la distribución bootstrap con la distribución normal estándar. 


ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = sample_x, statistic = function(y, indices) exp(mean(y[indices])), 
    R = 1000)


Bootstrap Statistics :
    original    bias    std. error
t1* 19.13463 0.2536551    3.909725

Esto resulta en tres estimadores, el estimador bruto \(\widehat{\theta}_1=\) 19.135, la corrección de segundo orden \(\widehat{\theta}_2=\) 18.733, y el estimador bootstrap \(\widehat{\theta}_3=\) 19.388. ¿Como funciona esto con diferentes tamaños de muestra? Ahora se supone que \(x_i\)’s son generadas a partir de una distribución lognormal \(LN(0,1)\), de modo que \(\mu = \exp(0 + 1/2) = 1.648721\) y \(\theta = \exp(1.648721)\) \(= 5.200326\). Se usa la simulación para extraer los tamaños muestrales pero luego se actúa como si fueran un conjunto de observaciones realizadas. Véase el siguiente código ilustrativo.

Se muestral el código R para crear muestras bootstrap

Los resultados de la comparación se resumen en la Figura 6.10. Esta figura muestra que el estimador bootstrap está más cerca del verdadero valor del parámetro para casi todos los tamaños muestrales. El sesgo de los tres estimadores decrece al aumentar el tamaño muestral.

matplot(VN,t(Est),type="l", col=2:4, lty=2:4, ylim=exp(exp(1/2))+c(-1,1),
        xlab="sample size (n)", ylab="estimator")
abline(h=exp(exp(1/2)),lty=1, col=1)
legend("topleft", c("estimador bruto", "corrección de segundo orden", "bootstrap"),
       col=2:4,lty=2:4, bty="n")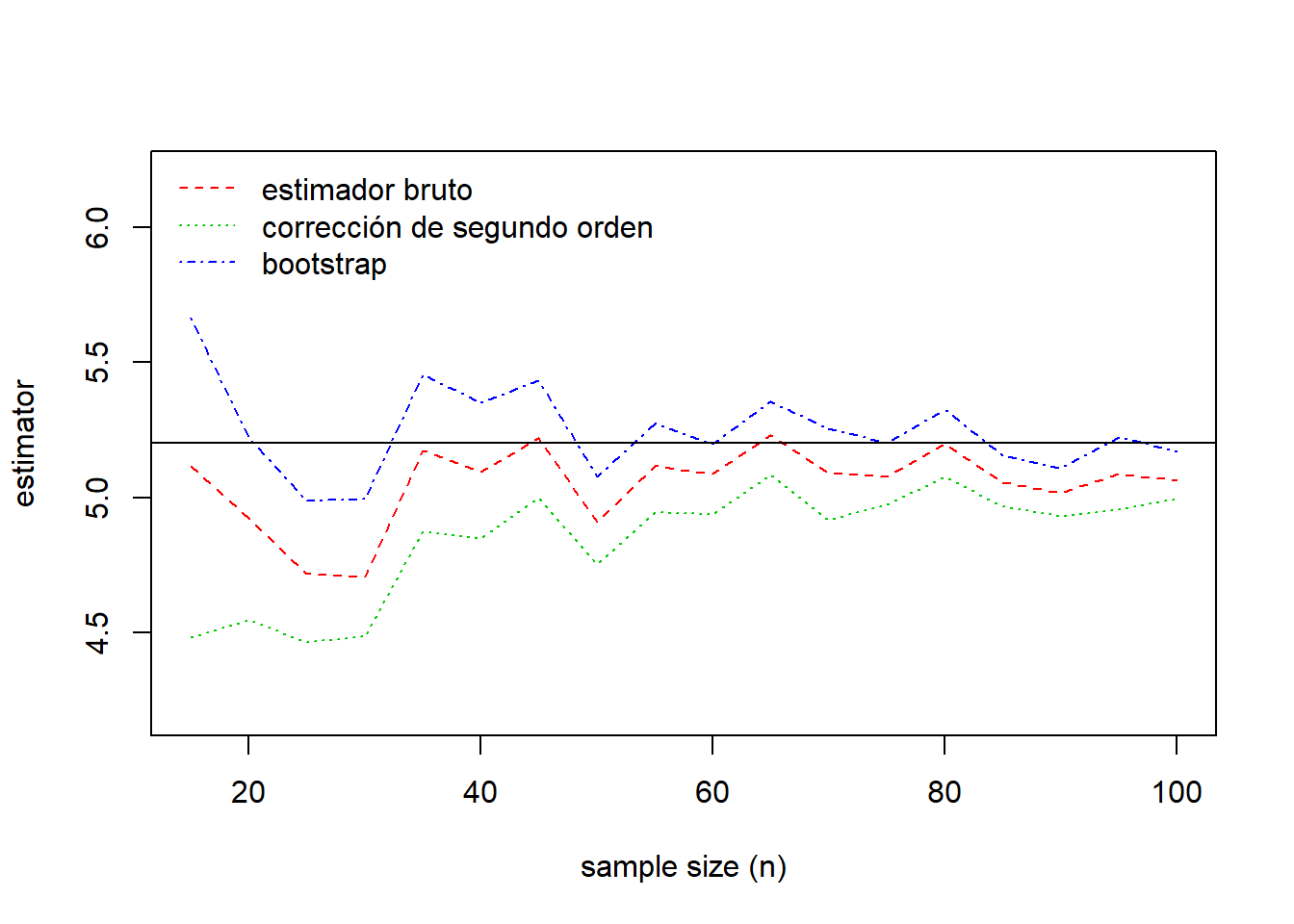
Comparación de estimaciones. El verdadero valor del parámetro viene dado por la línea continua horizontal en 5.20.

Figure 6.10: Comparación de estimaciones. El verdadero valor del parámetro viene dado por la línea continua horizontal en 5.20.

6.2.3 Intervalos de confianza

El procedimiento bootstrap genera B réplicas \(\hat{\theta}_1^*, \ldots,\hat{\theta}_B^*\) del estimador \(\hat{\theta}\). En el Ejemplo 6.2.1, se mostró cómo usar las aproximaciones a la normal estándar para crear intervalos de confianza de los parámetros de interés. Sin embargo, dado que el interés se centra en usar el bootstrap para evitar confiar en supuestos de aproximación a la normal, no sorprende que haya disponibilidad de intervalos de confianza alternativos.

Para un estimador \(\hat{\theta}\), el intervalo de confianza básico bootstrap es

\[\begin{equation} \left(2 \hat{\theta} - q_U, 2 \hat{\theta} - q_L \right) , \tag{6.2} \end{equation}\]

donde \(q_L\) y \(q_U\) son los cuantiles al 2.5% inferior y superior de la muestra bootstrap \(\hat{\theta}_1^*, \ldots,\hat{\theta}_B^*\). Para ver de dónde viene esto, se toma como punto de partida la idea de que \((q_L, q_U)\) proporciona un intervalo al 95% para \(\hat{\theta}_1^*, \ldots,\hat{\theta}_B^*\). Por tanto, para un \(\hat{\theta}_b^*\) aleatorio, hay un 95% de probabilidades de que \(q_L \le \hat{\theta}_b^* \le q_U\). Revirtiendo las desigualdades y añadiendo \(\hat{\theta}\) a cada lado se obtiene un intervalo al 95%

\[ \hat{\theta} -q_U \le \hat{\theta} - \hat{\theta}_b^* \le \hat{\theta} -q_L . \] Por tanto, \(\left( \hat{\theta}-q_U, \hat{\theta} -q_L\right)\) es un intervalo al 95% para \(\hat{\theta} - \hat{\theta}_b^*\). La idea de la aproximación bootstrap indica que ello es también un intervalo al 95% para \(\theta - \hat{\theta}\). Añadiendo \(\hat{\theta}\) a cada lado da un intervalo al 95% en la ecuación (6.2).

Hay muchos intervalos bootstrap alternativos. El más sencillo de explicar es el intervalo basado en los percentiles bootstrap que se define como \(\left(q_L, q_U\right)\). No obstante, presenta la desventaja de tener un comportamiento potencialmente pobre en las colas, lo cual puede ser un inconveniente en algunos problemas actuariales de interés.

Ejemplo 6.2.3. Siniestros con daños corporales y medidas de riesgo. Para ver cómo funcionan los intervalos de confianza bootstrap, se retoma los datos sobre siniestros del automóvil con daños corporales considerados en el Ejemplo 6.2.1. En lugar de la ratio de eliminación de pérdida, se desea estimar el percentil al 95% \(F^{-1}(0.95)\) y una medida definida como \[ TVaR_{0.95)}[X] = \mathrm{E}[X | X > F^{-1}(0.95)] . \] Esta medida se llama tail value-at-risk; es el valor esperado de \(X\) condicionado a que \(X\) exceda el percentil al 95%. En la Sección 10.2 se explica como los cuantiles y el tail value-at-risk son los dos ejemplos más importantes de las llamadas medidas de riesgo. Por el momento, se considerarán simplemente como medidas que se quieren estimar. Para el percentil, se usa el estimador no paramétrico \(F^{-1}_n(0.95)\) definido en la Sección 4.1.1.3. Para el tail value-at-risk, se usa el principio plug-in para definir el estimador no paramétrico

\[ TVaR_{n,0.95}[X] = \frac{\sum_{i=1}^n X_i I(X_i > F^{-1}_n(0.95))}{\sum_{i=1}^n I(X_i > F^{-1}_n(0.95))} ~. \] En esta expresión, el denominador cuenta el número de observaciones que exceden el percentil al 95% \(F^{-1}_n(0.95)\). El numerador suma las pérdidas para aquellas observaciones que exceden \(F^{-1}_n(0.95)\). Tabla 6.4 resume el estimador para para fracciones seleccionadas.

Se muestra el código R para crear muestras basadas en el cuantil Bootstrap

Tabla 6.4. Estimaciones bootstrap de cuantiles en fracciones seleccionadas
Fracción Estimación NP Sesgo bootstrap Bootstrap SD Límite inferior del CI Normal al 95% Límite superior del CI Normal al 95% Límite inferior del CI básico al 95% Límite superior del CI básico al 95% Límite inferior del CI percentil al 95% Límite superior del CI percentil al 95%
0.50 6500.00 -128.02 200.36 6235.32 7020.72 6300.00 7000.00 6000.00 6700.00
0.80 9078.40 89.51 200.27 8596.38 9381.41 8533.20 9230.40 8926.40 9623.60
0.90 11454.00 55.95 480.66 10455.96 12340.13 10530.49 12415.00 10493.00 12377.51
0.95 13313.40 13.59 667.74 11991.07 14608.55 11509.70 14321.00 12305.80 15117.10
0.98 16758.72 101.46 1273.45 14161.34 19153.19 14517.44 19326.95 14190.49 19000.00

Por ejemplo, cuando la fracción es 0.50, se observa que los cuantiles al 2.5th por abajo y por arriba de las simulaciones bootstrap son \(q_L=\) 6000 y \(q_u=\) 6700, respectivamente. Ello forma el intervalo de confianza percentil bootstrap. Con el estimador no paramétrico 6500, se obtienen los límites inferiores y superiores de los intervalos de confianza básicos 6300 y 7000, respectivamente. La Tabla 6.4 también muestra las estimaciones bootstrap del sesgo, desviación estándar, y el intervalo de confianza normal, conceptos introducidos en la sección anterior.

La Tabla 6.5 muestra cálculos similares para el tail value-at-risk. En cada caso, se observa que la desviación estándar bootstrap aumenta a medida que la fracción aumenta. Ello es un reflejo de que cada vez hay menos observaciones disponibles para estimar los cuantiles a medida que la fracción aumenta, y por lo tanto hay una mayor imprecisión. La amplitud de los intervalos de confianza también aumenta. Resulta interesante ver que no parece haber el mismo patrón en las estimaciones del sesgo.

Se muestra el código R para crear muestras basadas en el TVar Bootstrap

Tabla 6.5. Estimación bootstrap del TVaR en niveles de riesgo seleccionados
Fracción Estimación NP Sesgo bootstrap Bootstrap SD Límite inferior del CI normal al 95% Límite superior del CI normal al 95% Límite inferior del CI básico al 95% Límite superior del CI básico al 95% Límite inferior del CI percentil al 95% Límite superior del CI Percentil al 95%
0.50 9794.69 -120.82 273.35 9379.74 10451.27 9355.14 10448.87 9140.51 10234.24
0.80 12454.18 30.68 481.88 11479.03 13367.96 11490.62 13378.52 11529.84 13417.74
0.90 14720.05 17.51 718.23 13294.82 16110.25 13255.45 16040.72 13399.38 16184.65
0.95 17072.43 5.99 1103.14 14904.31 19228.56 14924.50 19100.88 15043.97 19220.36
0.98 20140.56 73.43 1587.64 16955.40 23178.85 16942.36 22984.40 17296.71 23338.75

6.2.4 Bootstrap paramétrico

La idea del bootstrap no paramétrico es remuestrear extrayendo variables independientes a partir de la función de distribución acumulada empirica \(F_n\). Por otra parte, en el bootstrap paramétrico, se extraen variables independientes de \(F_{\widehat{\theta}}\) donde la distribución subyacente se asume que pertenece a una familia paramétrica \(\mathcal{F}=\{F_{\theta},\theta\in\Theta\}\). Normalmente, los parámetros de la distribución se estiman en base a una muestra y se denotan como \(\hat{\theta}\).

Ejemplo 6.2.4. Distribución Lognormal. Se considera nuevamente la base de datos

sample_x <- c(2.46,2.80,3.28,3.86,2.85,3.67,3.37,3.40,
              5.22,2.55,2.79,4.50,3.37,2.88,1.44,2.56,2.00,2.07,2.19,1.77)

El bootstrap clásico (no paramétrico) se basaba en muestras

x <- sample(sample_x,replace=TRUE)

Mientras que para el bootstrap paramétrico, se asume que la distribución de \(x_i\)’s es de una familia específica, por ejemplo la distribución lognormal.

library(MASS)
fit <- fitdistr(sample_x, dlnorm, list(meanlog = 1, sdlog = 1))
fit
    meanlog       sdlog   
  1.03630697   0.30593440 
 (0.06840901) (0.04837027)

Entonces se realiza la extracción partiendo de esta distribución.

x <- rlnorm(length(sample_x), meanlog=fit$estimate[1], sdlog=fit$estimate[2])
Se muestra el código R para muestras con bootstrap paramétrico

La Figura 6.11 compara las distribuciones bootstrap para el coeficiente de variación, una de ellas basada en el enfoque no paramétrico y la otra basada en el enfoque paramétrico, asumiendo una distribución lognormal.

plot(density(CV[,1]),col="red",main="",xlab="Coeficiente de variación", lty=1)
lines(density(CV[,2]),col="blue",lty=2)
abline(v=sd(sample_x)/mean(sample_x),lty=3)
legend("topright",c("nonparametric","parametric(LN)"),
       col=c("red","blue"),lty=1:2,bty="n")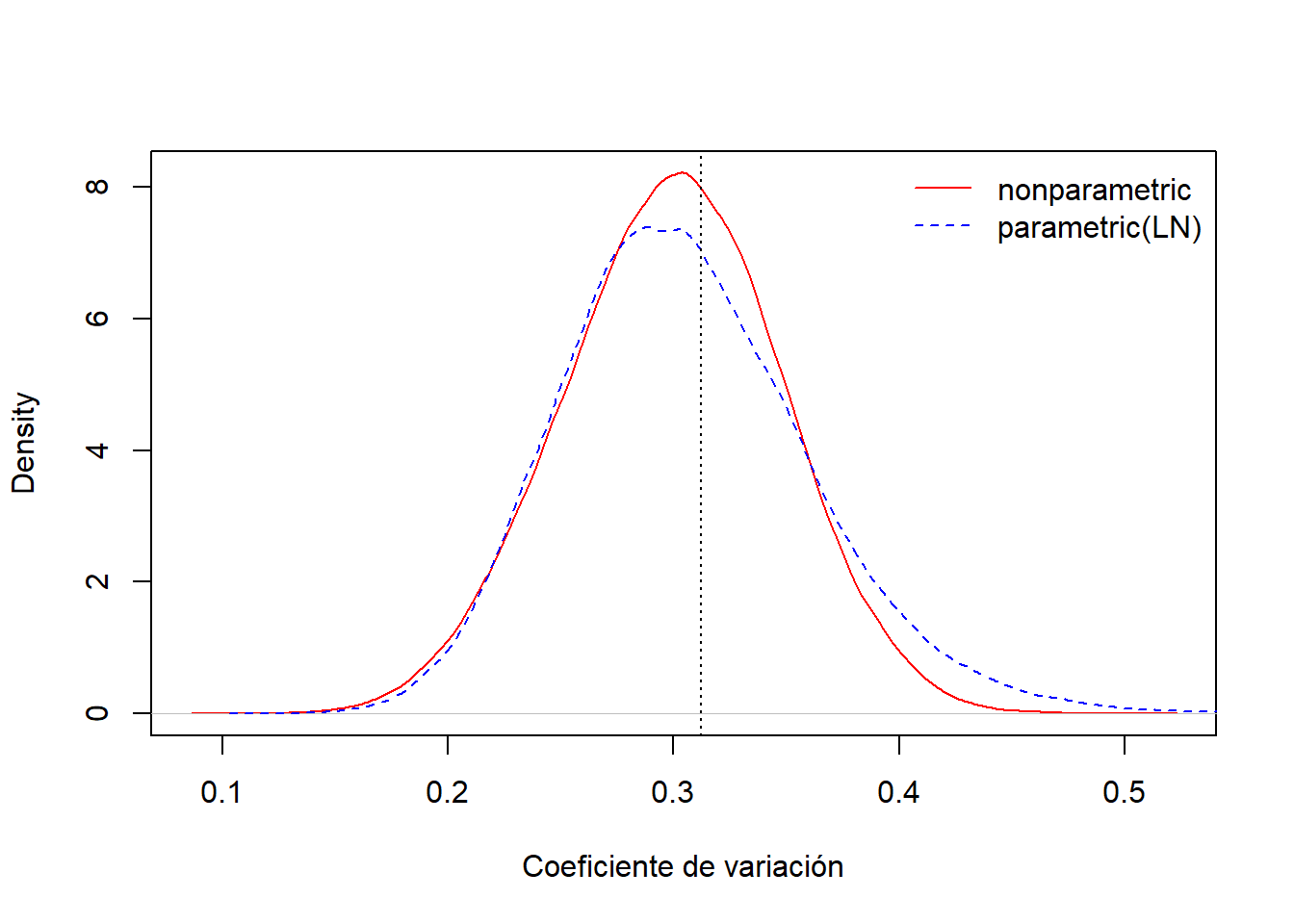
Comparación de las distribuciones Bootstrap no paramétrico y paramétrico para el coeficiente de variación

Figure 6.11: Comparación de las distribuciones Bootstrap no paramétrico y paramétrico para el coeficiente de variación

Ejemplo 6.2.5. Bootstrap de observaciones censuradas. El bootstrap paramétrico extrae realizaciones simuladas de una estimación paramétrica de una función de distribución. Del mismo modo, se pueden extraer realizaciones simuladas de la estimación de una función de distribución. A modo de ejemplo, se pueden realizar extracciones de estimaciones suavizadas de una función de distribución según lo introducido en la Sección 4.1.1.4. Otro caso especial, considerado aquí, es extraer una estimación del estimador de Kaplan-Meier introducido en la Sección 4.3.2.2. De esta forma, se pueden manejar observaciones que están censuradas.

Concretamente, se consideran nuevamente los datos sobre daños corporales de los Ejemplos 6.2.1 y 6.2.3 pero ahora se incluyen 17 siniestros que están censurados por límites en la póliza. En el Ejemplo 4.3.6, se usó esta base de datos completa para estimar el estimador de Kaplan-Meier de la función de supervivencia introducida en la Sección 4.3.2.2. La Tabla 6.6 presenta las estimaciones bootstrap de los cuantiles obtenidos de la estimación de la función de supervivencia Kaplan-Meier. Incluye las estimaciones de la precisión bootstrap, sesgo y desviación estándar, así como el intervalo de confianza básico al 95%.

Muestra el código R para las estimaciones Bootstrap Kaplan-Meier

Tabla 6.6. Estimaciones Bootstrap Kaplan-Meier de cuantiles en fracciones seleccionadas
Fracción Estimación KM NP Sesgo bootstrap Bootstrap SD Intervalo inferior del CI básico al 95% Intervalo superior del CI básico al 95%
0.50 6500 18.77 177.38 6067 6869
0.80 9500 167.08 429.59 8355 9949
0.90 12756 37.73 675.21 10812 13677
0.95 18500 Inf NaN 12500 22300
0.98 25000 Inf NaN -Inf 27308

Los resultados de la Tabla 6.6 son consistentes con los resultados de la submuestra no censurada de la Tabla 6.4. En la Tabla 6.6, se observa la dificultad de estimar cuantiles de fracciones grandes debido a la censura. No obstante, para fracciones de tamaños moderados (0.50, 0.80, y 0.90), las estimaciones del Kaplan-Meier no paramétrico (KM NP) del cuantil son consistentes con los resultados de la Tabla 6.4. La desviación estándar bootstrap es más pequeña al nivel de 0.50 (correspondiente a la mediana) pero mayor para los niveles 0.80 y 0.90. El análisis de los datos censurados resumido en Tabla 6.6 usa más datos que el análisis de la submuestra no censurada que aparece en la Tabla 6.4 pero también presenta dificultades para extraer información para cuantiles elevados.

6.3 Validación Cruzada

En esta sección, se muestra como:

  • Comparar y contrastar la validación cruzada a las técnicas de simulación y los métodos bootstrap.
  • Usar técnicas de validación cruzada para la selección de modelos
  • Explicar el método jackknife como caso especial de validación cruzada y calcular las estimaciones jackknife del sesgo y de los errores estándar

La validación cruzada, brevemente introducida en la Sección 4.2.4, es una técnica basada en simular resultados y por ello es conveniente pensar en su propósito en comparación con otras técnicas de simulación ya introducidas en este capítulo.

  • La simulación, o Monte-Carlo, introducida en la Sección 6.1, permite calcular valores esperados o otras medidas de resumen de distribuciones estadísticas, como \(p\)-valores, fácilmente.
  • El bootstrap, y otros métodos de remuestreo introducidos en la Sección 6.2, proporciona estimadores de la precisión, o variabilidad, de los estadísticos.
  • La validación cruzada es importante para valorar con qué precisión un modelo predictivo funcionará en la práctica.

Existe superposición, pero sin embargo es útil pensar acerca del objetivo general asociado con cada uno de los métodos.

Para presentar la validación cruzada, es conveniente recordar de la Sección 4.2 algunas de las ideas clave de la validación de modelos. Cuando se valora, o valida, un modelo, se mide el funcionamiento o desempeño del modelo en datos nuevos, o al menos no aquéllos que hayan sido usados para ajustar el modelo. Un enfoque clásico, descrito en la Sección 4.2.3, es dividir la muestra en dos partes: una parte (la base de datos de entrenamiento) se usa para ajustar el modelo y la otra (la base de datos de prueba) se usa para validar. Sin embargo, una limitación de este enfoque es que los resultados dependen de la partición; aunque la muestra general sea fija, la partición entre submuestras de entrenamiento y prueba varía aleatoriamente. Una muestra de entrenamiento diferente implica una estimación para los parámetros diferente. Unos parámetros diferentes para el modelo y una muestra de prueba diferente implican unos estadísticos de validación diferentes. Dos analistas pueden usar los mismos datos y los mismos modelos y pueden llegar a conclusiones diferentes sobre la viabilidad de un modelo (basado en diferentes particiones aleatorias), una situación frustrante.

6.3.1 Validación cruzada k-fold

Para mitigar esta dificultad, es común usar un enfoque de validación cruzada como el introducido en la Sección 4.2.4. La idea clave es emular el enfoque básico de entrenamiento/validación para la validación del modelo repitiéndolo muchas veces y tomando medias a partir de las diferentes particiones de los datos. Una ventaja clave es que el estadístico de validación no está ligado a un modelo paramétrico (o no paramétrico) específico – se puede usar un estadístico no paramétrico o un estadístico que tiene una interpretación económica – y puede ser usado para comparar modelos que no están anidados (diferente a como ocurre con los procedimientos de la ratio de verosimilitud).

Ejemplo 6.3.1. Fondo de propiedad de Wisconsin. Para los datos del fondo de propiedad de 2010 introducido en la Sección 1.3, se ajustan una gamma y una Pareto a los 1,377 datos de siniestros. Para ver en detalle la bondad de ajuste asociada se puede consultar el Apéndice Sección 15.4.4. Ahora se considera el estadístico de Kolmogorov-Smirnov introducido en la Sección 4.1.2.2. Cuando se realiza el ajuste sobre la totalidad de los datos, el estadístico de bondad del ajuste de Kolmogorov-Smirnov para la distribución gamma resulta ser 0.0478 y para la distribución de Pareto es 0.2639. El valor más bajo para la distribución de Pareto indica que esta distribución tiene mejor ajuste que la gamma.

Para ver cómo funciona la validación cruzada k-fold, se divide aleatoriamente los datos en \(k=8\) grupos, o folds (en inglés), cada uno con \(1377/8 \approx 172\) observaciones. Entonces, se ajustan una gamma y un modelo de Pareto a la base de datos con los primeros siete folds (sobre \(172*7 = 1204\) observaciones), se determinan los parámetros estimados, y entonces se usan estos modelos ajustados con los datos restantes para determinar el estadístico de Kolmogorov-Smirnov.

Muestra el código R para la validación cruzada Kolmogorov-Smirnov

Los resultados aparecen en la Figura 6.12 donde el eje horizontal es Fold=1. Este proceso se repite para los otros siete folds. Los resultados se resumen en la Figura 6.12 y se aprecia que la Pareto es una distribución más confiable que la gamma.

# Representación de los estadísticos
matplot(1:k,t(cvalvec),type="b", col=c(1,3), lty=1:2, 
        ylim=c(0,0.4), pch = 0, xlab="Fold", ylab="KS Statistic")
legend("left", c("Pareto", "Gamma"), col=c(1,3),lty=1:2, bty="n")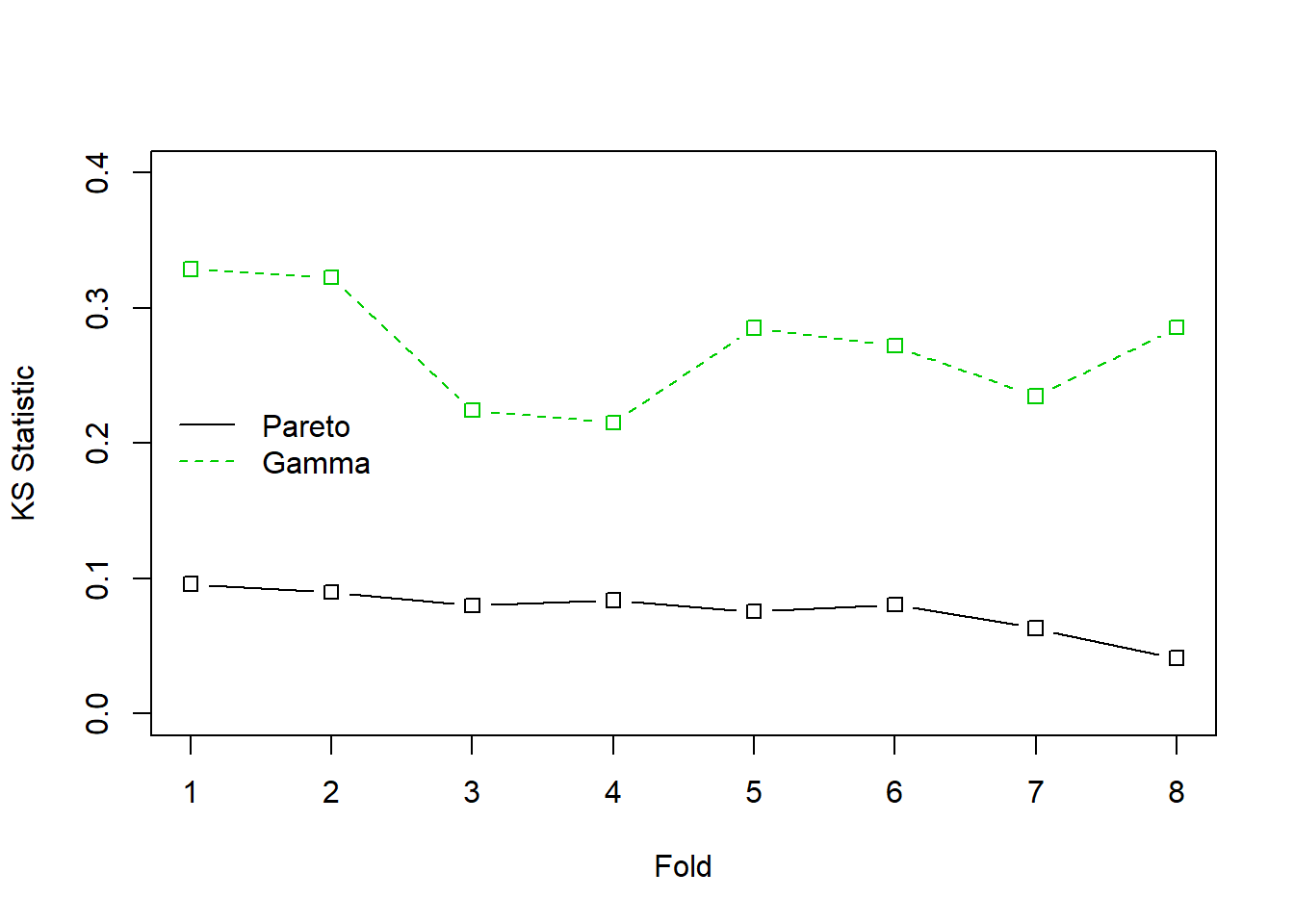
Estadísticos de Kolmogorov-Smirnov (KS) con validación cruzada para los datos de siniestros del fondo de propiedad. La línea continua negra corresponde a la distribución de Pareto, la línea verde discontinua corresponde a la gamma. El estadístico KS mide la mayor desviación entre la distribución ajustada y la empírica para cada uno de los 8 grupos, o folds, de los datos seleccionados aleatoriamente.

Figure 6.12: Estadísticos de Kolmogorov-Smirnov (KS) con validación cruzada para los datos de siniestros del fondo de propiedad. La línea continua negra corresponde a la distribución de Pareto, la línea verde discontinua corresponde a la gamma. El estadístico KS mide la mayor desviación entre la distribución ajustada y la empírica para cada uno de los 8 grupos, o folds, de los datos seleccionados aleatoriamente.

6.3.2 Validación cruzada dejando uno fuera

El caso especial donde \(k=n\) es conocido como validación cruzada dejando uno fuera. Este caso tiene importancia históricamente y está muy relacionado con los estadísticos jackknife, un precursor de la técnica bootstrap.

A pesar de que se presenta como un caso especial de validación cruzada, es conveniente dar una definición explícita. Se considera un estadístico genérico \(\widehat{\theta}=t(\boldsymbol{x})\) que es un estimador del parámetro de interés \(\theta\). La idea de jackknife es calcular \(n\) valores \(\widehat{\theta}_{-i}=t(\boldsymbol{x}_{-i})\), donde \(\boldsymbol{x}_{-i}\) es una submuestra de \(\boldsymbol{x}\) con el \(i\)-ésimo valor eliminado. La media de esos valores se denota como

\[ \overline{\widehat{\theta}}_{(\cdot)}=\frac{1}{n}\sum_{i=1}^n \widehat{\theta}_{-i} . \] Esos valores pueden usarse para crear estimaciones del sesgo del estadístico \(\widehat{\theta}\)

\[\begin{equation} Bias_{jack} = (n-1) \left(\overline{\widehat{\theta}}_{(\cdot)} - \widehat{\theta}\right) \tag{6.3} \end{equation}\]

así como de una estimación de la desviación estándar

\[\begin{equation} s_{jack} =\sqrt{\frac{n-1}{n}\sum_{i=1}^n \left(\widehat{\theta}_{-i} -\overline{\widehat{\theta}}_{(\cdot)}\right)^2} ~. \tag{6.4} \end{equation}\]

Ejemplo 6.3.2. Coeficiente de variación. A modo de ilustración, se considera una muestra pequeña ficticia \(\boldsymbol{x}=\{x_1,\ldots,x_n\}\) con realizaciones

sample_x <- c(2.46,2.80,3.28,3.86,2.85,3.67,3.37,3.40,
              5.22,2.55,2.79,4.50,3.37,2.88,1.44,2.56,2.00,2.07,2.19,1.77)

Se desea determinar el coeficiente de variación \(\theta = CV = \sqrt{\mathrm{Var~}X}/\mathrm{E~}X\).

Con esta base de datos, el estimador del coeficiente de variación resulta ser 0.31196. Pero, ¿cómo de fiable es este resultado? Para contestar a esta pregunta, se pueden calcular las estimaciones de jackknife del sesgo y su desviación estándar. El siguiente código muestra el estimador jackknife del sesgo es \(Bias_{jack} =\) -0.00627 y la desviación típica jackknife es \(s_{jack} =\) 0.01293.

CVar <- function(x) sqrt(var(x))/mean(x)
JackCVar <- function(i) sqrt(var(sample_x[-i]))/mean(sample_x[-i])
JackTheta <- Vectorize(JackCVar)(1:length(sample_x))
BiasJack <- (length(sample_x)-1)*(mean(JackTheta) - CVar(sample_x))
sd(JackTheta)

Ejemplo 6.3.3. Siniestros con daños corporales y ratios de eliminación de pérdida. En el Ejemplo 6.2.1, se mostró como calcular estimaciones bootstrap del sesgo y desviación estándar para la ratio de eliminación de pérdidas usando los datos de siniestros con daños corporales del Ejemplo 4.1.11. Se continúa ahora proporcionando cuantías comparables usando los estadísticos jackknife.

Tabla 6.7 resume los resultados de la estimación jackknife. Muestra como la estimación jackknife del sesgo y la desviación estándar de la ratio de eliminación \(\mathrm{E}~\min(X,d)/\mathrm{E}~X\) son ampliamente consistentes con la metodología bootstrap. Es más, se pueden usar las desviaciones estándar para construir intervalos de confianza basados en la normal, centrados alrededor del estimador corregido por el sesgo. Por ejemplo, para \(d=14000\), se vio en el Ejemplo 4.1.11 que el estimador no paramétrico de LER es 0.97678. Tiene un sesgo estimado de 0.00010, y resulta un estimador (jackknife) corregido por el sesgo igual a 0.97688. Los intervalos de confianza al 95% se obtienen creando un intervalo de dos veces la longitud de 1.96 desviaciones estándar jackknife, centrado sobre el estimador corregido por el sesgo (1.96 es aproximadamente el cuantil 97.5 de la distribución normal estándar).

Se muestra el código R

Table 6.7. Estimaciones Jackknife del LER en las franquicias seleccionadas
d Estimación NP Sesgo Bootstrap Bootstrap SD Sesgo Jackknife Jackknife SD Límite inferior del 95% Jackknife CI Límite superior del 95% Jackknife CI
4000 0.54113 0.00011 0.01237 0.00031 0.00061 0.53993 0.54233
5000 0.64960 0.00027 0.01412 0.00033 0.00068 0.64825 0.65094
10500 0.93563 0.00004 0.01017 0.00019 0.00053 0.93460 0.93667
11500 0.95281 -0.00003 0.00941 0.00016 0.00047 0.95189 0.95373
14000 0.97678 0.00016 0.00687 0.00010 0.00034 0.97612 0.97745
18500 0.99382 0.00014 0.00331 0.00003 0.00017 0.99350 0.99415

Discusión. Una de las cosas más interesantes sobre el caso especial de validación cruzada dejando uno fuera es la habilidad de replicar estimaciones de manera exacta. Es decir, cuando el tamaño del grupo o fold es solo uno, entonces no hay incertidumbre adicional inducida por la validación cruzada. Esto significa que los analistas pueden replicar de manera exacta el trabajo de otro, lo cual es una importante consideración.

Los estadísticos Jackknife fueron desarrollados para entender la precisión de estimadores, produciendo estimadores de sesgo y desviación estándar en las ecuaciones (6.3) y (6.4). Esto tiene que ver con algunas metas que se han asociado con las técnicas de bootstrap, no con métodos de validación cruzada. Esto demuestra como las técnicas estadísticas pueden usarse para alcanzar diferentes metas.

6.3.3 Validación cruzada y Bootstrap

El bootstrap es útil para proporcionar estimadores de la precisión, o variabilidad, de los estadísticos. También puede ser útil para la validación de modelos. El enfoque bootstrap para la validación de modelos es similar al enfoque dejando uno fuera y los procedimientos de validación k fold:

  • Se crea una muestra de bootstrap a través del remuestreo (con reemplazamiento) \(n\) índices en \(\{1,\cdots,n\}\). Esta será la muestra de entrenamiento. Se estima el modelo considerado en base a esta muestra.
  • La muestra de prueba, o muestra de validación, consiste en esas observaciones no seleccionadas para en entrenamiento. Se evalúa el modelo ajustado (basado en los datos de entrenamiento) usando los datos de prueba.

Este proceso se repite muchas (digamos \(B\)) veces. Se toma la media de los resultados y se selecciona al modelo basado en el estadístico de evaluación promedio.

Ejemplo 6.3.4. Fondo de propiedad de Wisconsin. Se vuelve a considerar el ejemplo 6.3.1 donde se investiga el ajuste de unas distribuciones gamma y Pareto a los datos del fondo de propiedad. Nuevamente se compara el desempeño predictivo usando el estadístico de Kolmogorov-Smirnov pero esta vez usando el procedimiento bootstrap para partir los datos entre muestra de entrenamiento y prueba. A continuación, se muestra el código ilustrativo.

Muestra el código R para procedimientos de validación Bootstrap

Se ha realizado el muestreo usando \(B=\) 100 réplicas. El estadístico KS promedio de la distribución Pareto era 0.058, que puede compararse con el promedio para la distribución gamma, 0.262. Esto es consistente con los resultados anteriores y proporciona una evidencia más de que el modelo Pareto es mejor para estos datos que el gamma.

6.4 Importance Sampling

En la Sección 6.1 se introducen las técnicas de Monte Carlo usando la técnica de la inversa: generar una variable aleatoria \(X\) con distribución \(F\), aplicar \(F^{-1}\) para llamar a un generador aleatorio (uniforme en el intervalo unitario). ¿Qué pasa si queremos realizar extracciones de acuerdo con \(X\), condicionado a \(X\in[a,b]\) ?

Se puede usar un mecanismo de aceptación-rechazo : extraer \(x\) de la distribución \(F\)

  • si \(x\in[a,b]\) : se mantiene (“aceptación”)
  • si \(x\notin[a,b]\) : se extrae otro (“rechazo”)

Se observa que de \(n\) valores inicialmente generados, se mantienen sólo \([F(b)-F(a)]\cdot n\) extracciones, en promedio.

Ejemplo 6.4.1. Extracciones de una distribución Normal.
Supongamos que se realizan extracciones de una distribución normal con media 2.5 y varianza 1, \(N(2.5,1)\), pero sólo se tiene interés en extracciones en extracciones mayores que \(a \ge 2\) y menores que \(b \le 4\). Es decir, se puede usar sólo una proporción de extracciones igual a \(F(4)-F(2) = \Phi(4-2.5)-\Phi(2-2.5)\) = 0.9332 - 0.3085 = 0.6247. La Figura 6.13 demuestra que algunas extracciones caen en el intervalo \((2,4)\) y otras están fuera.

Muestra el código R para el mecanismo de aceptación-rechazo 
for (i in 1:numAnimation) {pic_ani()}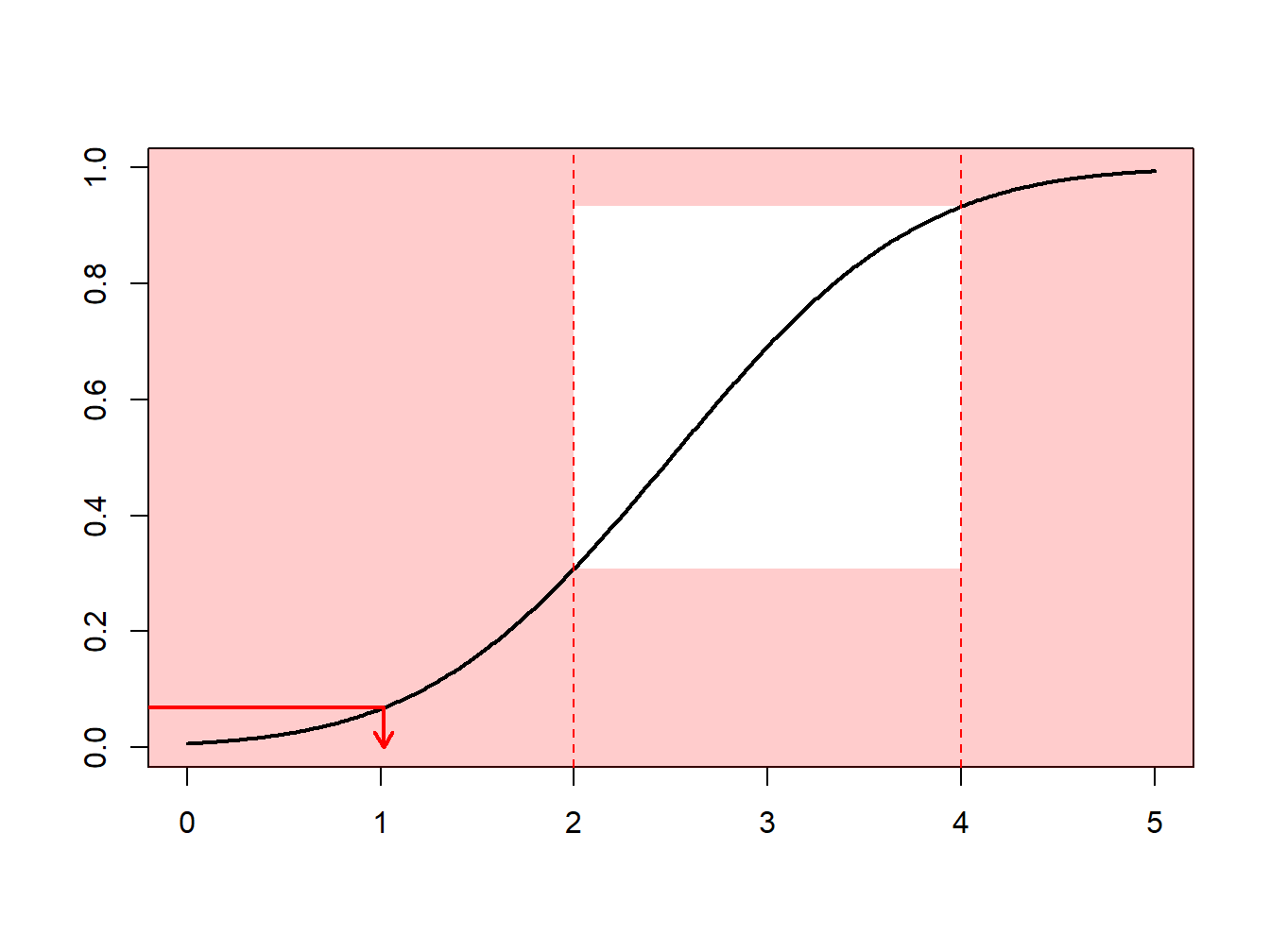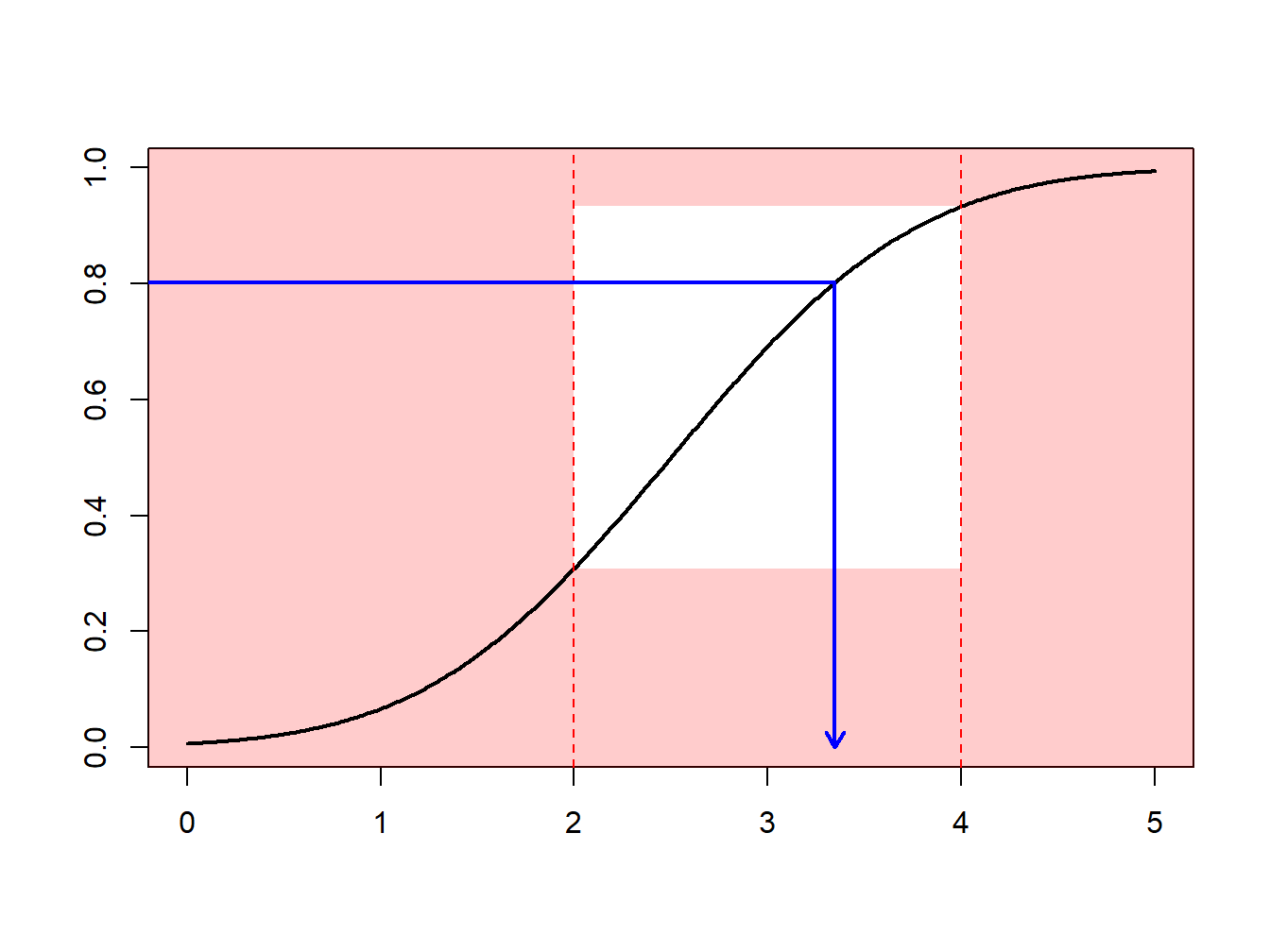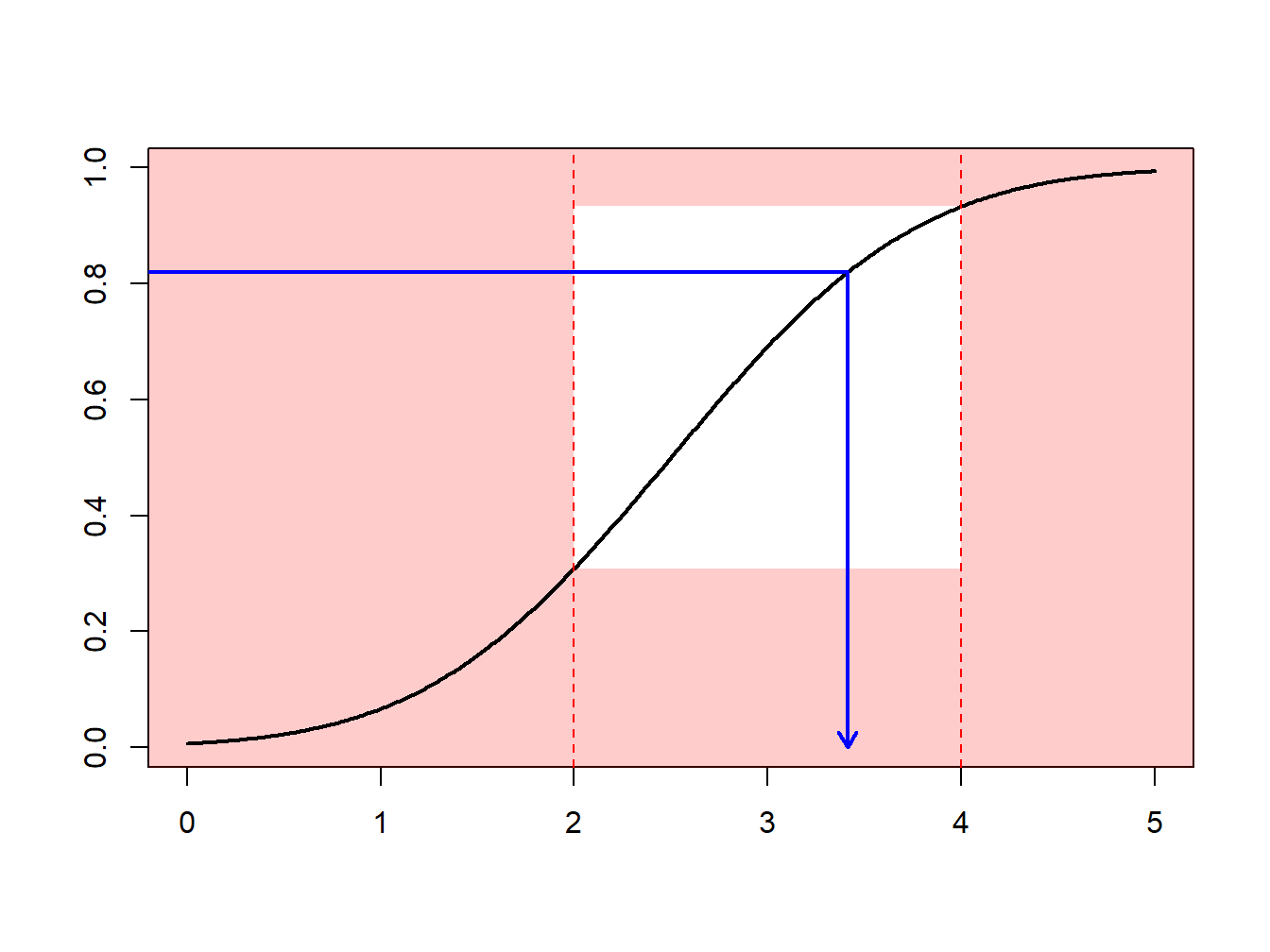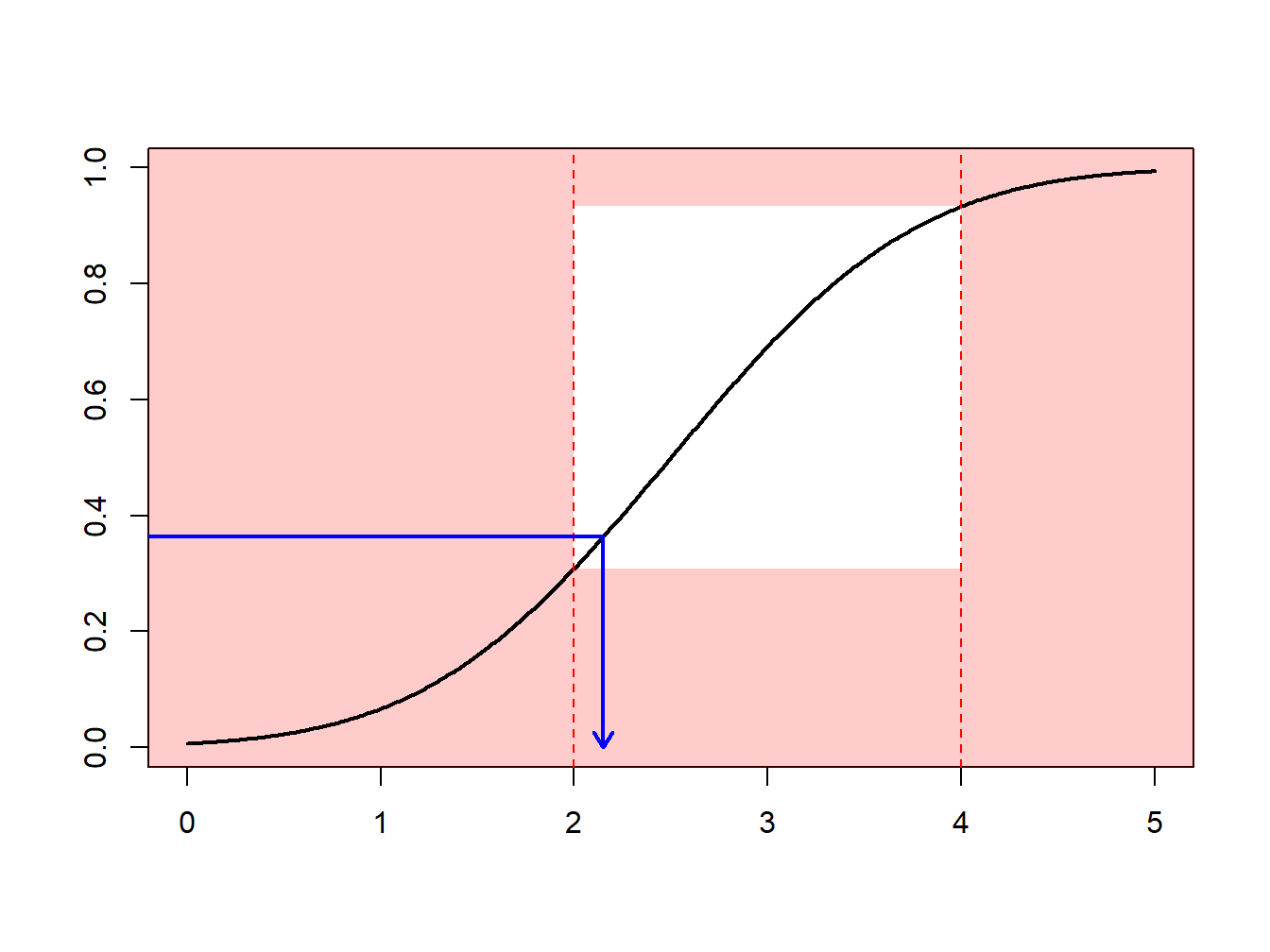
Demostración animada de extracciones dentro y fuera de (2,4)

Figure 6.13: Demostración animada de extracciones dentro y fuera de (2,4)

En su lugar, se pueden realizar extracciones de acuerdo con la distribución condicional \(F^{\star}\) definida como

\[ F^{\star}(x) = \Pr(X \le x | a < X \le b) =\frac{F(x)-F(a)}{F(b)-F(a)}, \ \ \ \text{for } a < x \le b . \] Usando el método de la transformada inversa de la Sección 6.1.2, se tiene que la extracción

\[ X^\star=F^{\star-1}\left( U \right) = F^{-1}\left(F(a)+U\cdot[F(b)-F(a)]\right) \] tiene distribución \(F^{\star}\). Expresado de otra forma, se define

\[ \tilde{U} = (1-U)\cdot F(a)+U\cdot F(b) \] y entonces se usa \(F^{-1}(\tilde{U})\). Con este enfoque, cada extracción cuenta.

Esto puede estar relacionado con la importancia del mecanismo de muestreo : se realizan extracciones más frecuentemente en regiones donde se espera tener cantidades que tienen algún interés. Esta transformación puede ser considerada como “un cambio de medida.”

Muestra el código R para la importancia del muestreo por el método de la transformada inversa 
for (i in 1:numAnimation) {pic_ani()}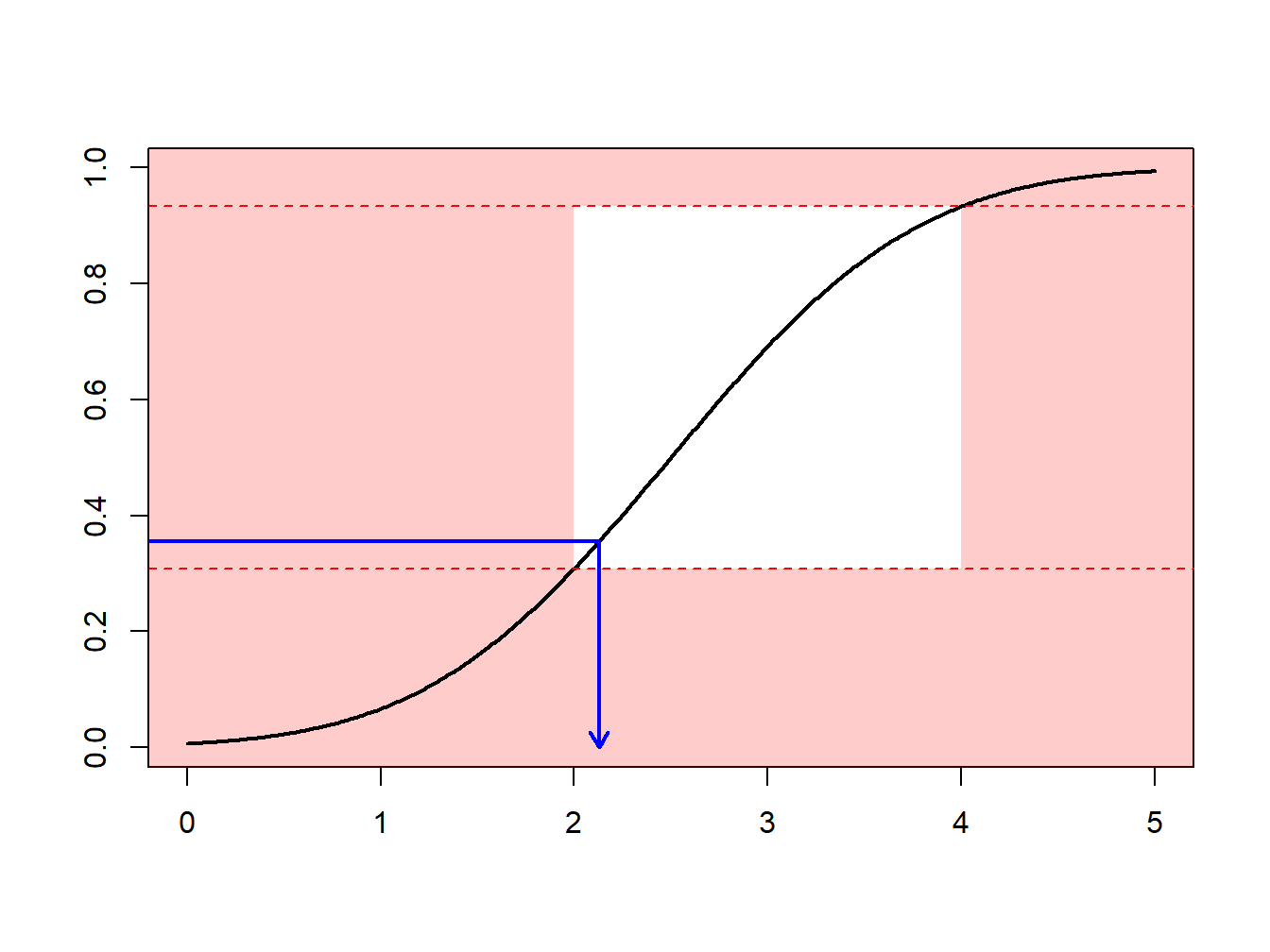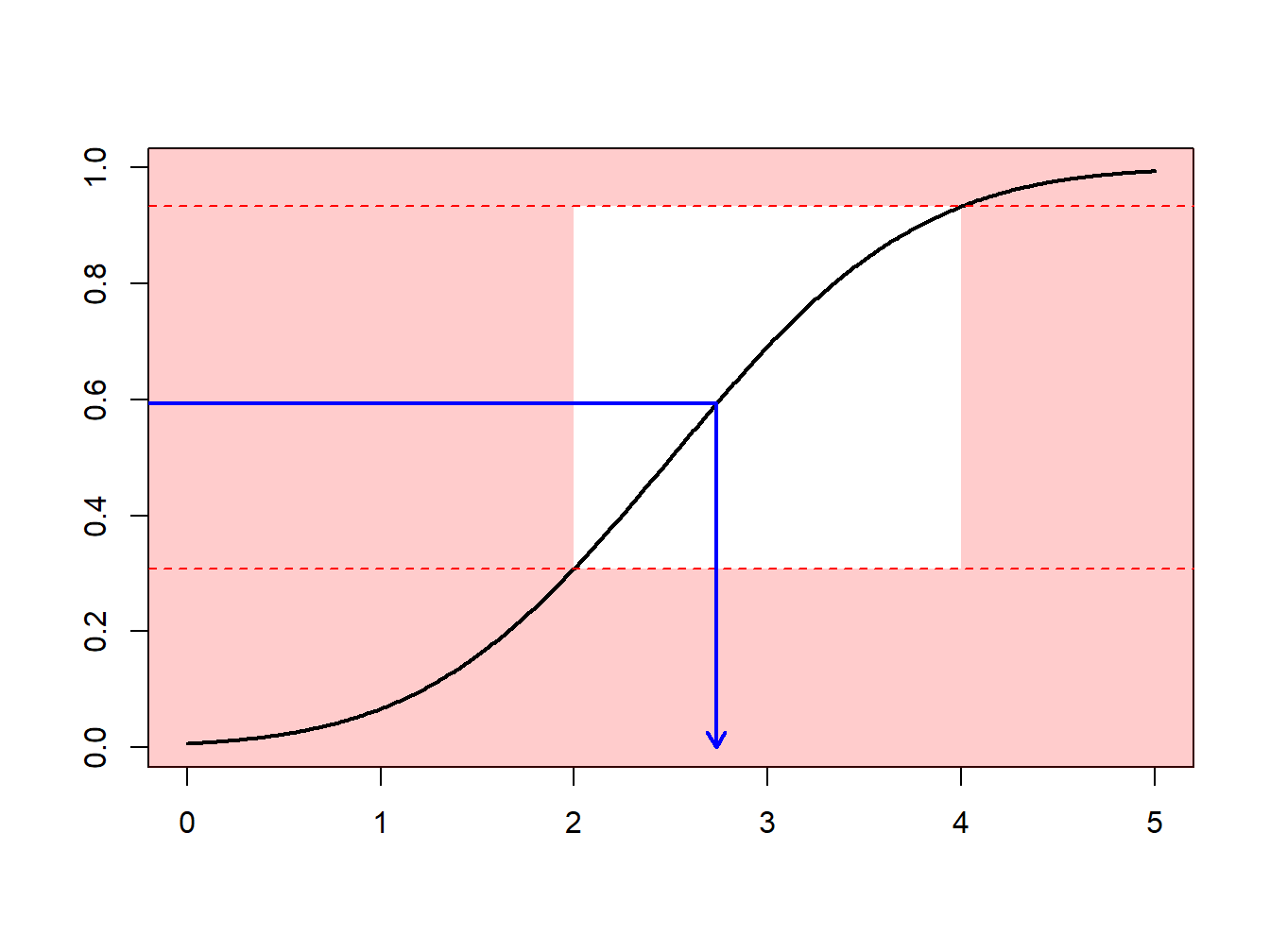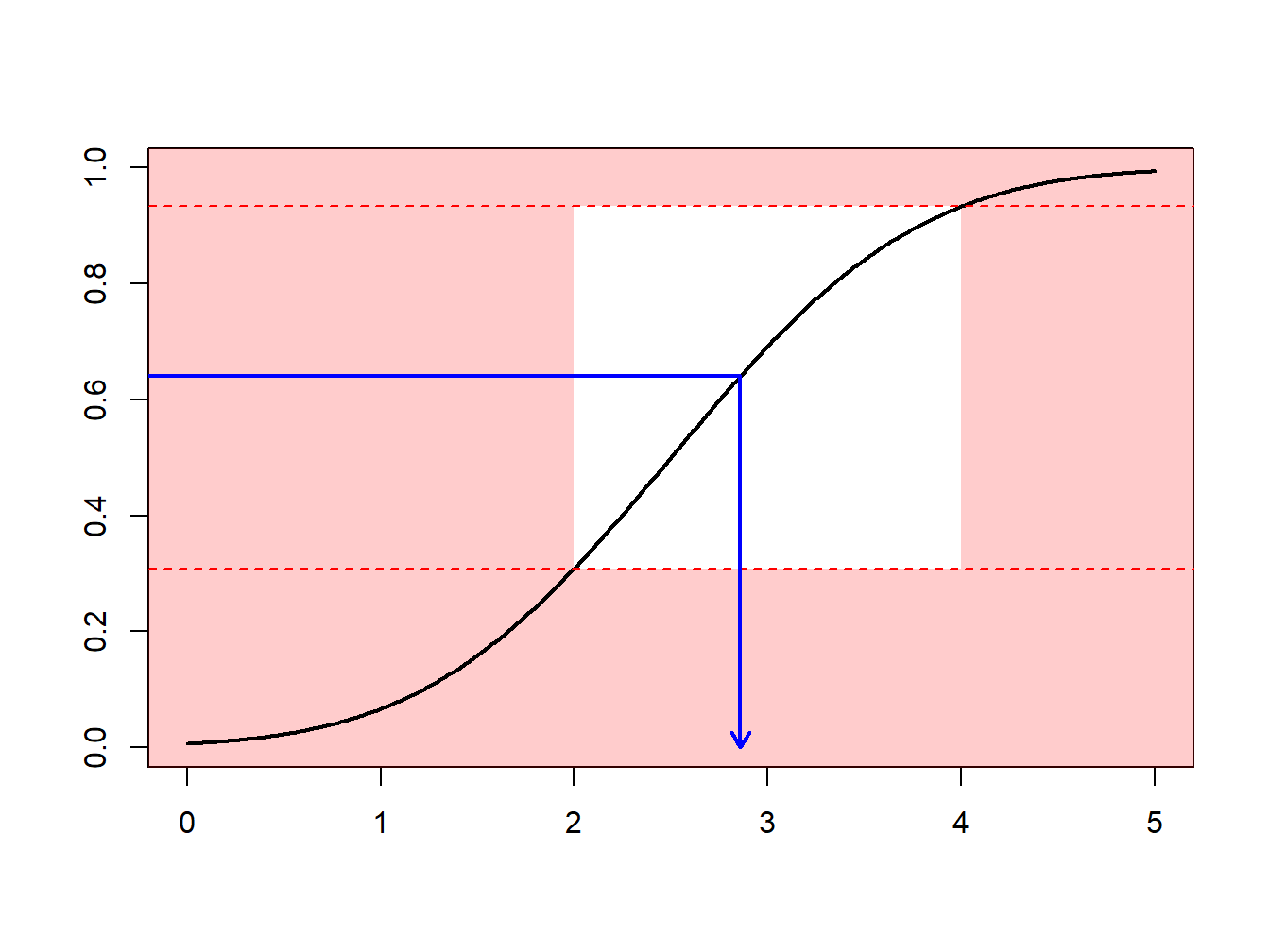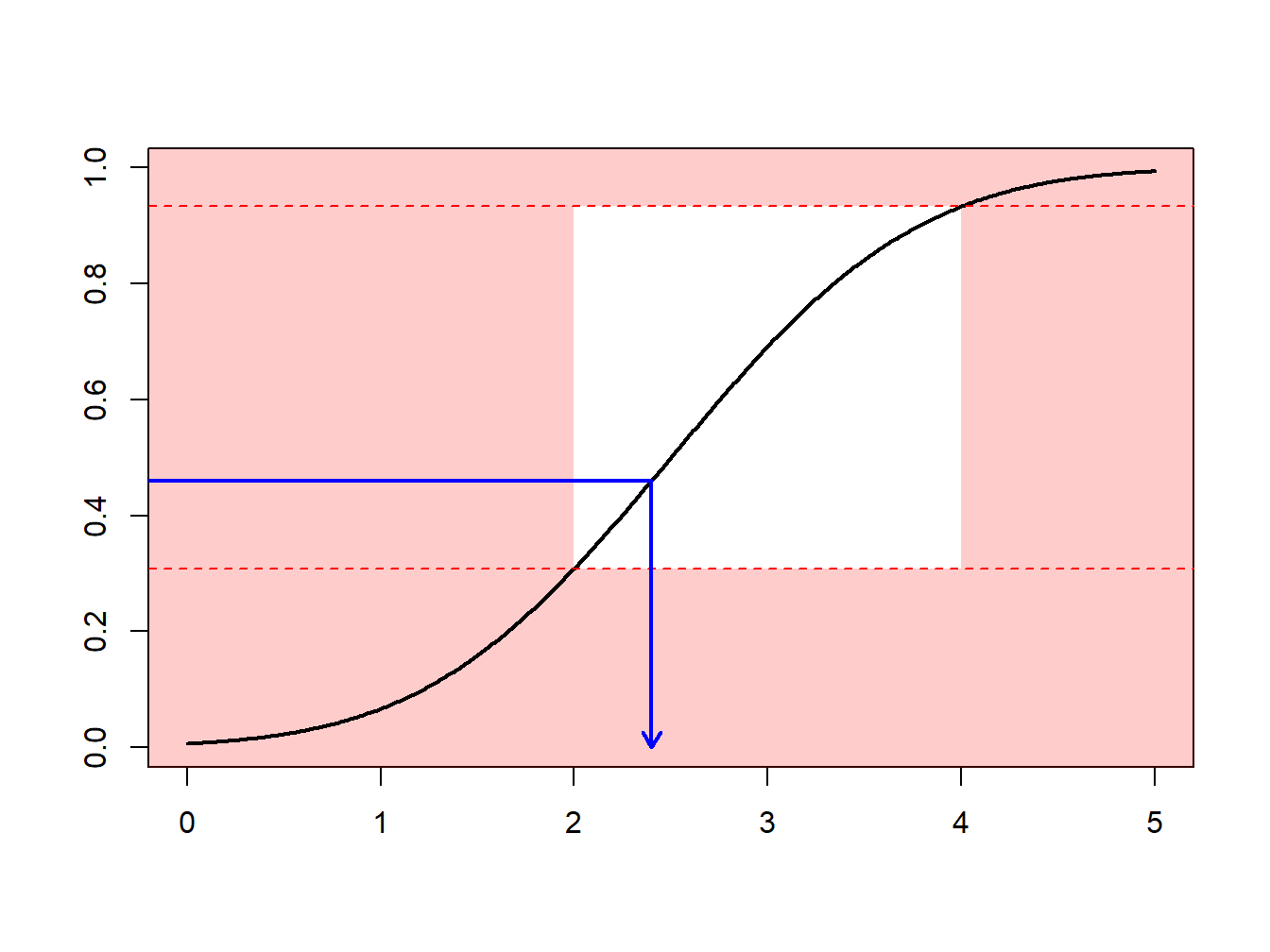

En el Ejemplo 6.4.1., la inversa de la distribución normal está disponible fácilmente (en R, la función es qnorm). Sin embargo, para otras aplicaciones, este no es el caso. Entonces, simplemente se usan métodos numéricos para determinar \(X^\star\) como la solución de la ecuación \(F(X^\star) =\tilde{U}\) donde \(\tilde{U}=(1-U)\cdot F(a)+U\cdot F(b)\). Véase el siguiente código ilustrativo.

Muestra el código R para la importancia del muestreo via soluciones numéricas 
for (i in 1:numAnimation) {pic_ani()}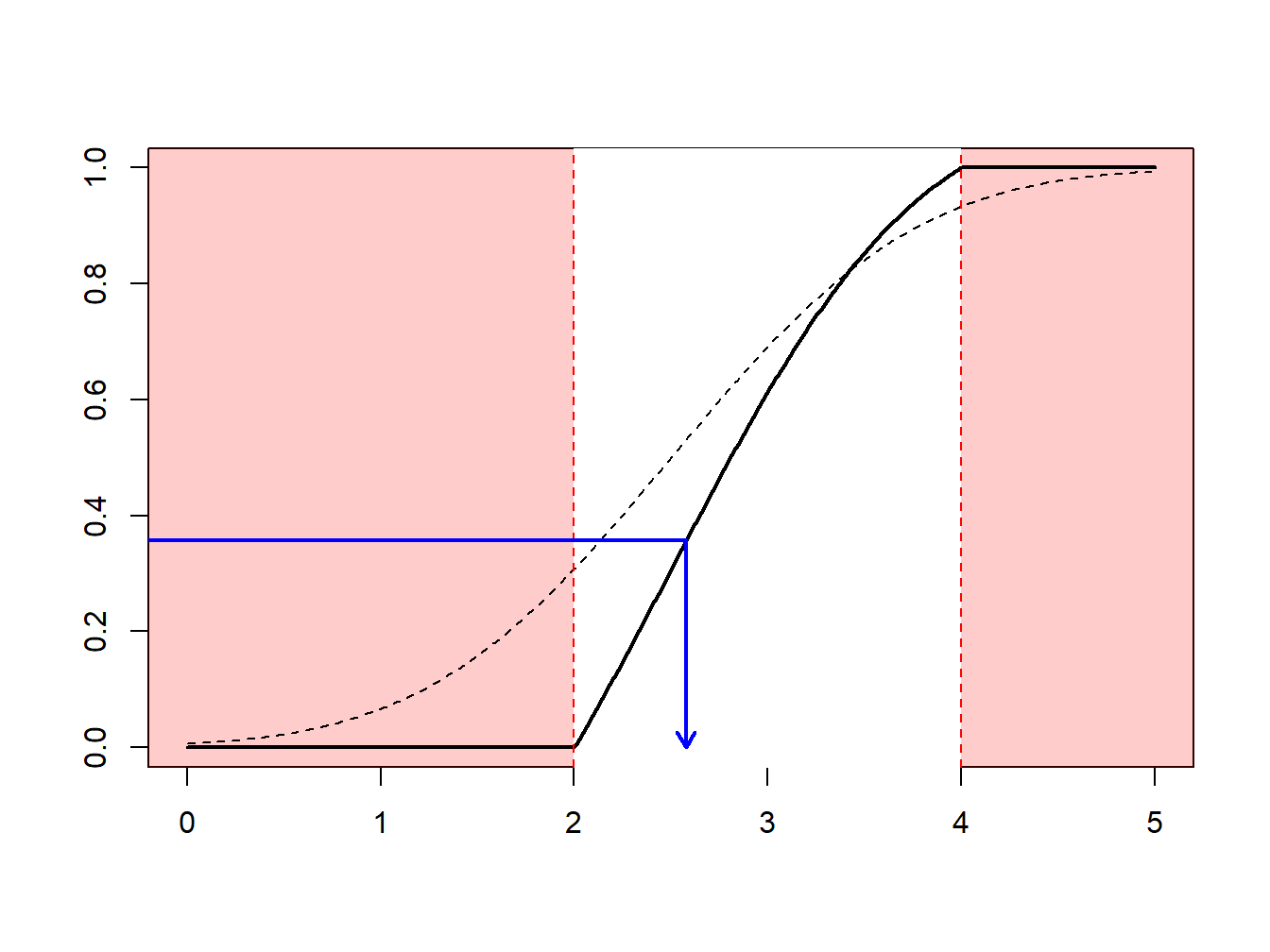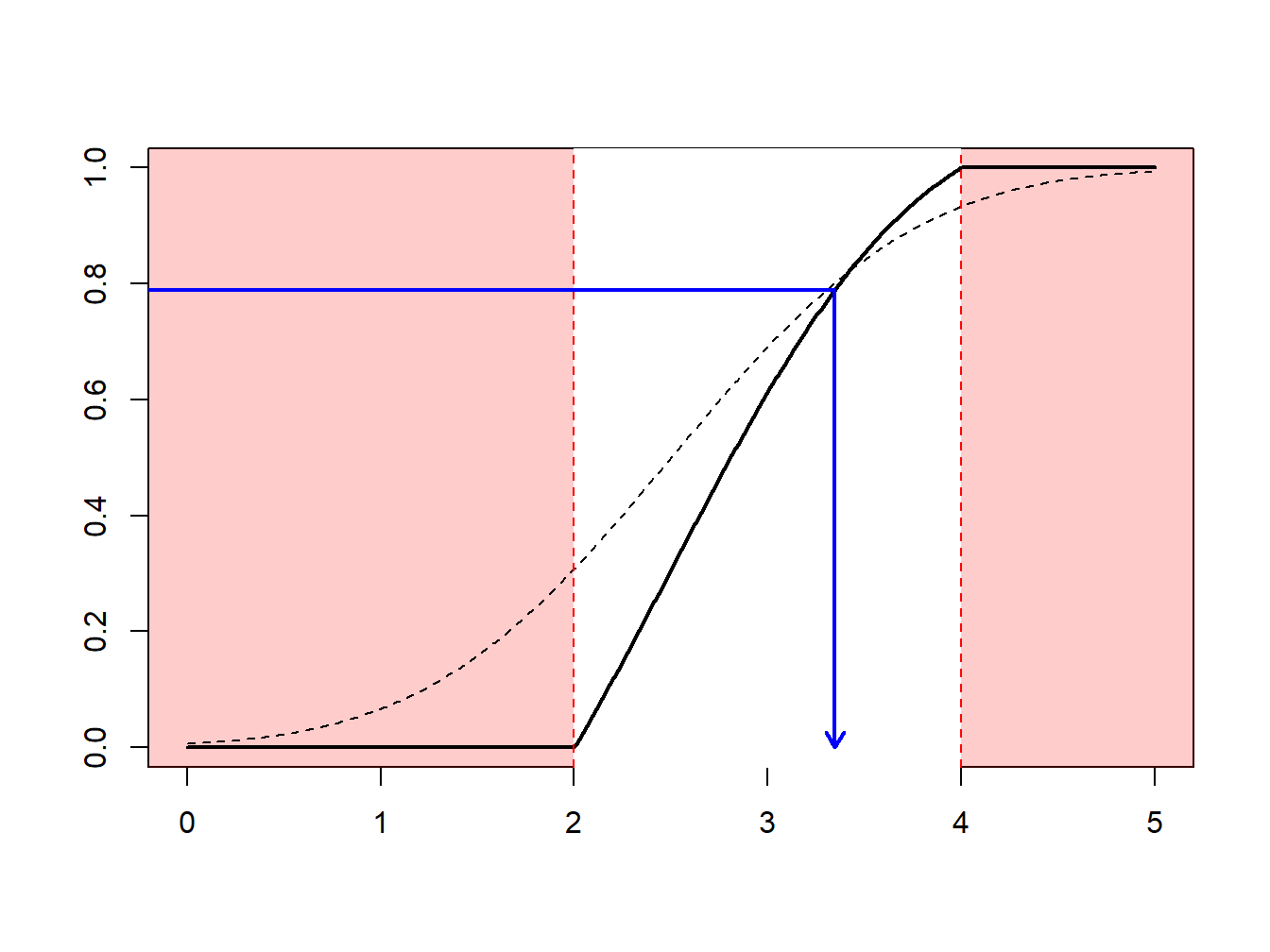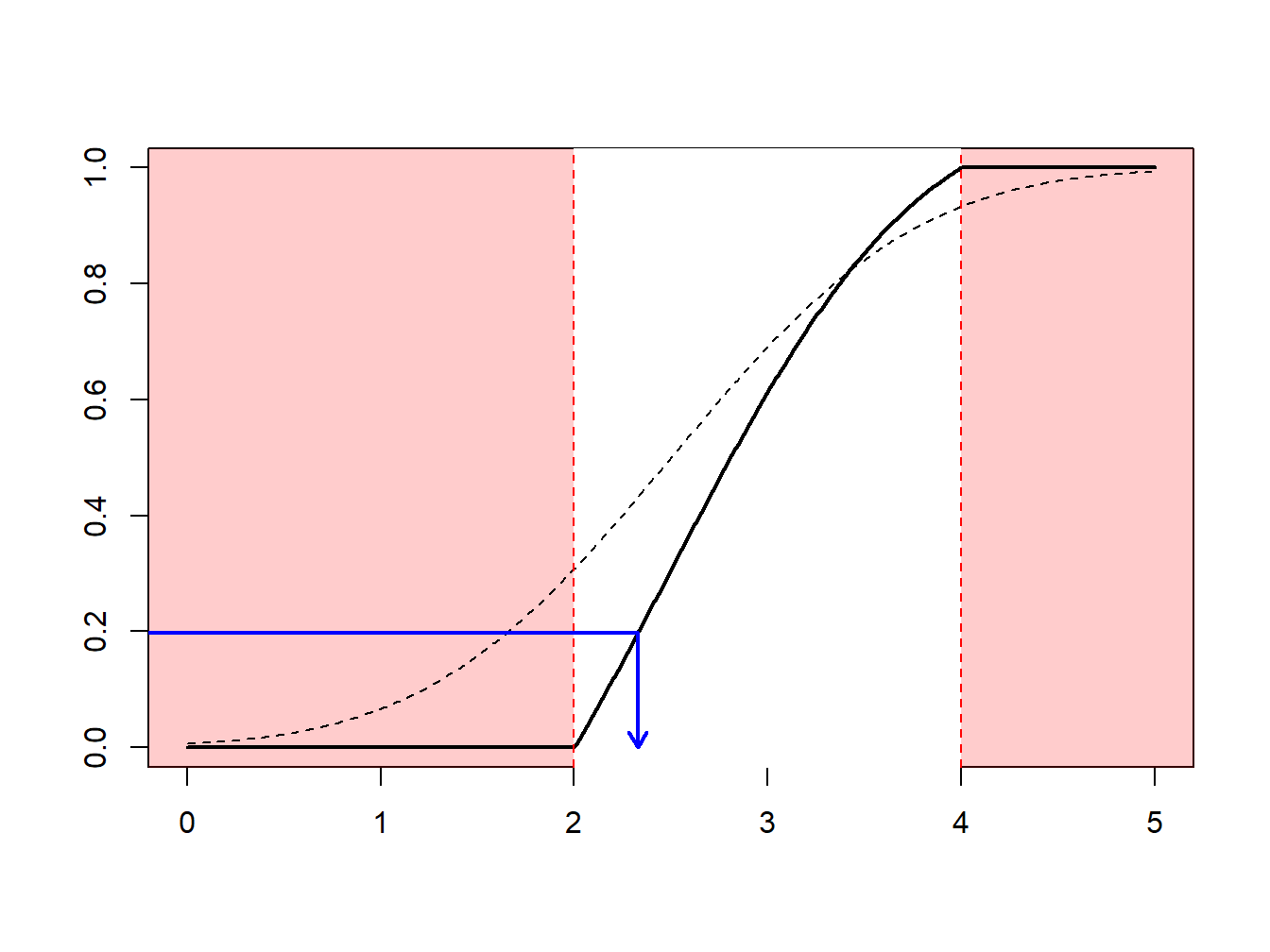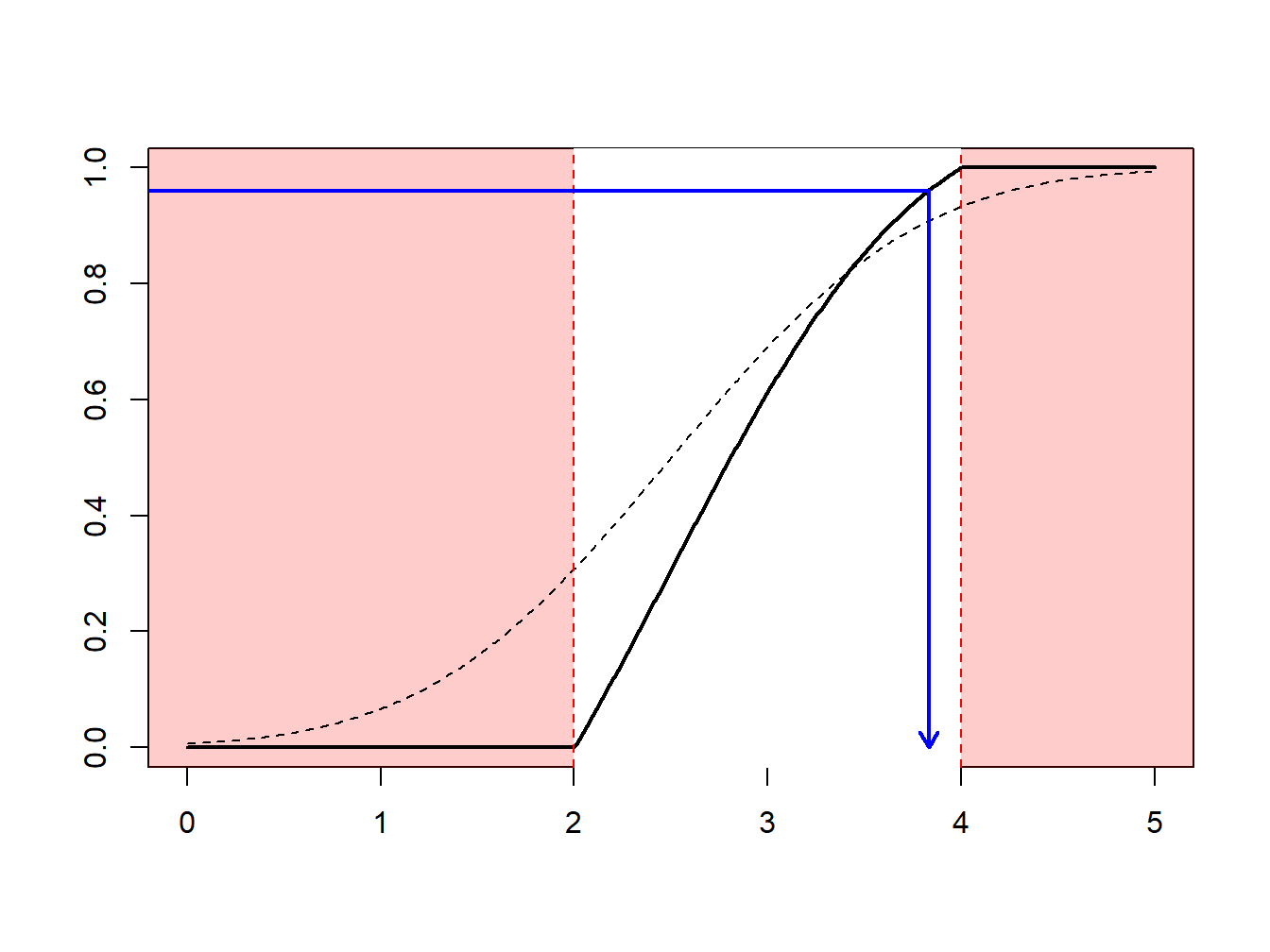

6.5 Monte Carlo Markov Chain (MCMC)

Esta sección se está escribiendo y no está complete ni editada. El contenido que se muestra es para haceros una idea de lo que contendrá la versión final.

La idea de las técnicas de Monte Carlo se basa en la ley de los grandes números (que asegura la convergencia de la media hacia la integral) y el teorema central del límite (que se usa para cuantificar la incertidumbre en los cálculos). Es necesario recordar que si \((X_i)\) es una secuencia i.id. de variables aleatorias con distribución \(F\), entonces

\[ \frac{1}{\sqrt{n}}\left(\sum_{i=1}^n h(X_i)-\int h(x)dF(x)\right)\overset{\mathcal{L}}{\rightarrow }\mathcal{N}(0,\sigma^2),\text{ as }n\rightarrow\infty. \] para alguna varianza \(\sigma^2>0\). Pero de hecho, el teorema ergódico se puede usar para rebajar el resultado anterior, dado que no es neceario tener independencia de las variables. Más concretamente, si \((X_i)\) es un proceso de Markov con medida invariante \(\mu\), bajo algunos supuestos técnicos adicionales, se puede obtener que

\[ \frac{1}{\sqrt{n}}\left(\sum_{i=1}^n h(X_i)-\int h(x)d\mu(x)\right)\overset{\mathcal{L}}{\rightarrow }\mathcal{N}(0,\sigma_\star^2),\text{ as }n\rightarrow\infty. \] para alguna varianza \(\sigma_\star^2>0\).

Por lo tanto, de esta propiedad, se puede ver que es posible no necesariamente generar valores independientes a partir de \(F\), sino también generar un proceso de markov con medida invariante \(F\), y considerar medias sobre el proceso (no necesariamente independiente). Se considera el caso de un vector Gausiano restringido: se desean generar parejas aleatorias de un vector aleatorio \(\boldsymbol{X}\), pero sólo interesa el caso en que la suma de los (‘composants’)` es suficientemente grande, lo que puede expresarse como \(\boldsymbol{X}^T\boldsymbol{1}> m\) para algún valor real \(m\). Por supuesto, es posible usar el algoritmo aceptación-rechazo, pero se ha vito que puede ser bastante ineficiente. Se puede usar el Hastings Metropolis y el muestreo de Gibbs para generar un proceso de Markov con esta medida invariante.

6.5.1 Hastings Metropolis

El algoritmo es bastante simple de generar a partir de \(f\): se comienza con un valor factible \(x_1\). Entonces, en el paso \(t\), se necesita especificar una transición núcleo: dado \(x_t\), se necesita la distribución condicional de \(X_{t+1}\) dado \(x_t\). El algoritmo funcionará bien si la distribución condicional se puede simular fácilmente. Sea \(\pi(\cdot|x_t)\) esta probabilidad. Se obtiene un valor potencial \(x_{t+1}^\star\), y \(u\), de una distribución uniforme. Se calcula

\[ R= \frac{f(x_{t+1}^\star)}{f(x_t)} \] y

  • si \(u < r\), entonces \(x_{t+1}=x_t^\star\)
  • si \(u\leq r\), entonces \(x_{t+1}=x_t\)

Aquí \(r\) se denomina ratio-aceptación: se acepta el nuevo valor con probabilidad \(r\) (o en realidad el menor entre \(1\) y \(r\) dado que \(r\) puede exceder \(1\)).

Por ejemplo, se asume que \(f(\cdot|x_t)\) es uniforme en \([x_t-\varepsilon,x_t+\varepsilon]\) para algún \(\varepsilon>0\), y donde \(f\) (la distribución objetivo) es la \(\mathcal{N}(0,1)\). Nunca se realizarán extracciones de \(f\), pero se usará para calcular la ratio de aceptación en cada paso.

Se muestra el código R

En el código de arriba, vec contiene los valores de \(\boldsymbol{x}=(x_1,x_2,\cdots)\), innov es la innovación.

Se muestra el código R 
for (k in 2:23) {pic_ani(k)}

Ahora, si se usan más simulaciones, se obtiene

vec <- metrop1(10000)
simx <- vec[1000:10000,1]
par(mfrow=c(1,4))
plot(simx,type="l")
hist(simx,probability = TRUE,col="light blue",border="white")
lines(u,dnorm(u),col="red")
qqnorm(simx)
acf(simx,lag=100,lwd=2,col="light blue")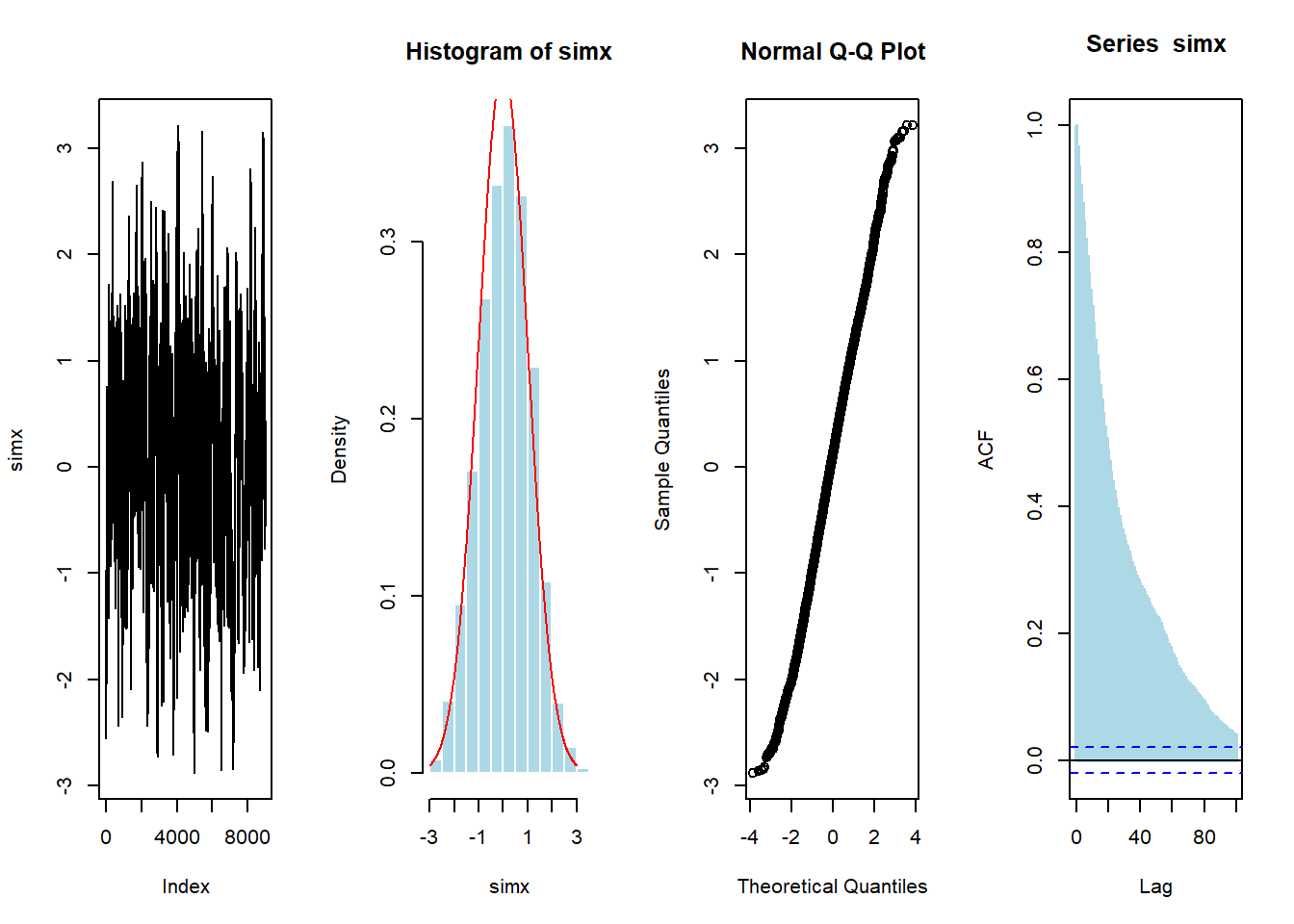

6.5.2 Muestreo de Gibbs

Se considera algún vector \(\boldsymbol{X}=(X_1,\cdots,X_d)\) con components independientes, \(X_i\sim\mathcal{E}(\lambda_i)\). Se realiza un muestro para muestrear de \(\boldsymbol{X}\) dado \(\boldsymbol{X}^T\boldsymbol{1}>s\) para algún umbral \(s>0\).

  • se comienza con algún valor inicial \(\boldsymbol{x}_0\) tal que
  • se elige (aleatoriamente) \(i\in\{1,\cdots,d\}\)
  • \(X_i\) dado que \(X_i > s-\boldsymbol{x}_{(-i)}^T\boldsymbol{1}\) tiene una distribucion Exponencial \(\mathcal{E}(\lambda_i)\)
  • se extrae \(Y\sim \mathcal{E}(\lambda_i)\) y se establece \(x_i=y +(s-\boldsymbol{x}_{(-i)}^T\boldsymbol{1})_+\) hasta que \(\boldsymbol{x}_{(-i)}^T\boldsymbol{1}+x_i>s\)
Se muestra el Código R 
plot(sim,xlim=c(1,11),ylim=c(0,4.3))
polygon(c(-1,-1,6),c(-1,6,-1),col="red",density=15,border=NA)
abline(5,-1,col="red")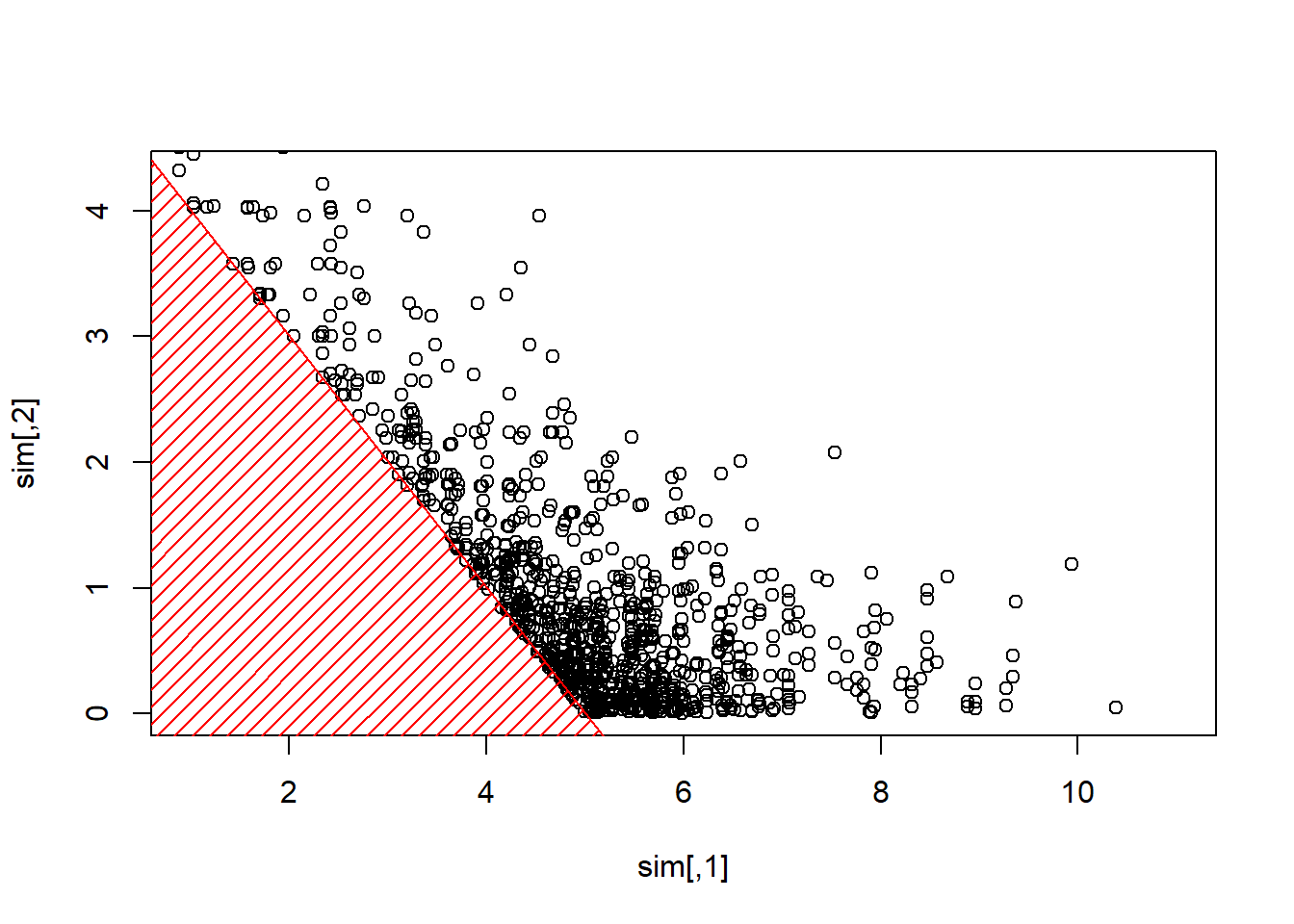

La construcción de la secuencia (los algoritmos MCMC son iterativos) puede visualizarse abajo

Se muestra el código R 
for (i in 2:100) {pic_ani(i)}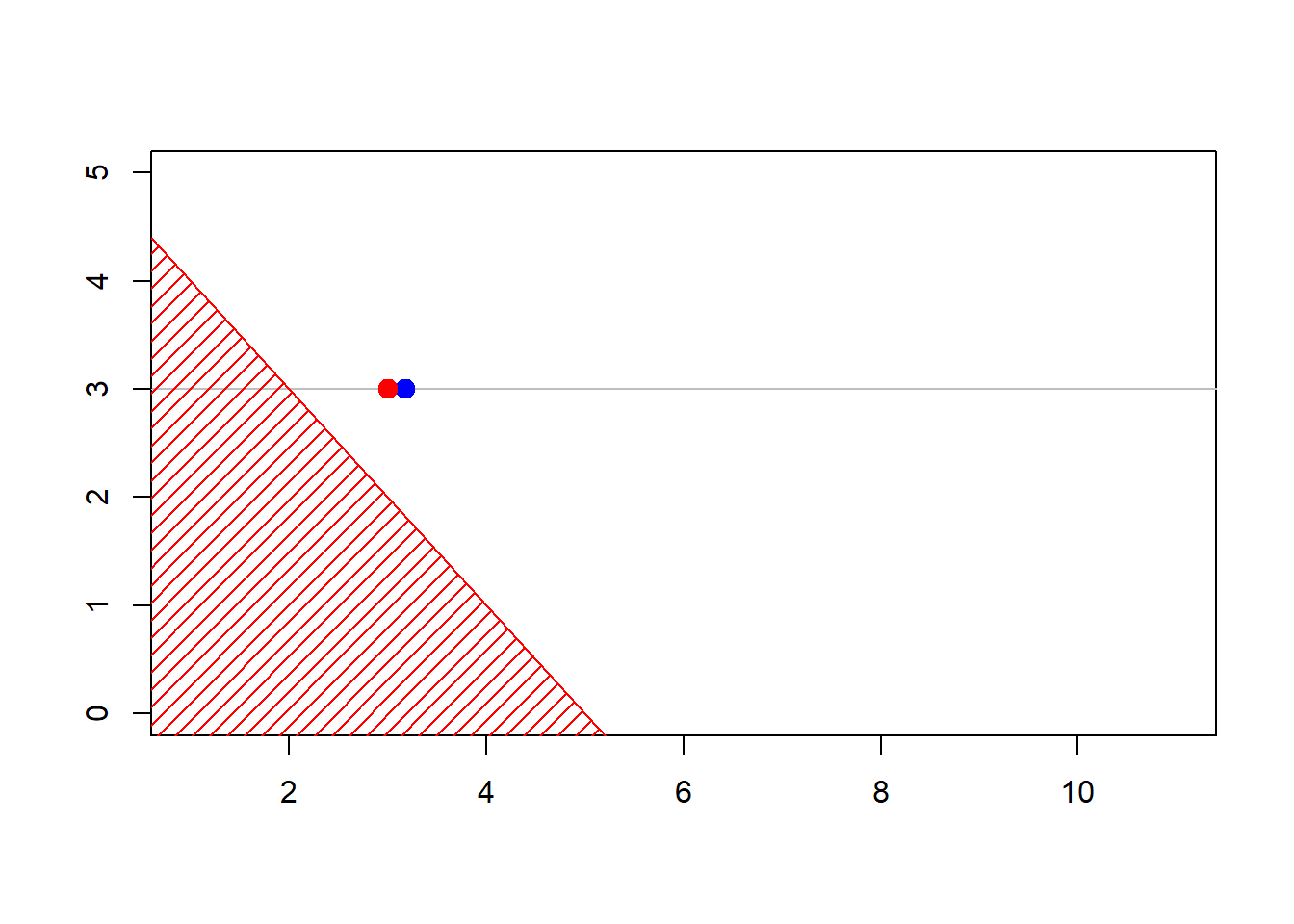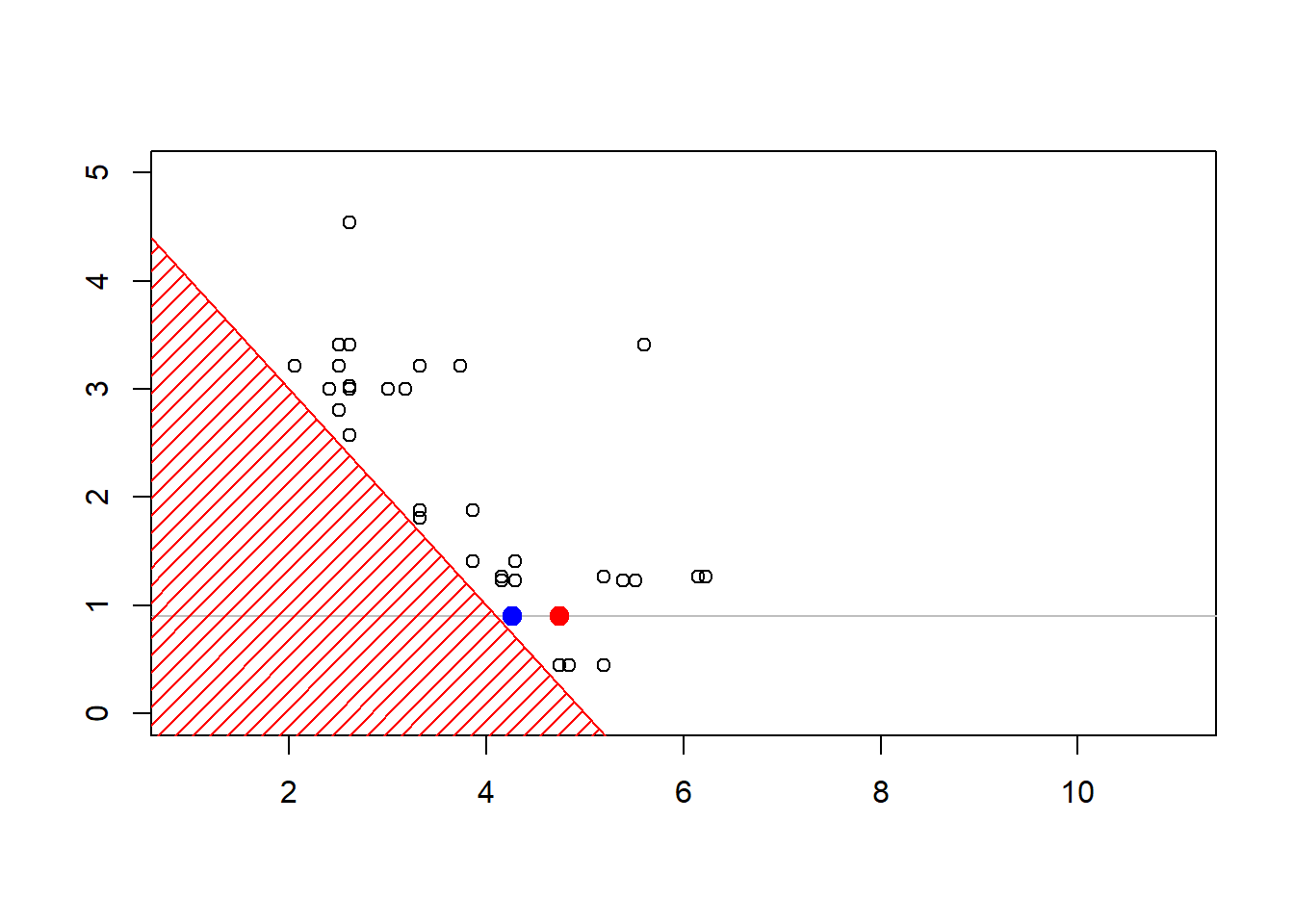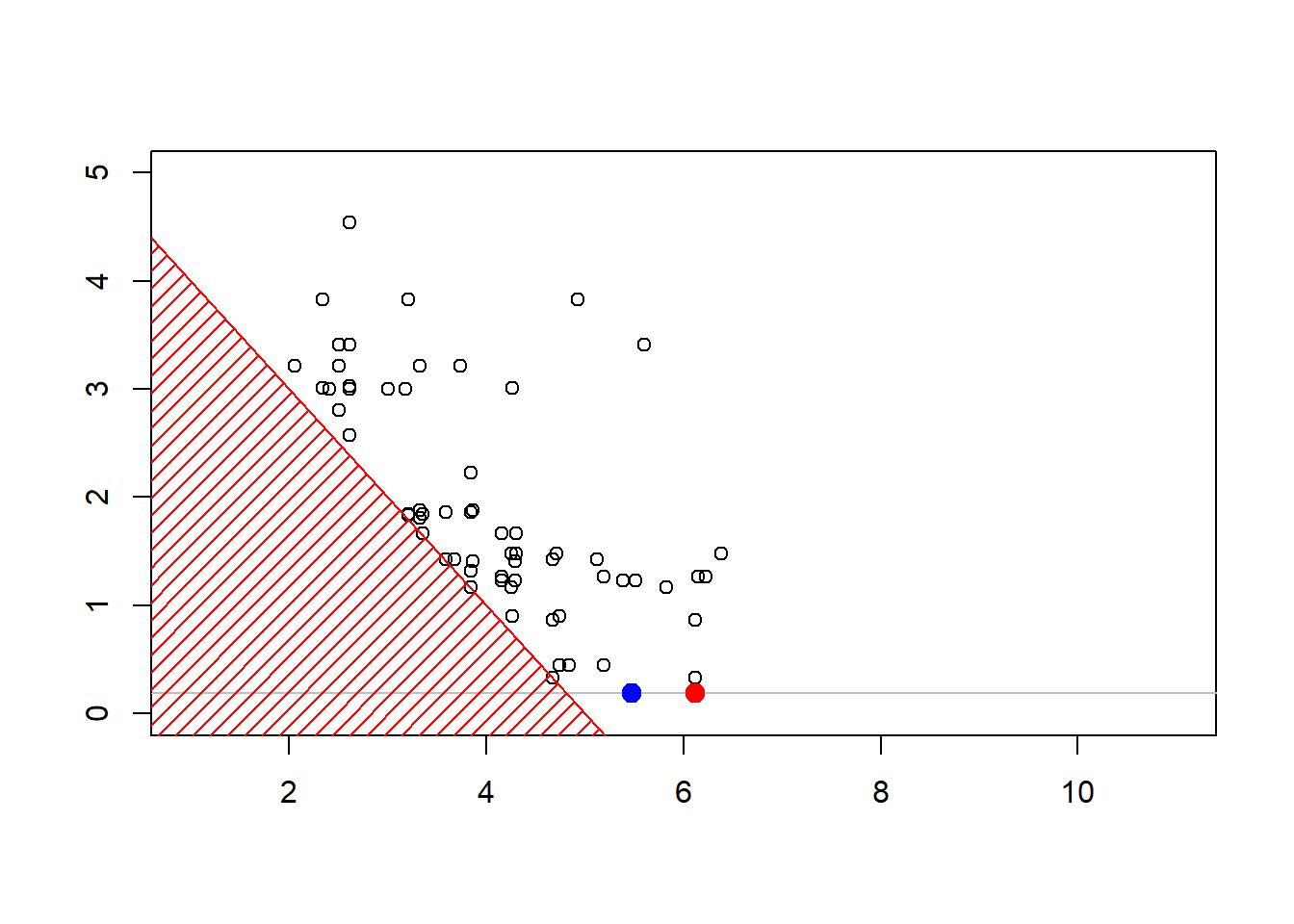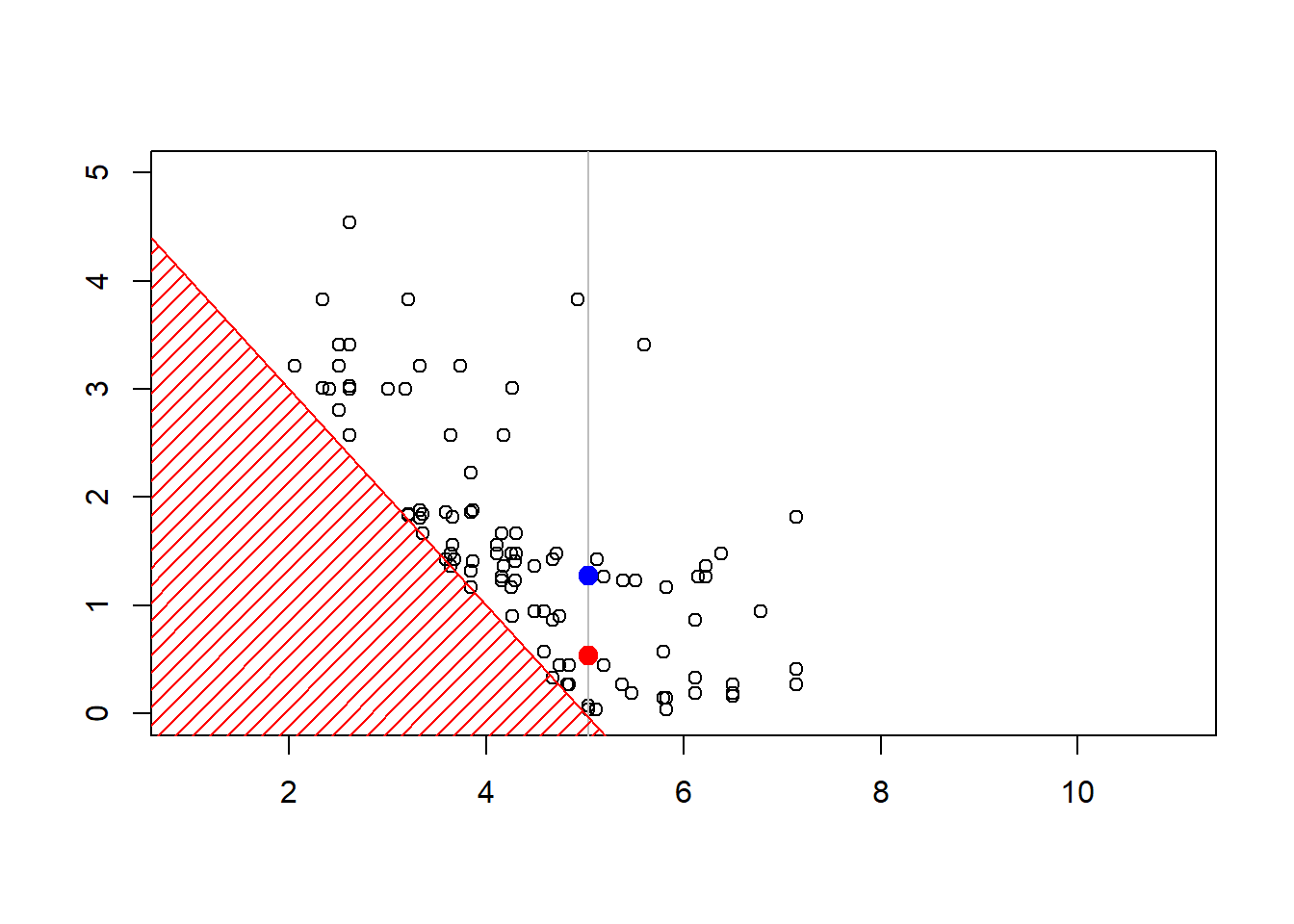

6.6 Recursos Adicionales y Colaboradores

Colaboradores

  • Arthur Charpentier, Université du Quebec á Montreal, y Edward W. (Jed) Frees, University of Wisconsin-Madison, son los principales autores de la versión inicial de este capítulo. Email: y/o para comentarios sobre este capítulo y sugerencias de mejora.
  • Revisores del capítulo: Escribir a Jed o Arthur; para añadir tu nombre aquí.
  • Traducción al español: Ana María Pérez-Marín (Universitat de Barcelona).

6.6.1 TS 6.A. Bootstrap Applications in Predictive Modeling

This section is being written.