Chapter 11 Provisiones
Vista Previa del Capítulo. Este capítulo introduce las provisiones (también conocidas como reservas por pérdidas) para seguros de propiedad y accidentes (P&C, según sus siglas en inglés, o generales, no-vida). En particular, el capítulo presenta algunas herramientas analíticas básicas esenciales para evaluar las reservas de una cartera de productos de seguros de P&C. En primer lugar, la Sección 11.1 motiva la necesidad de las provisiones. Después la Sección 11.2 estudia las fuentes de datos disponibles e introduce algunas notaciones formales para enfocar las provisiones como un desafío de predicción. A continuación, la sección 11.3 cubre el método de chain-ladder y el modelo de chain-ladder con distribución libre de Mack. La sección 11.4 finalmente desarrolla un enfoque totalmente estocástico para determinar la reserva pendiente con modelos lineales generalizados (GLMs, según sus siglas en inglés), incluyendo la técnica de bootstrapping para obtener una distribución predictiva de la reserva pendiente a través de la simulación.
11.1 Motivación
Nuestro punto de partida es la vida de un siniestro en un seguro de P&C. La figura 11.1 muestra el desarrollo del siniestro a lo largo del tiempo e identifica los eventos de interés:
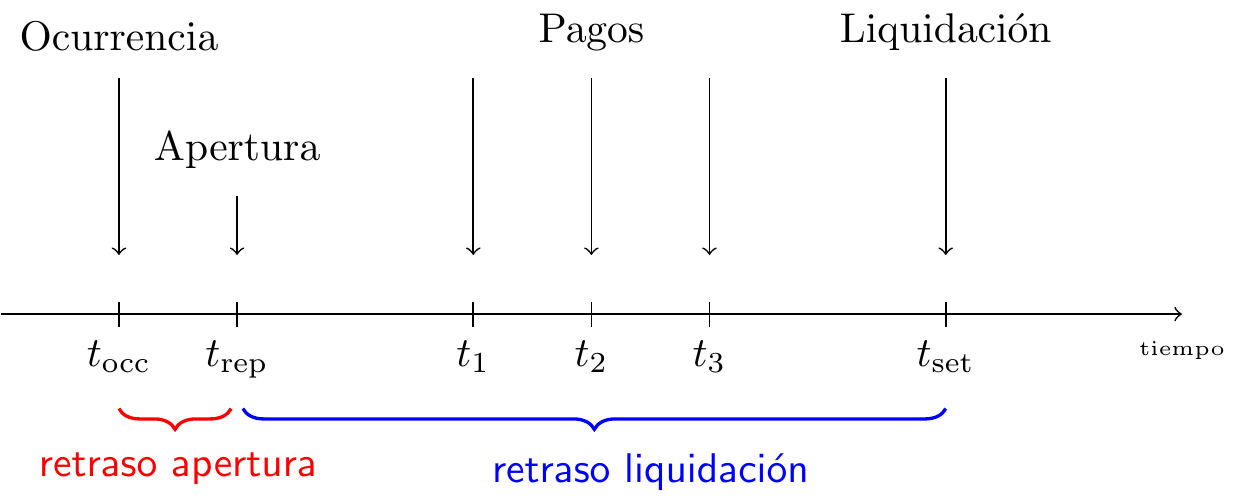
Figure 11.1: Vida o run-off de un siniestro
El evento asegurado o accidente ocurre en el momento \(t_{occ}\). Este siniestro es reportado a la compañía de seguros en el momento \(t_{rep}\), después de un cierto tiempo de demora. Si la compañía de seguros acepta la reclamación presentada, realizará diferentes pagos para reembolsar la pérdida financiera del titular de la póliza. En este ejemplo, la compañía de seguros compensa la pérdida sufrida con pagos por pérdidas en los momentos \(t_1\), \(t_2\) u \(t_3\). Finalmente, la reclamación se liquida o cierra en el momento \(t_{set}\).
A menudo las reclamaciones no se liquidan inmediatamente debido a la presencia de una demora en la presentación de la reclamación, un retraso en el proceso de liquidación o ambos. El retraso en la notificación es el tiempo que transcurre entre la ocurrencia del evento asegurado y la notificación de este evento a la compañía de seguros. El tiempo entre la notificación y la liquidación de una reclamación se conoce como la demora en la liquidación. Por ejemplo, es muy intuitivo que una reclamación por daños materiales se resuelve más rápidamente que una reclamación por lesiones corporales que impliquen un tipo de lesión compleja. Las reclamaciones cerradas pueden reabrirse debido a nuevos acontecimientos, por ejemplo, una lesión que requiere un tratamiento adicional. En conjunto, el desarrollo del siniestro requiere un tiempo. La presencia de este retraso en la tramitación de un siniestro obliga al asegurador a disponer de capital para liquidar estas reclamaciones en el futuro.
11.1.1 Siniestros cerrados, IBNR, y RBNS
Basándonos en el estado de la liquidación de la reclamación, distinguimos tres tipos de siniestros en los libros de una compañía de seguros. El primer tipo de siniestro es una reclamación cerrada. Para estos siniestros se ha observado el desarrollo completo. Con la línea roja de la figura 11.2 que indica el momento presente, todos los eventos del desarrollo del siniestro tienen lugar antes del momento presente. Por lo tanto, estos eventos se observan en el momento actual. Por comodidad, asumiremos que una reclamación cerrada no puede reabrirse.
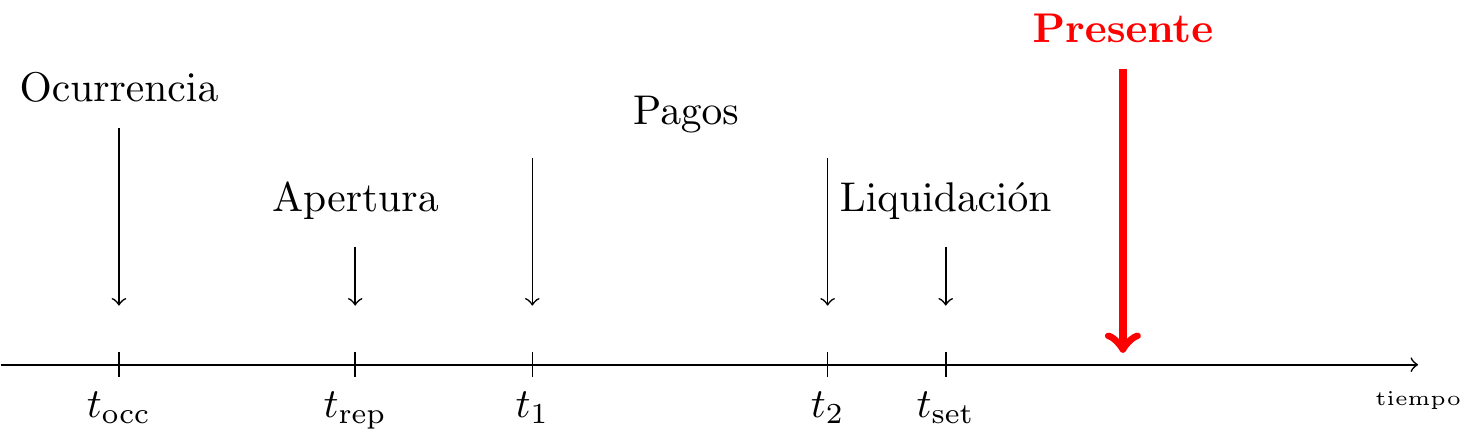
Figure 11.2: Vida de un siniestro cerrado
Un siniestro RBNS ha sido comunicado pero no está completamente liquidado (Reported But Not Settled) en el momento actual o en el momento de la evaluación, es decir, el momento en que las provisiones deben ser calculadas y reservadas por el asegurador. La ocurrencia, la notificación y posiblemente algunos pagos tienen lugar antes del momento presente, pero el cierre del siniestro ocurre en el futuro, más allá del momento presente.
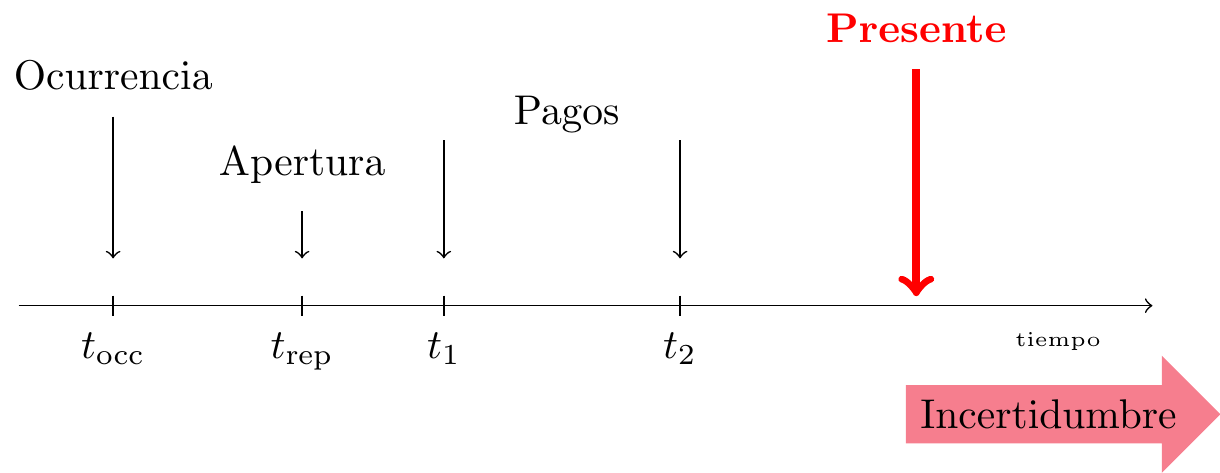
Figure 11.3: Vida de un siniestro RBNS
Un siniestro IBNR ha ocurrido en el pasado pero aún no ha sido comunicado (Incurred But Not yet Reported). El evento asegurado ocurrió, pero la compañía de seguros aún no está al tanto del siniestro asociado. Esta reclamación se comunicará en el futuro y su desarrollo completo (desde la comunicación hasta la liquidación) tendrá lugar en el futuro.
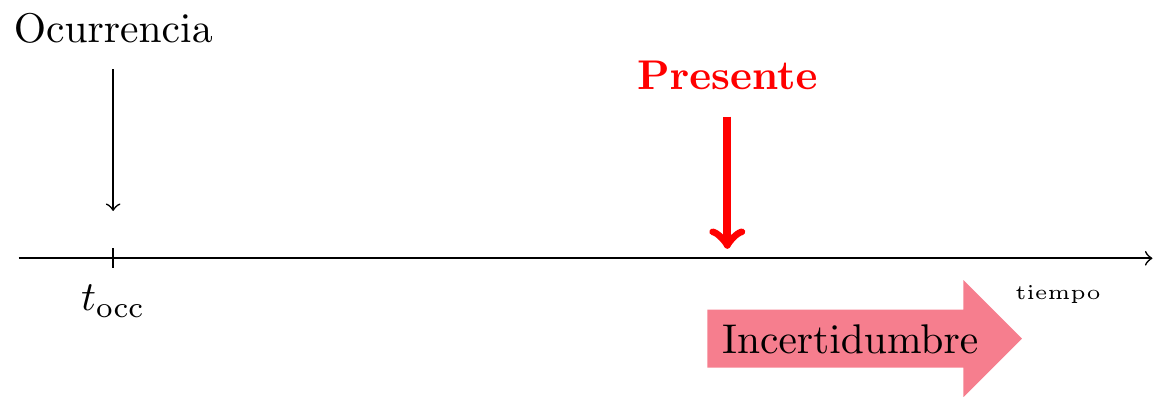
Figure 11.4: Vida de un siniestro IBNR
Las compañías de seguros provisionarán el capital para cumplir con sus responsabilidades futuras con respecto a los siniestros tanto RBNS como IBNR. El desarrollo futuro de tales siniestros es incierto y se utilizarán técnicas de modelización predictiva para calcular las reservas adecuadas, a partir de los datos históricos de desarrollo observados en siniestros similares.
11.1.2 ¿Por qué reservar?
El ciclo de producción invertido del mercado de los seguros y la dinámica de los siniestros que se muestra en la sección 11.1.1 motivan la necesidad de reservar y el diseño de herramientas de modelización predictiva para estimar las reservas. En los seguros, los ingresos por primas preceden a los costes. Un asegurador cobrará una prima a un cliente, antes de saber realmente cómo de costosa será la póliza o el contrato de seguro. En la industria manufacturera normalmente no es así y el fabricante sabe - antes de vender un producto - cuál fue el coste de producción de este producto. En un momento de evaluación específico \(\tau\) el asegurador predecirá sus responsabilidades pendientes con respecto a los contratos vendidos en el pasado. Esta es la reserva de siniestros o reserva para pérdidas; es el capital necesario para liquidar los siniestros abiertos de exposiciones pasadas. Es un elemento muy importante en el balance del asegurador, más concretamente en el pasivo de este balance.
11.2 Datos de provisiones
11.2.1 De Micro a Macro
Ahora analizamos los datos disponibles para estimar la reserva pendiente de una cartera de contratos P&C. Las compañías de seguros suelen registrar los datos sobre el desarrollo de un siniestro individual como se muestra en la línea de tiempo a la izquierda de la figura 11.5. Nos referimos a los datos registrados a este nivel como datos granulares o de micro-nivel. Típicamente, un actuario agrega la información registrada sobre la evolución individual de los siniestros para todas las reclamaciones de una cartera. Esta agregación da lugar a datos estructurados en un formato triangular como se muestra en la parte derecha de la figura 11.5. Estos datos se denominan datos agregados o a nivel macro porque cada celda del triángulo muestra la información obtenida al agregar el desarrollo de múltiples reclamaciones.
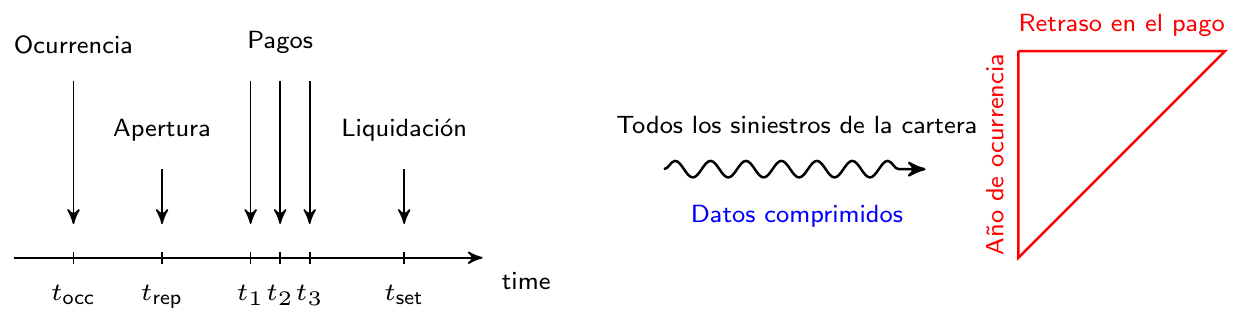
Figure 11.5: De datos granulares a triángulo de desarrollo
La visualización triangular utilizada en la provisión por pérdidas se llama triángulo run-off o de desarrollo. En el eje vertical el triángulo enumera los años de accidente o de ocurrencia durante los cuales se sigue una cartera. Los pagos provisionados para un siniestro específico están conectados con el año durante el cual ocurrió el evento asegurado. En el eje horizontal se indica el retraso en el pago desde la ocurrencia del evento asegurado.
11.2.2 Triángulos de desarrollo
Un primer ejemplo de un triángulo de desarrollo con pagos incrementales se muestra en la Figura 11.6 (tomada de Wüthrich and Merz (2008), Tabla 2.2, también utilizada en Wüthrich and Merz (2015), Tabla 1.4). Los años de los accidentes (o años de ocurrencia) se muestran en el eje vertical y van desde 2004 hasta 2013. Se refieren al año durante el cual ocurrió el evento asegurado. El eje horizontal indica el retraso en el pago en años desde la ocurrencia del evento asegurado. 0 retraso se utiliza para los pagos realizados en el año de ocurrencia del accidente o evento asegurado. Un año de retraso se utiliza para los pagos realizados en el año posterior a la ocurrencia del accidente.
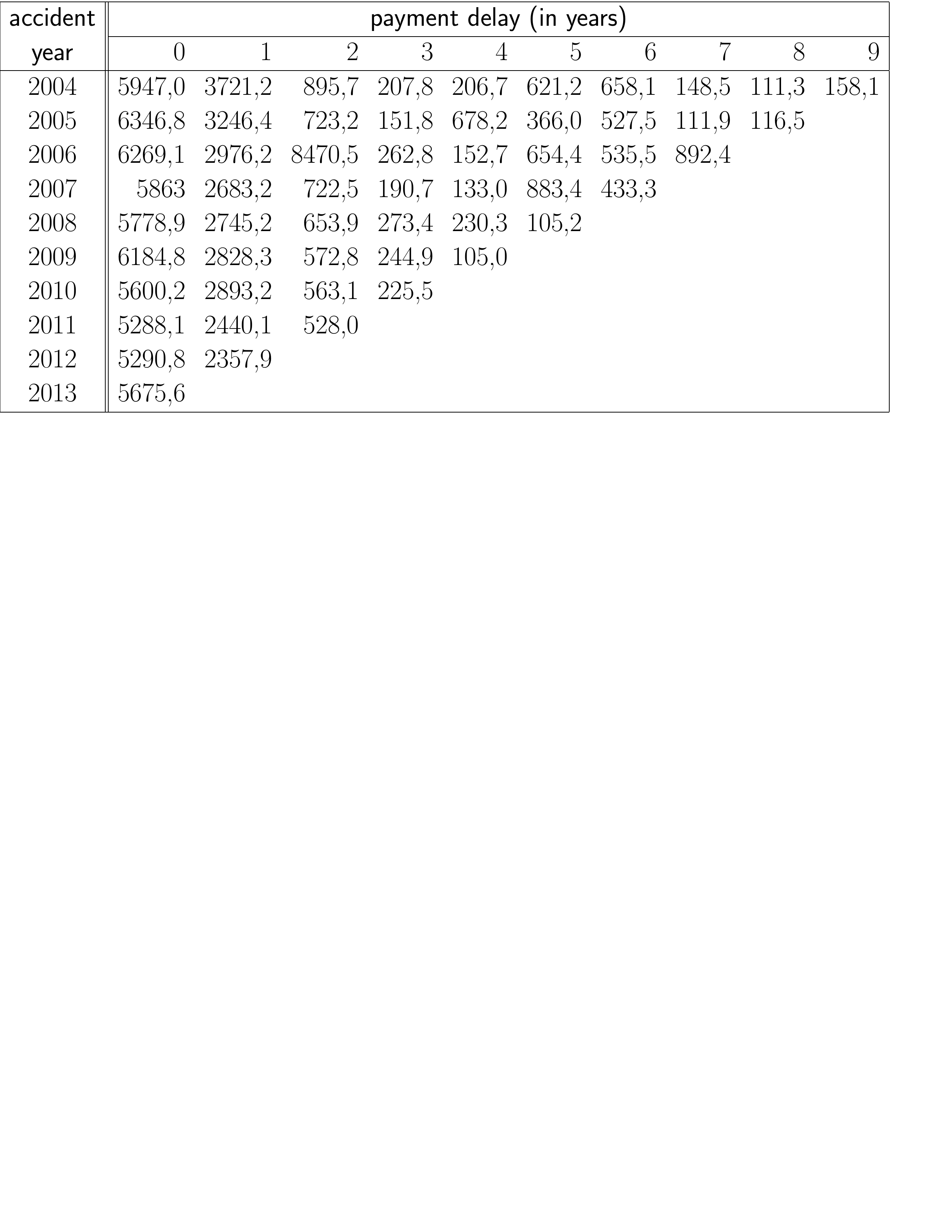
Figure 11.6: Triángulo de Desarrollo con datos de pagos incrementales. Fuente: Wüthrich and Merz (2008), Tabla 2.2.
Por ejemplo, la celda \((2004, 0)\) del triángulo anterior muestra el número \(5947\), la cantidad total pagada en el año 2004 por todas los siniestros ocurridos en el año 2004. Por lo tanto, es la cantidad total pagada con 0 años de retraso en todas las reclamaciones que ocurrieron en el año 2004. De manera similar, el número de la celda \((2012,1)\) muestra el total de \(2357,9\) pagados en el año 2013 por todos los siniestros que ocurrieron en el año 2012.
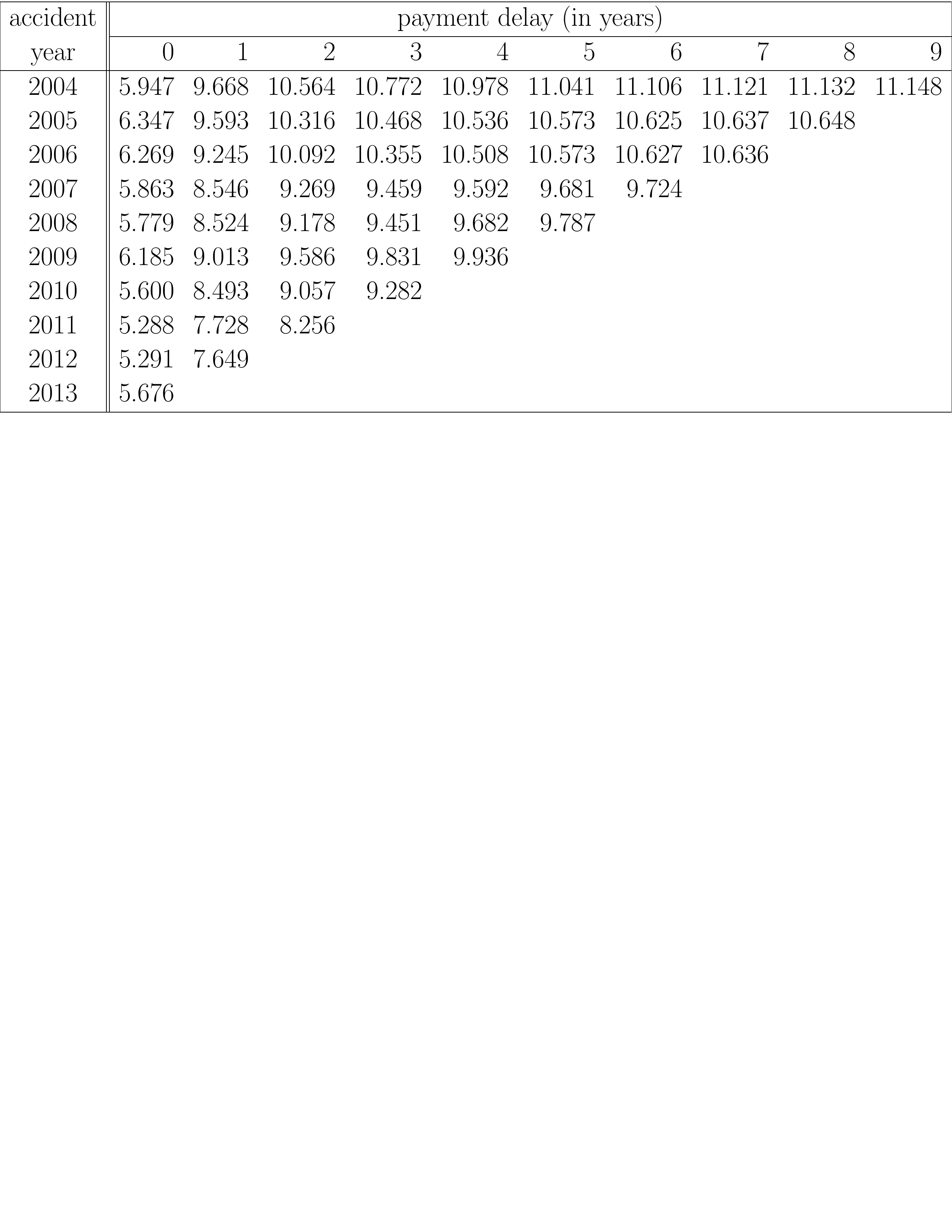
Figure 11.7: Triángulo de desarrollo con datos de pago acumulados. Fuente: Wüthrich and Merz (2008), Tabla 2.2.
Mientras que el triángulo de la Figura 11.6 muestra los datos de pago incremental, la Figura 11.7 muestra la misma información en formato acumulado. Ahora, la celda \((2004,1)\) muestra la cantidad total pagada hasta la demora de pago 1 para todos los siniestros que ocurrieron en el año 2004. Por lo tanto, es la suma de la cantidad pagada en 2004 y la cantidad pagada en 2005 por los accidentes que ocurrieron en 2004.
Se pueden utilizar diferentes datos en triángulos de desarrollo como los que se muestran en la Figura 11.6 y en la Figura 11.7. Dependiendo del tipo de datos utilizados, el triángulo se utilizará para estimar diferentes cantidades.
Por ejemplo, en el formato incremental una celda puede mostrar:
- los pagos de los siniestros, como explicado antes
- el número de reclamaciones que se produjeron en un año específico y que se notificaron con cierto retraso, cuando el objetivo es estimar el número de siniestros IBNR
- la variación en las cantidades incurridas, donde las cantidades incurridas de los siniestros son la suma de los siniestros pagados acumulados y las estimaciones individuales. La estimación individual es la estimación del tramitador de los siniestros sobre la cantidad pendiente de pago de un siniestro.
En el formato acumulado una celda puede mostrar:
- la cantidad pagada acumulada, según lo explicado antes
- el número total de siniestros de un año de ocurrencia, notificados hasta un determinado retraso
- las cantidades incurridas de los siniestros.
Es posible que se disponga de otras fuentes de información, por ejemplo, covariables (como el tipo de siniestros), información externa (como inflación, cambios regulatorios). La mayoría de los métodos de provisión de siniestros diseñados para los triángulos de desarrollo se basan más bien en una sola fuente de información, aunque algunas contribuciones recientes se centran en el uso de datos más detallados para la provisión de pérdidas.
11.2.3 Notación de provisiones
Triángulos de desarrollo
Para formalizar lo mostrado en las figuras 11.6 y 11.7, permitimos que \(i\) se refiera al año de ocurrencia o accidente, el año en que ocurrió el evento asegurado. En nuestra anotación el primer año de accidente considerado en la cartera se denota con 1 y el último año de accidente, el más reciente, se denota con \(I\). De la misma forma, \(j\) se refiere al año de retraso de pago o desarrollo, donde un retraso igual a 0 corresponde al año de accidente. La figura 11.8 muestra un triángulo en el que se considera el mismo número de años en la dirección vertical y en la horizontal, por lo que \(j\) va desde 0 hasta \(J = I-1\).
Figure 11.8: Notación matemática para un triángulo de desarrollo. Fuente: Wüthrich and Merz (2008)
La variable aleatoria \(X_{ij}\) denota las reclamaciones incrementales pagadas en el período de desarrollo \(j\) de los siniestros del año de accidente \(i\). Por lo tanto, \(X_{ij}\) es la cantidad total pagada en el año de desarrollo \(j\) por todos los siniestros que ocurrieron en el año de ocurrencia \(i\). Estas cuantías se pagan realmente en el año contable o natural \(i+j\). Desde un punto de vista acumulado, \(C_{ij}\) es la cantidad acumulada pagada hasta (e incluyendo) el año de desarrollo \(j\) por los accidentes ocurridos en el año \(i\). Al final, se paga una cantidad total de \(C_{iJ}\) en el último año de desarrollo \(J\) por los siniestros ocurridos en el año de accidente \(i\). En este capítulo el tiempo se expresa en años, aunque también se pueden utilizar otras unidades de tiempo, por ejemplo, semestres o trimestres.
Provisión por pérdidas
En el momento de la evaluación \(\tau\), se han observado los datos del triángulo superior, mientras que el triángulo inferior tiene que predecirse. Aquí, el momento de la evaluación es el final del año del accidente \(I\) lo que implica que una celda \((i,j)\) con \(i+j \leq I\) se observa, y una celda \((i,j)\) con \(i+j > I\) pertenece al futuro y tiene que ser predicha. Así, para un triángulo de desarrollo acumulado, el objetivo de un método de provisión de pérdidas es predecir \(C_{i,I-1}\), la cantidad última por los siniestros para el año de ocurrencia \(i\), correspondiente al período final de desarrollo \(I-1\) en la Figura 11.7. Asumimos que - más allá de este período - no habrá más pagos, aunque este supuesto puede relajarse.
Dado que \(C_{i,I-1}\) es acumulado, incluye tanto una parte observada como una parte que debe predecirse. Por lo tanto, la provisión por pagos pendientes para el año de accidente \(i\) es
\[\begin{eqnarray*} \mathcal{R}^{(0)}_{i} = \sum_{\ell=I-i+1}^{I-1} X_{i\ell} = C_{i,I}-C_{i,I-i}. \end{eqnarray*}\]
Expresamos la reserva como una suma de datos incrementales, \(X_{i\ell}\), o como la diferencia entre datos acumulados. En este último caso, la cantidad pendiente es la cantidad acumulada final \(C_{i,I}\) menos la cantidad acumulada observada más reciente \(C_{i,I-i}\). Siguiendo a Wüthrich and Merz (2015), la anotación \(\mathcal{R}^{(0)}_{i}\) se refiere a la reserva para el año de ocurrencia \(i\) donde \(i=1,\ldots,I\). El superíndice \((0)\) se refiere a la evaluación de la reserva en el momento actual, digamos \(\tau = 0\). Entendemos que \(\tau = 0\) al final del año de ocurrencia \(I\), el año calendario más reciente para el que se observan y registran los datos.
11.2.4 Código R para resumir datos de provisión de pérdidas
Usamos el paquete ChainLadder (Gesmann et al. 2019) para importar triángulos de desarrollo en R y para explorar las tendencias presentes en estos triángulos. La viñeta del paquete documenta muy bien sus funciones para trabajar con datos triangulares. Primero, exploramos dos formas de importar un triángulo.
Datos con formato extenso
El conjunto de datos triangle_W_M_long.txt almacena el triángulo de desarrollo acumulado de Wüthrich and Merz (2008) (Tabla 2.2) en formato largo. Es decir, cada celda del triángulo es una fila de este conjunto de datos, y se almacenan tres características: la cuantía del pago (acumulado, en este ejemplo), el año de ocurrencia (\(i\)) y el retraso del pago (\(j\)). Importamos el archivo .txt y almacenamos el conjunto de datos resultante como my_triangle_long:
Código R para importar datos de texto
Usamos la función as.triangle del paquete ChainLadder para transformar el conjunto de datos en formato triangular. El objeto resultante my_triangle ahora es de tipo triangle.
Código R para la transformación en formato triangular
Mostramos el triángulo y reconocemos los números (en miles) de la figura 11.7. Las celdas en el triángulo inferior se indican como valores ausentes (not available), NA.
Código R para mostrar datos triangulares
Datos en formato triangular
Alternativamente, el triángulo puede ser almacenado en un archivo .csv con los años de ocurrencia en las filas y los años de desarrollo en las celdas de la columna. Importamos este archivo .csv y transformamos my_triangle_csv resultante en una matriz.
Código R para importar datos triangulares
Inspeccionamos el triángulo:
Código R para mostrar datos triangulares
De acumulado a incremental y viceversa
Las funciones de R cum2incr() y incr2cum() nos permiten pasar de datos acumulados a incrementales, y viceversa, de una manera fácil.
Código R para pasar de visualización de datos acumulados a incrementales
Reconocemos el triángulo incremental de la figura 11.6.
Visualización de triángulos
Para explorar la evolución de los pagos acumulados por año de ocurrencia, la figura 11.9 muestra my_triangle usando la función plot disponible para los objetos de tipo triangle en el paquete ChainLadder. Cada línea de este gráfico muestra un año de ocurrencia (de 2004 a 2013, etiquetado como 1 a 10). Los períodos de desarrollo se etiquetan de 1 a 10 (en lugar de 0 a 9, como se usó anteriormente).
plot(my_triangle)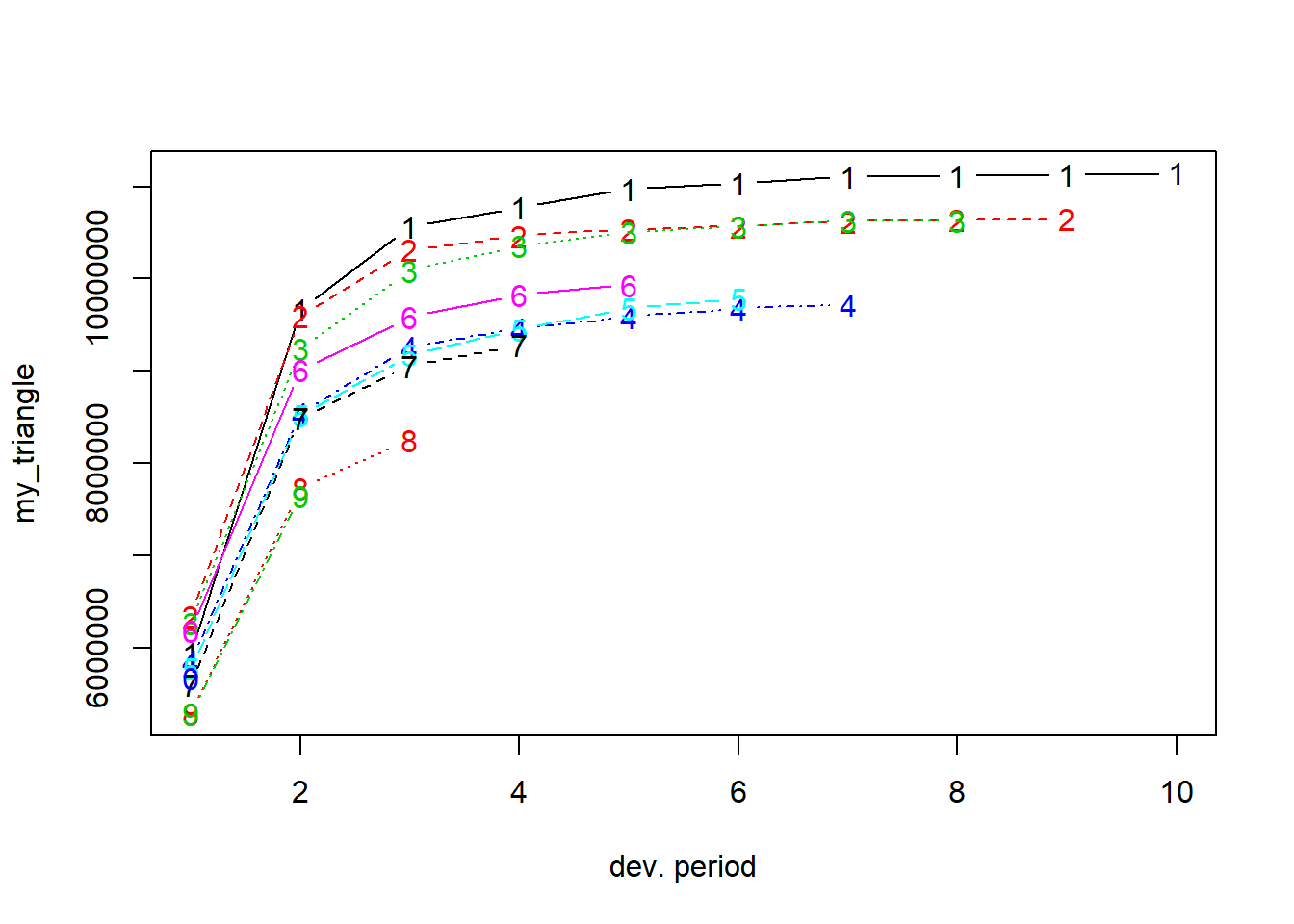
Figure 11.9: Desarrollo del siniestro por año de ocurrencia
Alternativamente, el argumento lattice crea un gráfico por año de ocurrencia.
plot(my_triangle, lattice = TRUE)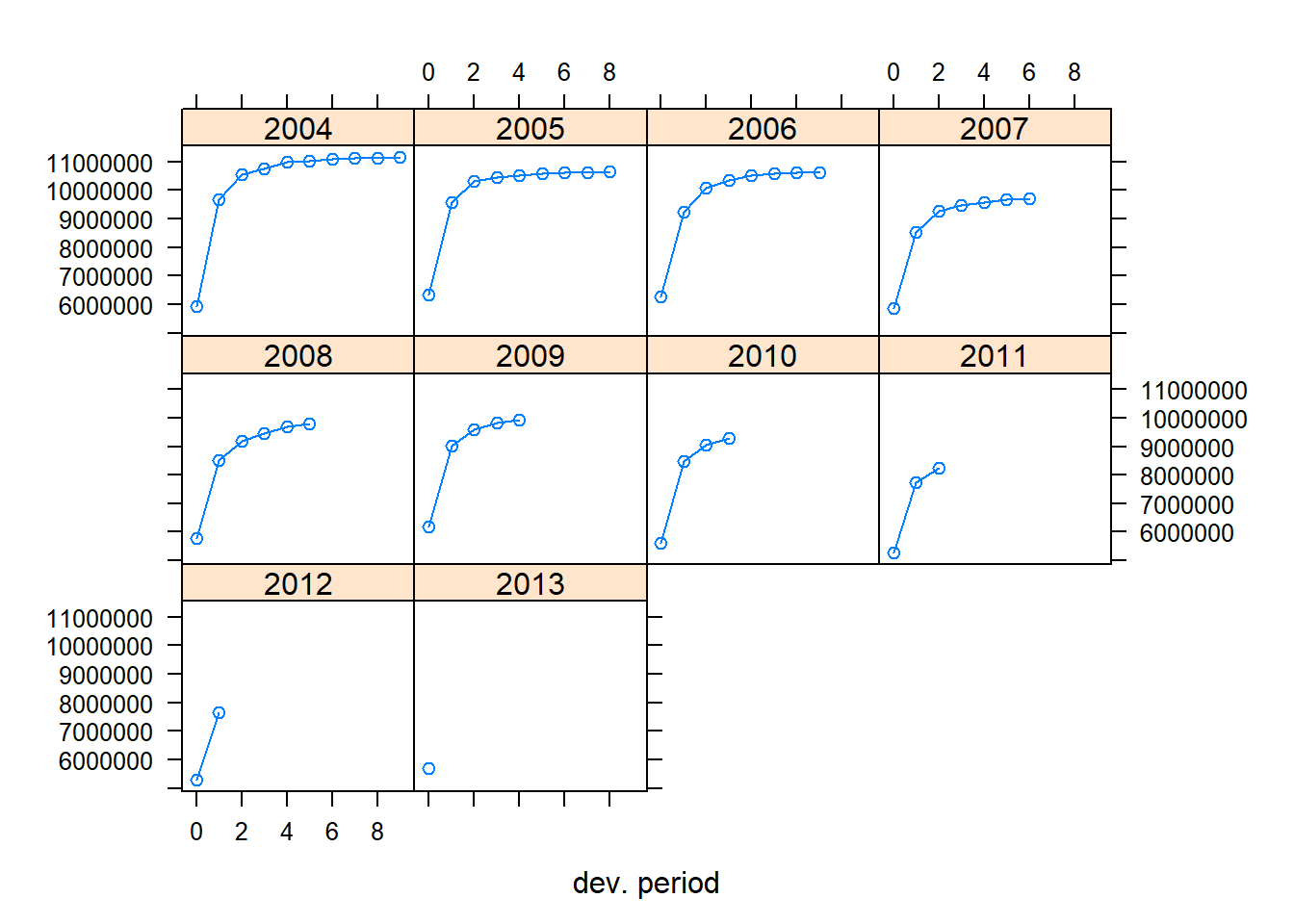
En lugar de graficar el triángulo acumulado guardado en my_triangle, podemos graficar el triángulo de desarollo incremental.
plot(my_triangle_incr)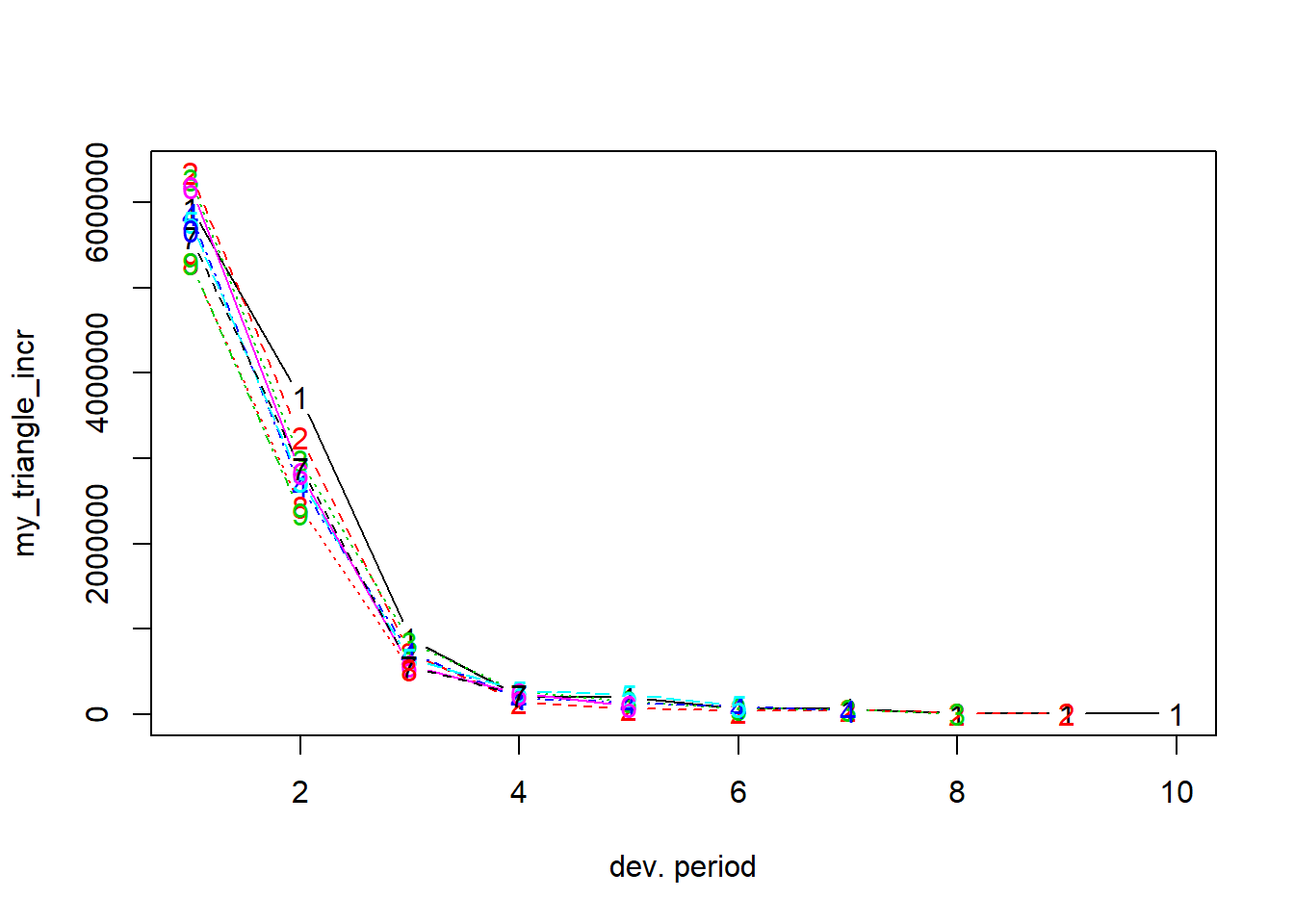
plot(my_triangle_incr, lattice = TRUE)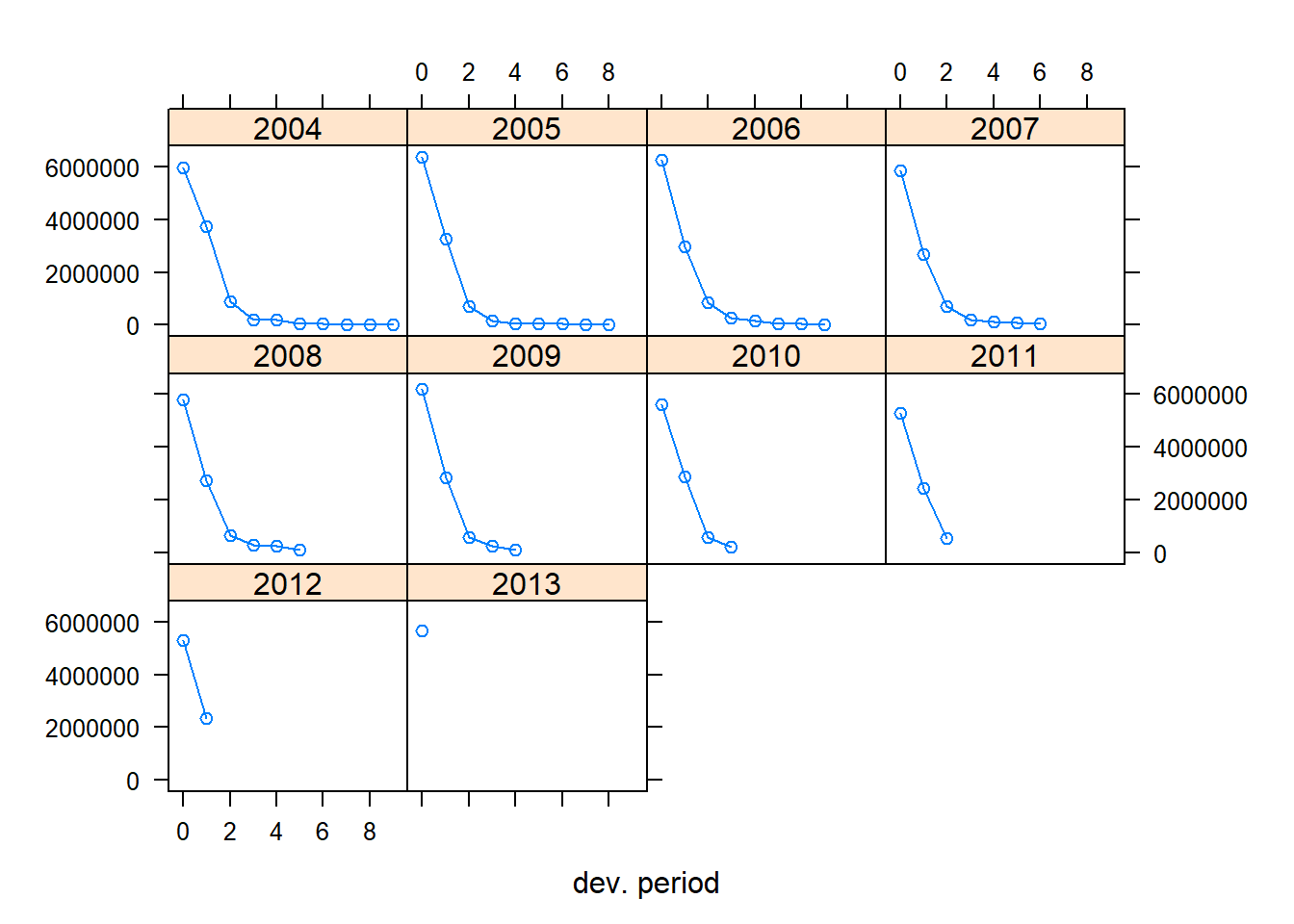
11.3 Chain-Ladder
El método más utilizado para estimar las reservas por pagos pendientes es el llamado método chain-ladder. Los orígenes de este método no están claros pero se afianzó firmemente en aplicaciones prácticas a principios de los 70, G. C. Taylor (1986). Como se mostrará, el nombre se refiere al encadenamiento (chain) de una secuencia de factores (desarrollo año a año) en una escalera (ladder) de factores; las pérdidas inmaduras suben hacia la madurez cuando se multiplican por esta concatenación de ratios, de ahí la descripción de método chain-ladder. Empezaremos explorando el método chain-ladder en su versión determinista o algorítmica, por lo tanto sin hacer ninguna suposición estocástica. Luego describiremos el modelo chain-ladder de distribución libre de Mack.
11.3.1 Chain-Ladder Determinista
El método chain-ladder determinista se centra en el triángulo de desarrollo en forma acumulada. Recordemos que una celda \((i,j)\) en este triángulo muestra la cantidad acumulada pagada hasta el período de desarrollo \(j\) por siniestros que ocurrieron en el año \(i\). El método chain-ladder asume que los factores de desarrollo \(f_j\) (también llamados factores edad-a-edad, ratios de enlace o factores chain-ladder) existen de tal manera que
\[ C_{i,j+1} = f_j \times C_{i,j}. \]
Por tanto, el factor de desarrollo indica cómo la cantidad acumulada en el año de desarrollo \(j\) crece hasta la cantidad acumulada en el año \(j+1\). Destacamos la cantidad acumulada en el período 0 en azul y la cantidad acumulada en el período 1 en rojo en la Figura 11.10 tomada de Wüthrich and Merz (2008) (Tabla 2.2, también utilizada en Wüthrich and Merz (2015), Tabla 1.4).
Figure 11.10: Triángulo de desarrollo con datos de pagos acumulados que muestra la cantidad acumulada en el período 0 en azul y la cantidad acumulada en el período 1 en rojo. Fuente: Wüthrich and Merz (2008), Tabla 2.2.
El método chain-ladder presenta una forma intuitiva para estimar o calcular estos factores de desarrollo. Dado que el primer factor de desarrollo \(f_0\) describe el desarrollo de la cantidad acumulada de los siniestros desde el período de desarrollo 0 hasta el período de desarrollo 1, se puede estimar como la proporción de las cantidades acumuladas en rojo y las cantidades acumuladas en azul, resaltadas en la Figura 11.10. En notación matemática obtenemos entonces la siguiente estimación \(\hat{f}_0^{CL}\) para el primer factor de desarrollo \(f_0\), dadas las observaciones \(\mathcal{D}_I\):
\[ \hat{f}^{CL}_{\color{magenta}{0}} = \frac{\sum_{i=1}^{10-\color{magenta}{0}-1} \color{red}{C_{i,\color{magenta}{0}+1}}}{\sum_{i=1}^{10-\color{magenta}{0}-1} \color{blue}{C_{i\color{magenta}{0}}}}= 1,4925. \]
Cabe señalar que el índice \(i\), utilizado en las sumas del numerador y el denominador, va desde el primer período de ocurrencia (1) hasta el último período de ocurrencia (9) para el que se observan ambos períodos de desarrollo 0 y 1. Como tal, este factor de desarrollo mide cómo los datos en azul crecen hasta los datos en rojo, promediados a través de todos los períodos de ocurrencia para los cuales se observan ambos períodos. El método chain-ladder utiliza entonces este estimador del factor de desarrollo para predecir la cantidad acumulada \(C_{10,1}\) (es decir, la cantidad acumulada pagada hasta el año de desarrollo 1 inclusive por los accidentes ocurridos en el año 10). Esta predicción se obtiene multiplicando la cantidad acumulada de siniestros más reciente observada para el período de ocurrencia 10 (es decir, \(C_{10,0}\) con el período de desarrollo 0) por el factor de desarrollo estimado \(\hat{f}^{CL}_0\): \[ \hat{C}_{10, 1} = C_{10,0} \cdot \hat{f}^{CL}_0 = 5.676\cdot 1,4925=8.471. \] Siguiendo este razonamiento, se puede estimar el próximo factor de desarrollo \(f_1\). Dado que \(f_1\) captura el desarrollo del período 1 al período 2, puede ser estimado como la proporción de los números en rojo y los números en azul como se resalta en la Figura 11.11.
Figure 11.11: Triángulo de desarrollo con datos de pago acumulado que muestra la cantidad acumulada en el período 1 en azul y la cantidad acumulada en el período 2 en rojo. Fuente: Wüthrich and Merz (2008), Tabla 2.2.
La notación matemática de la estimación de \(\hat{f}_1^{CL}\) para el siguiente factor de desarrollo \(f_1\), dadas las observaciones \(\mathcal{D}_I\), es igual:
\[ \hat{f}^{CL}_{\color{magenta}{1}} = \frac{\sum_{i=1}^{10-\color{magenta}{1}-1} \color{red}{C_{i,\color{magenta}{1}+1}}}{\sum_{i=1}^{10-\color{magenta}{1}-1} \color{blue}{C_{i\color{magenta}{1}}}}=1,0778. \]
Por consiguiente, este factor mide cómo la cantidad acumulada pagada en el período de desarrollo 1 crece hasta el período 2, promediada en todos los períodos de ocurrencia en los que se observan ambos períodos. El índice \(i\) va ahora del período 1 al 8, ya que estos son los períodos de ocurrencia para los que se observan ambos períodos de desarrollo 1 y 2. Esta estimación del segundo factor de desarrollo se utiliza entonces para predecir las casillas que faltan y no se observan en el período de desarrollo 2:
\[ \begin{array}{rl} \hat{C}_{10,2} &= C_{10,0} \cdot \hat{f}^{CL}_0 \cdot \hat{f}_1^{CL} = \hat{C}_{10,1} \cdot \hat{f}_1^{CL} = 8471 \cdot 1,0778 = 9130 \\ \hat{C}_{9,2} &= C_{9,1} \cdot \hat{f}^{CL}_1 = 7649 \cdot 1,0778 = 8244. \end{array} \] Note que para \(\hat{C}_{10,2}\) realmente se usa la estimación \(\hat{C}_{10,1}\) y se multiplica por el factor de desarrollo estimado \(\hat{f}_1^{CL}\).
Continuamos de manera análoga y obtenemos las siguientes predicciones, mostradas en cursiva en la Figura 11.12:
![Triángulo de desarollo con datos de pago acumulados que incluyen predicciones en cursiva. Fuente: [@WuthrichMerz2008], Tabla 2.2.](LossDataAnalytics_files/figure-html/tikz-cum-triangle-cl3-1.png)
Figure 11.12: Triángulo de desarollo con datos de pago acumulados que incluyen predicciones en cursiva. Fuente: (Wüthrich and Merz 2008), Tabla 2.2.
Eventualmente se necesita estimar los valores de la columna final. El último factor de desarrollo \(f_8\) mide el crecimiento desde el período de desarrollo 8 al período de desarrollo 9 en el triángulo. Como sólo en la primera fila del triángulo se han observado ambas celdas, este último factor se estima como la relación entre el valor en rojo y el valor en azul en la Figura 11.13.
![Triángulo de desarollo con datos de pago acumulado en los que se destaca la cantidad acumulada en el período 8 en azul y la cantidad acumulada en el período 9 en rojo. Fuente: [@WuthrichMerz2008], Tabla 2.2.](LossDataAnalytics_files/figure-html/tikz-cum-triangle-cl3b-1.png)
Figure 11.13: Triángulo de desarollo con datos de pago acumulado en los que se destaca la cantidad acumulada en el período 8 en azul y la cantidad acumulada en el período 9 en rojo. Fuente: (Wüthrich and Merz 2008), Tabla 2.2.
Dadas las observaciones \(\mathcal{D}_I\), este factor estimado es igual a: \[ \hat{f}^{CL}_{\color{magenta}{8}} = \frac{\sum_{i=1}^{10-\color{magenta}{8}-1} \color{red}{C_{i,\color{magenta}{8}+1}}}{\sum_{i=1}^{10-\color{magenta}{8}-1} \color{blue}{C_{i\color{magenta}{8}}}}=1,001. \] Frecuentemente este último factor de desarrollo es cercano a 1 y por lo tanto los flujos de caja pagados en el período final de desarrollo son menores. Utilizando esta estimación del factor de desarrollo, podemos ahora estimar los costes de los siniestros acumulados que faltan en la columna multiplicando los valores del año de desarrollo 8 con este factor.
La notación matemática general para las predicciones chain-ladder para el triángulo inferior (\(i+j>I\)) es la siguiente:
\[ \begin{array}{rl} \hat{C}_{ij}^{CL} &= C_{i,I-i} \cdot \prod_{l=I-i}^{j-1} \hat{f}_l^{CL} \\ \hat{f}_j^{CL} &= \frac{\sum_{i=1}^{I-j-1} C_{i,j+1}}{\sum_{i=1}^{I-j-1} C_{ij}}, \end{array} \] donde \(C_{i,I-i}\) está en la última diagonal observada. Es evidente que una suposición importante del método chain-ladder es que los desarrollos proporcionales de siniestros de un período de desarrollo a otro son similares para todos los años de ocurrencia.
Esto da como resultado la siguiente Figura 11.14:
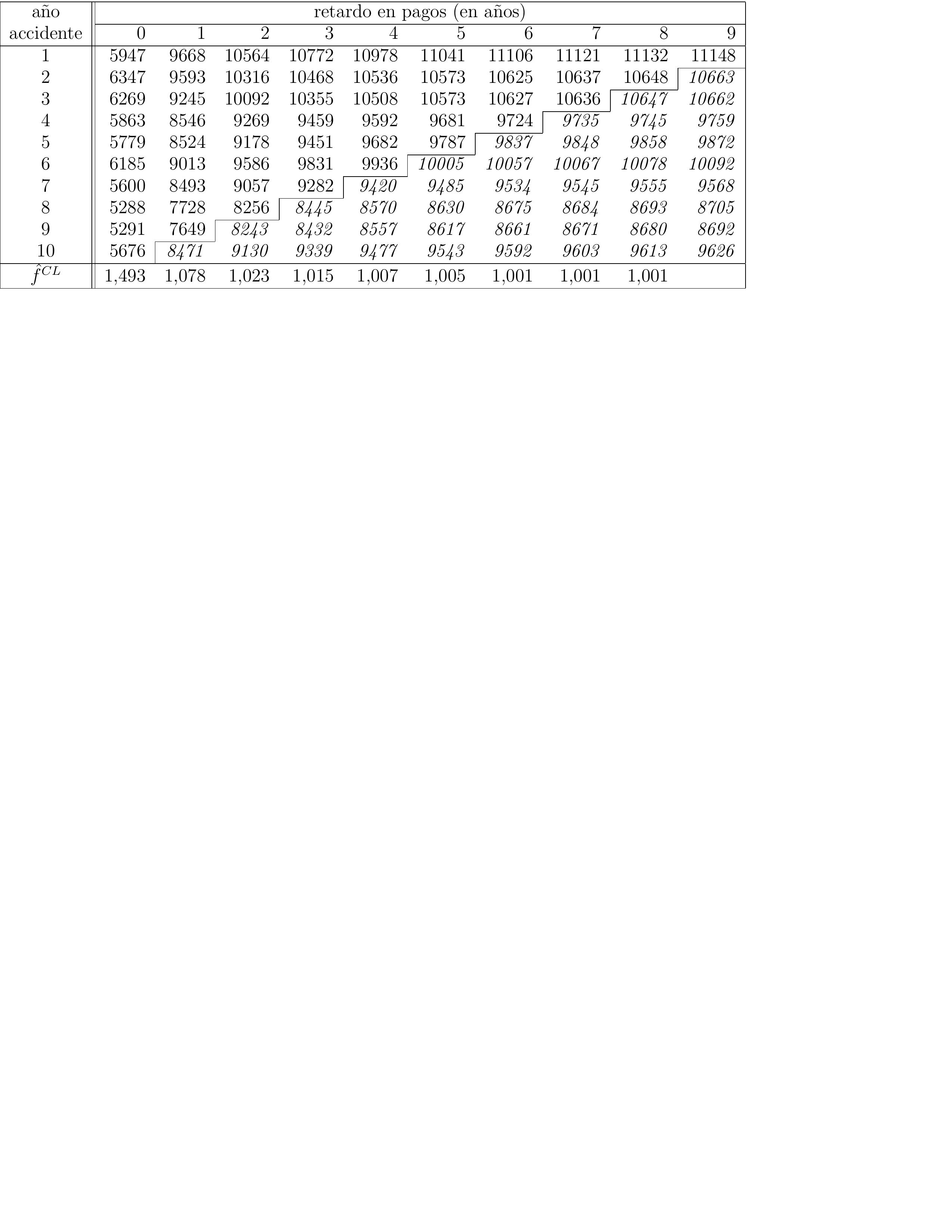
Figure 11.14: Triángulo de desarrollo con datos de pagos acumulados en el que se incluyen las predicciones en cursiva. Fuente: Wüthrich and Merz (2008), Tabla 2.2.
Las cifras de la última columna muestran las estimaciones de las cantidades finales de los siniestros. La estimación de la cantidad pendiente \(\hat{\mathcal{R}}_i^{CL}\) para un particular año de ocurrencia \(i=I-J+1,\ldots, I\) viene dada por la diferencia entre la cantidad última y la cantidad acumulada observada en la diagonal más reciente: \[ \hat{\mathcal{R}}_i^{CL} =\hat{C}_{iJ}^{CL}-C_{i,I-i}. \] Esta es la estimación chain-ladder de la provisión necesaria para cumplir con las responsabilidades futuras con respecto a los siniestros que ocurrieron en este período de ocurrencia en particular. Estas reservas por período de ocurrencia y para el total sumado de todos los períodos de ocurrencia se resumen en la Figura 11.15.
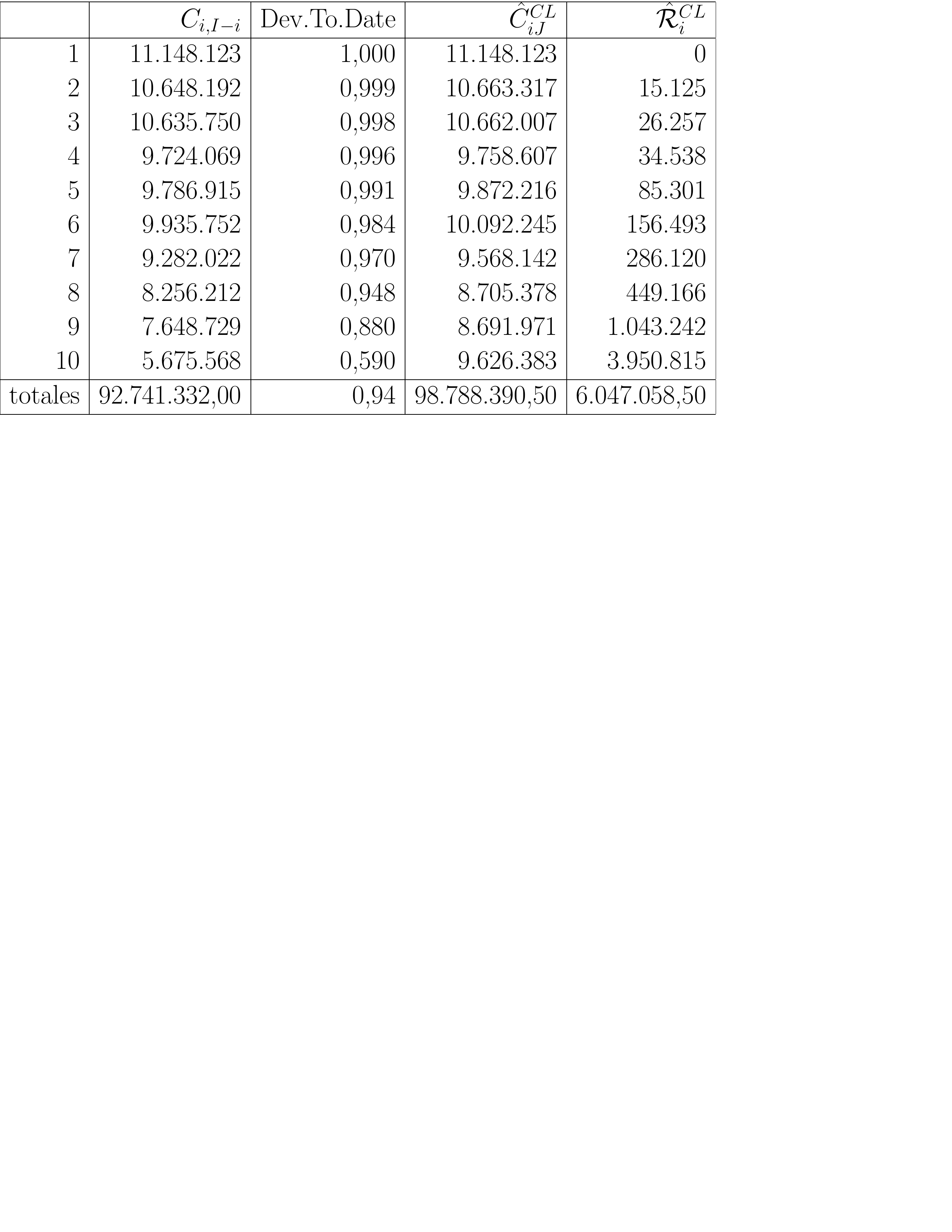
Figure 11.15: Reservas por período de ocurrencia y para el total
11.3.2 Modelo Chain-ladder de distribución libre de Mack
En esta etapa, el método tradicional chain-ladder proporciona un estimador puntual \(\hat{C}^{CL}_{iJ}\) para el pronóstico de \(C_{iJ}\), usando la información \(\mathcal{D}_I\). Dado que el método de chain-ladder es un algoritmo puramente determinista e intuitivamente natural para completar un triángulo de desarrollo, no se puede determinar cómo de fiable es el estimador puntual ni modelizar la variación de los pagos futuros. Para responder a tales preguntas se necesita un modelo estocástico subyacente que reproduzca las estimaciones de las provisiones chain-ladder.
En esta sección nos centraremos en el modelo chain-ladder de distribución libre como modelo estocástico subyacente, introducido en Mack (1993). Este método nos permite estimar los errores estándar de las predicciones chain-ladder. En la siguiente sección 11.4, se utilizan modelos lineales generalizados para desarrollar un enfoque totalmente estocástico para predecir la reserva pendiente.
En el enfoque de Mack se mantienen las siguientes condiciones (sin asumir una distribución):
Los siniestros acumulados \((C_{ij})_{j=0,\ldots,J}\) son independientes a lo largo de diferentes periodos de ocurrencia \(i\).
Existen constantes fijas \(f_0, \ldots, f_{J-1}\) y \(\sigma^2_0,\ldots, \sigma^2_{J-1}\) tal que para todo \(i=1,\ldots, I\) y \(j=0,\ldots,J-1\):
\[ \begin{array}{rl} E[C_{i,j+1}|C_{i0},\ldots,C_{ij}] &= f_j \cdot C_{ij} \\ \text{Var}(C_{i,j+1}|C_{ij}) &= \sigma^2_j \cdot C_{ij}. \end{array} \]
Esto significa que los siniestros acumulados \((C_{ij})_{j=0,\ldots,J}\) son procesos de Markov (en los períodos de desarrollo \(j\)) y por lo tanto el futuro sólo depende del presente.
Con estos supuestos, el valor esperado de la cantidad de pagos final \(C_{i,J}\), dados los datos disponibles en el triángulo superior, es la cantidad acumulada en la diagonal más reciente (\(C_{i, I-1}\)) multiplicada por los factores de desarrollo apropiados \(f_j\). En notación matemática obtenemos para los factores de desarrollo conocidos \(f_j\) y las observaciones \(\mathcal{D}_I\):
\[ E[C_{iJ}|\mathcal{D}_I] = C_{i,I-i} \prod_{j=I-i}^{J-1} f_j. \] Esto es exactamente lo que hace el método de chain-ladder determinista, como se explica en la sección 11.3.1. En la práctica, los factores de desarrollo no se conocen y necesitan ser estimados a partir de los datos que están disponibles en el triángulo superior. En el enfoque de Mack obtenemos exactamente la misma expresión para estimar los factores de desarrollo \(f_j\) en el tiempo \(I\) que en el algoritmo determinista de chain-ladder: \[ \hat{f}_j^{CL} =\frac{\sum_{j=1}^{I-j-1} C_{i,j+1}}{\sum_{i=1}^{I-j-1} C_{ij}}. \] Las predicciones para las celdas del triángulo inferior (es decir, para las celdas \(C_{i,j}\) donde \(i+j>I\)) se obtienen entonces reemplazando los factores desconocidos \(f_j\) por sus correspondientes estimaciones \(\hat{f}_j^{CL}\): \[ \hat{C}^{CL}_{ij} = C_{i,I-i}\prod_{l=I-i}^{j-1} \hat{f}_l^{CL}. \]
Para cuantificar el error de predicción de las predicciones de chain-ladder, Mack también introdujo parámetros de varianza \(\sigma^2_j\). Para comprender mejor la estimación de estos parámetros de varianza, se introducen los llamados factores de desarrollo individual \(f_{i,j}\) (que son específicos del período de ocurrencia \(i\)):
\[ f_{i,j} = \frac{C_{i,j+1}}{C_{ij}}. \] Estos factores de desarrollo individuales también describen cómo la cantidad acumulada crece desde el período \(j\) hasta el período \(j+1\), pero consideran la proporción de sólo dos celdas (en lugar de tomar la proporción de dos sumas sobre todos los períodos de ocurrencia disponibles).
Obsérvese que los factores de desarrollo pueden escribirse como un promedio ponderado de los factores de desarrollo individual: \[ \hat{f}_j^{CL} = \sum_{i=1}^{I-j-1} \frac{C_{ij}}{\sum_{i=1}^{I-j-1} C_{ij}} f_{i,j}, \] donde los pesos son iguales a los siniestros acumulados \(C_{ij}\).
Estimemos ahora los parámetros de varianza \(\sigma^2\) escribiendo el supuesto de la varianza de Mack de manera equivalente.
Primero, la varianza de la relación de \(C_{i,j+1}\) y \(c_{i,j}\) condicionada a \(C_{i,0},\ldots, C_{i,j}\) es proporcional a la inversa de \(C_{i,j}\):
\[ \text{Var}[C_{i,j+1}/C_{ij}|C_{i0},\ldots,C_{ij}] ~ \propto ~ \frac{1}{C_{ij}}. \]
Esto tiene la estructura de mínimos cuadrados ponderados donde los pesos son la inversa de la variabilidad de una respuesta. Por lo tanto, una variable de respuesta más volátil o imprecisa tendrá menos peso. Los \(C_{i,j}\) juegan el papel de los pesos. Usando el parámetro de varianza desconocida \(\sigma^2_j\) esta suposición de varianza puede escribirse como:
\[ \text{Var}[C_{i,j+1}|C_{i0},\ldots,C_{ij}] = \sigma^2_j \cdot C_{ij}, \] La conexión con los mínimos cuadrados ponderados nos conduce directamente a una estimación insesgada del parámetro de varianza desconocida \(\sigma^2_j\) en forma de suma ponderada de residuos al cuadrado: \[ \hat{\sigma}^2_j = \frac{1}{I-j-2}\sum_{i=1}^{I-j-1} C_{ij}\left(\frac{C_{i,j+1}}{C_{ij}}-\hat{f}_j^{CL}\right)^2. \] Los pesos son de nuevo iguales a \(C_{i,j}\) y los residuos son las diferencias entre las ratios \(C_{i,j+1}/C_{i,j}\) y los factores de desarrollo individual.
Ahora tenemos todos los ingredientes necesarios para calibrar el modelo chain-ladder de distribución libre con los datos. El siguiente paso es analizar la incertidumbre de la predicción y el error de predicción. Aquí usamos el predictor de chain-ladder donde reemplazamos los factores de desarrollo desconocidos con sus estimadores:
\[ \hat{C}_{iJ}^{CL} = C_{i,I-i} \prod_{l=I-i}^{J-1} \hat{f}_l^{CL} \]
Utilizamos esta expresión como estimador de la esperanza condicional de la cantidad de pagos final (dado el triángulo superior observado) o como predictor de la cantidad de pagos final como variable aleatoria (dado el triángulo superior observado).
En estadística, la medida más simple para analizar la incertidumbre que viene con una estimación puntual o predicción es el Error Cuadrado Medio de Predicción (MSEP, según sus siglas en inglés). Aquí consideramos un MSEP condicional, condicionado a los datos observados en el triángulo superior:
\[ MSEP_{C_{iJ}|\mathcal{D}_I}\left(\hat{C}_{iJ}^{CL}\right) = E\left[\left(C_{iJ}-\hat{C}_{iJ}^{CL}\right)^2|\mathcal{D}_I\right]. \]
El MSEP condicional mide:
- la distancia entre el (verdadero) coste final \(C_{iJ}\) y su predictor chain-ladder \(\hat{C}_{iJ}^{CL}\) en el tiempo \(I\), y
- la incertidumbre total de la predicción sobre la totalidad del desarrollo del coste nominal final \(C_{iJ}\). No se considera ni el valor del tiempo del dinero, ni margen de riesgo ni ninguna dinámica en los desarrollos.
El MSEP de la estimación de la cantidad final de siniestros acumulada es igual al MSEP que mide la distancia cuadrada entre la provisión verdadera y la estimada:
\[ \begin{array}{rl} MSEP_{\hat{\mathcal{R}}^{I}_{i}|\mathcal{D}_I}(\hat{\mathcal{R}}^{I}_i) &= E[(\hat{\mathcal{R}}^I_i-\mathcal{R}^I_i)^2|\mathcal{D}_I] \\ &= E[(\hat{C}^{CL}_{iJ}-C_{iJ})^2|\mathcal{D}_I] = MSEP(\hat{C}_{iJ}). \end{array} \] La razón de esta equivalencia es el hecho de que la provisión es el coste último de los siniestros menos el coste de los siniestros observado más reciente. Este último se observa y usa en \(\mathcal{R}^I_i\) y \(\hat{\mathcal{R}}^I_i\).
Es interesante descomponer este MSEP en un componente que capture la varianza del proceso y un componente que capture la varianza de la estimación de los parámetros:
\[ \begin{array}{rl} MSEP_{C_{iJ|\mathcal{D}_I}}\left(\hat{C}_{iJ}^{CL}\right) &= E\left[ \left( C_{iJ} - \hat{C}_{iJ} \right)^2 | \mathcal{D}_I\right] \\ &= \text{Var}(C_{iJ}|\mathcal{D}_I) + \left( E[C_{iJ}|\mathcal{D}_I]-\hat{C}_{iJ}^{CL} \right)^2 \\ &= \color{magenta}{\text{varianza del proceso}} + \color{magenta}{\text{ varianza de la estimación de los parámetros}}, \end{array} \]
para un \(\mathcal{D}_I\) medible estimador/predictor de \(\hat{C}_{iJ}\). El componente de la varianza del proceso captura la volatilidad o incertidumbre en la variable aleatoria \(C_{i,J}\) y la varianza de la estimación del parámetro mide el error que surge al sustituir los factores de desarrollo desconocidos \(f_j\) por sus valores estimados. Este resultado se deriva inmediatamente de la siguiente igualdad sobre la varianza de una variable aleatoria desplazada \(X\) donde el desplazamiento \(a\) es determinístico:
\[ E(X-a)^2 = \text{Var}(X)+\left[EX-a\right]^2. \]
Aplicado a la expresión del MSEP se trata a \(\hat{C}_{i,J}\) como fijo porque se trabaja condicionalmente en los datos del triángulo superior y \(\hat{C}_{i,J}\) sólo usa la información de este triángulo superior.
Mack (1993) derivó la importante fórmula para el MSEP condicional en el modelo chain-ladder de distribución libre para un único período de ocurrencia \(i\):
\[ \widehat{MSEP_{C_{iJ}|\mathcal{D}_I}} = \left(\hat{C}_{iJ}^{CL}\right)^2 \sum_{j=I-i}^{J-1} \left[ \frac{\hat{\sigma}_j^2}{(\hat{f}_j^{CL})^2} \left(\frac{1}{\hat{C}^{CL}_{ij}}+\frac{1}{\sum_{n=1}^{I-j-1}C_{nj}}\right)\right]. \]
Para la derivación de esta fórmula popular, nos remitimos a su artículo. Nótese que es una estimación del MSEP ya que los parámetros desconocidos \(f_j\) y \(\sigma_j\) necesitan ser estimados y el error de estimación no puede calcularse explícitamente.
Mack también derivó una fórmula para el MSEP para la provisión total, a través de todos los períodos de ocurrencia:
\[ \begin{array}{ll} \widehat{MSEP_{\sum_{i=1}^I \hat{C}^{CL}_{iJ}}}\left( \sum_{i=1}^I \hat{C}^{CL}_{iJ} \right) \\ \ \ \ \ \ \sum_{i=1}^I \widehat{MSEP_{C_{iJ}|\mathcal{D}_I}}\left( \hat{C}^{CL}_{iJ} \right) \color{blue}{+2 \sum_{1\leq i< k \leq I} \hat{C}_{iJ}^{CL} \hat{C}_{kJ}^{CL} \sum_{j=I-i}^{J-1} \frac{ \hat{\sigma}_j^2/\left( \hat{f}_j^{\text{CL}} \right)^2 }{ \sum_{n=1}^{I-j-1} C_{nj} }}. \end{array} \] El resultado es la suma de los MSEP por período de ocurrencia más un término de covarianza. Este término de covarianza se suma porque los MSEPs para diferentes períodos de ocurrencia \(i\) utilizan los mismos estimadores \(\hat{f}_j^{CL}\) de los parámetros \(f_j\) para diferentes años de accidentes \(i\).
11.3.3 Código R para las predicciones Chain-Ladder
Usamos el objeto my_triangle de tipo triangle que se creó en la sección 11.2.4. El modelo chain-ladder de distribución libre de Mack (1993) está implementado en el paquete ChainLadder (Gesmann et al. 2019) (como una forma especial de mínimos cuadrados ponderados) y puede ser aplicado en los datos my_triangle para predecir las cuantías de los siniestros pendientes y para estimar el error estándar de estas predicciones.
Código R para las predicciones del modelo Mack
Los factores de desarrollo se obtienen de la siguiente manera:
round(CL$f,digits = 4) [1] 1.4925 1.0778 1.0229 1.0148 1.0070 1.0051 1.0011 1.0010 1.0014 1.0000Código R para el triángulo completo modelo de Mack
La MSEP para la reserva total a través de todos los períodos de ocurrencia se obtiene como:
CL$Total.Mack.S.E^2 9
214348469061 Se deben validar los supuestos de Mack comprobando que no hay tendencias en los gráficos de los residuos. Los últimos cuatro gráficos que obtenemos con el siguiente comando muestran respectivamente los residuos estandarizados frente a los valores ajustados, el período de origen, el período de calendario y el período de desarrollo.
plot(CL)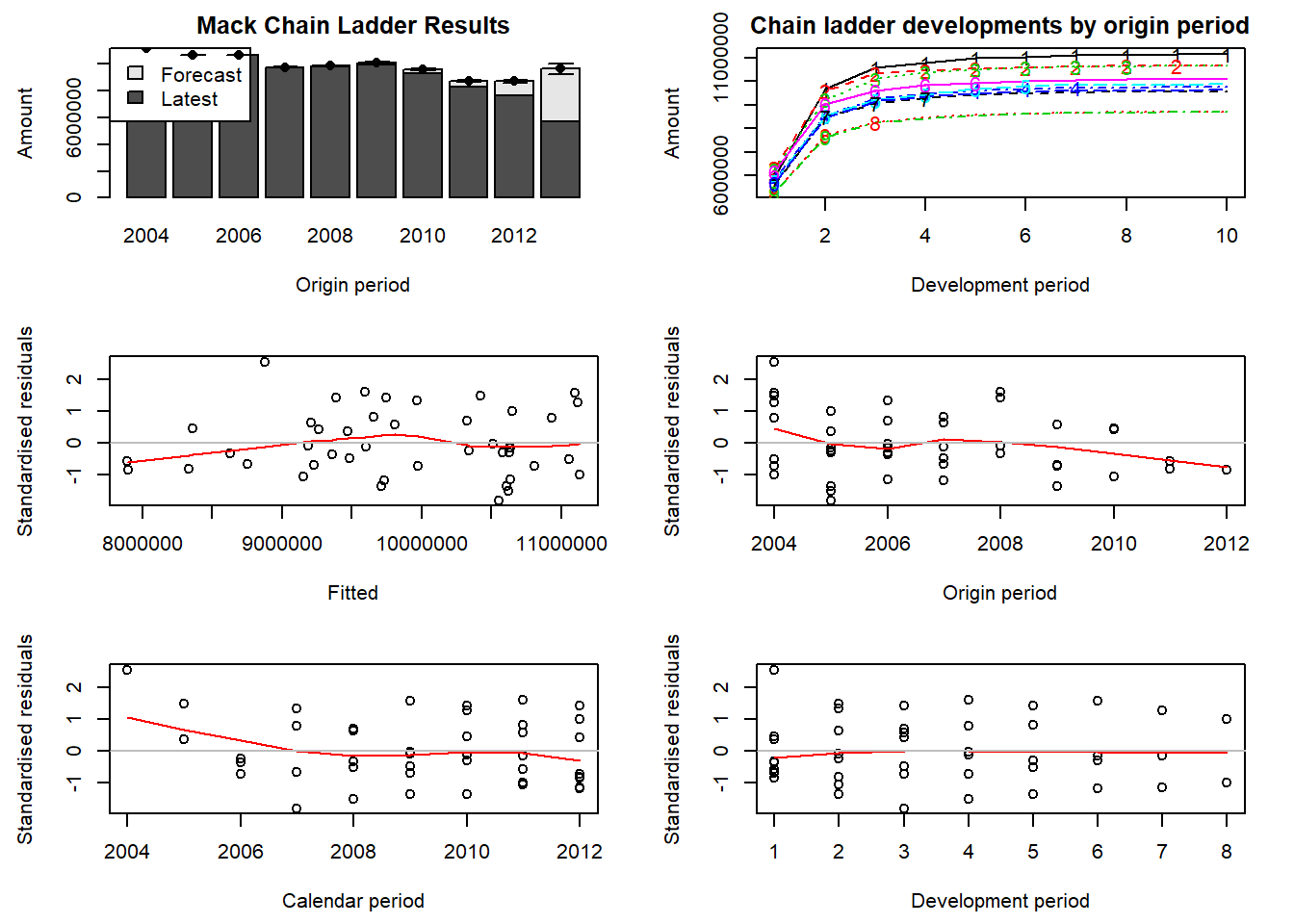
El gráfico superior izquierdo es un gráfico de barras de la última posición de los siniestros más el IBNR y el error estándar de Mack por período de ocurrencia. El gráfico superior derecho muestra los patrones de desarrollo predichos para todos los períodos de ocurrencia (comenzando con 1 para el período de ocurrencia más antiguo).
Al establecer el argumento lattice=TRUE se obtiene un gráfico del desarrollo, incluyendo la predicción y los errores estándar estimados por período de ocurrencia:
plot(CL, lattice=TRUE)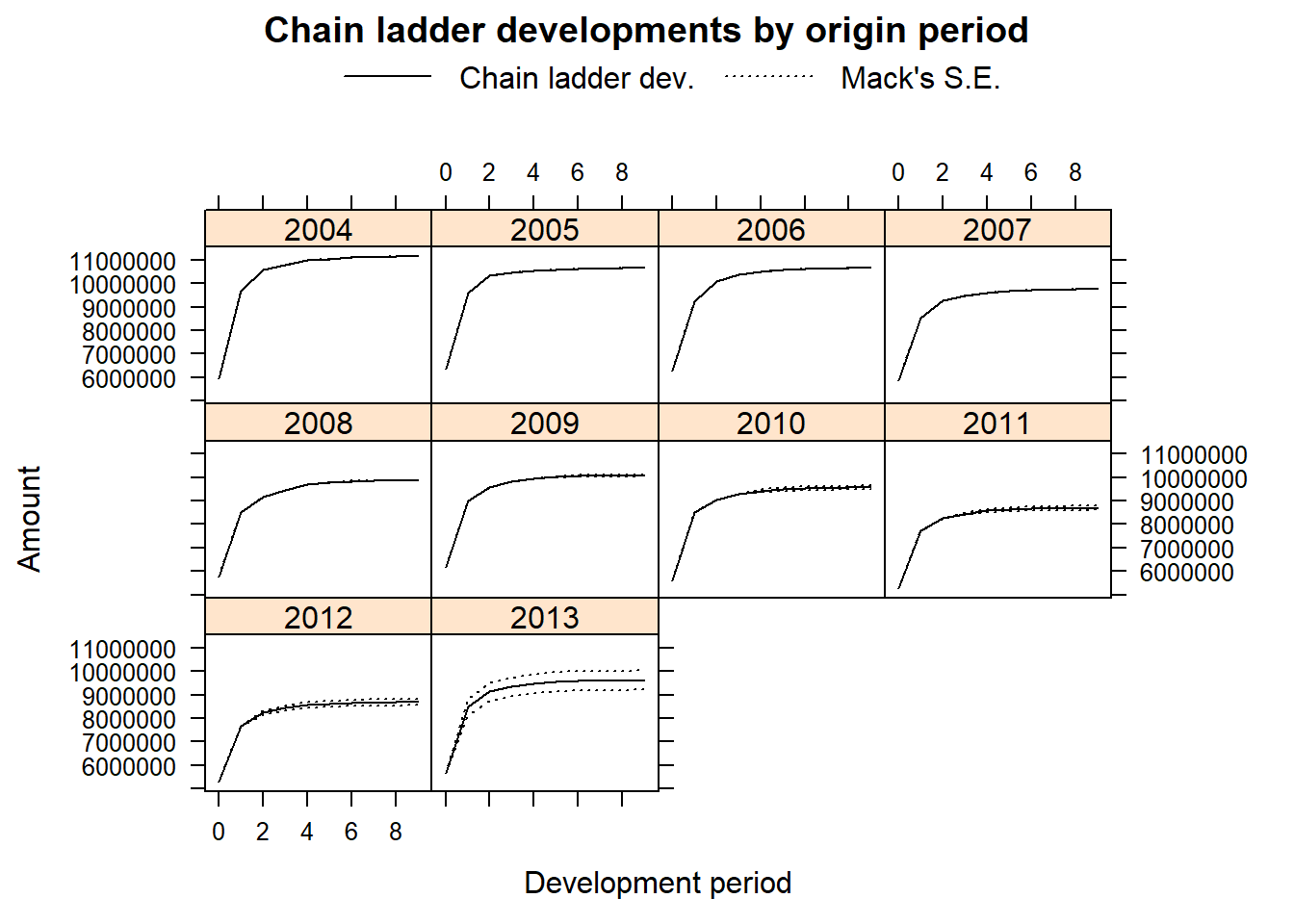
11.4 GLMs y Bootstrap para provisiones
** Esta sección se está escribiendo y aún no está completa ni editada. Os mostramos una idea de lo que será la versión final.**
Esta sección cubre los modelos de regresión para analizar los triángulos de desarrollo. Cuando se analizan los datos de un triángulo de desarrollo con un modelo de regresión, se dispone de los instrumentos estándar para la construcción, estimación y predicción del modelo. Usando estas herramientas somos capaces de ir más allá de la estimación puntual y el error estándar como se deriva en la Sección 11.3. Más específicamente, construimos un modelo lineal generalizado (GLM) para los pagos incrementales \(X_{ij}\) en la Figura 11.6. Mientras que el método de chain-ladder funciona con datos acumulados, los GLM asumen que las variables de respuesta son independientes y por lo tanto trabajan con triángulos de desarrollo incrementales.
11.4.1 Especificación del modelo
Suponemos que \(X_{ij}\) denota el pago incremental en la celda \((i,j)\) del triángulo de desarrollo. Asumimos que los \(X_{ij}\) son independientes con una densidad \(f(x_{ij};\theta_{ij},\phi)\) de la familia exponencial de distribuciones. Identificamos
- \(\mu_{ij}=E[X_{ij}]\) el valor esperado de la celda \(X_{ij}\)
- \(\phi\) el parámetro de dispersion y \(\text{Var}[X_{ij}]=\phi \cdot V(\mu_{ij})\), donde \(V(.)\) es la función varianza.
- \(\eta_{ij}\) el predictor lineal tal \(\eta_{ij}=g(\mu_{ij})\) con \(g\) la función enlace.
Las distribuciones de la familia exponencial y sus funciones de enlace por defecto se enumeran en http://stat.ethz.ch/R-manual/R-patched/library/stats/html/family.html. Ahora analizamos tres GLM específicos ampliamente utilizados para la reserva de pérdidas.
Primero, el modelo de regresión de Poisson fue introducido en la sección 8.2. En este modelo, asumimos que \(X_{ij}\) tiene una distribución de Poisson con el parámetro
\[ \mu_{ij} = \pi_i \cdot \gamma_j, \]
una estructura cruzada que capta un efecto multiplicador del año de ocurrencia \(i\) y el período de desarrollo \(j\). La estructura del modelo propuesto no es identificable sin una restricción adicional en los parámetros, por ejemplo \(\sum_{j=0}^J \gamma_j=1\). Esta restricción da una interpretación explícita a \(\pi_i\) (con \(i=1,\ldots,I\)) como la medida de exposición o volumen para el año de ocurrencia \(i\) y \(\gamma_j\) como la fracción del volumen total pagado con retraso \(j\). Sin embargo, cuando se calibran los GLM en R, las restricciones alternativas como \(\pi_1=1\) o \(\gamma_1=1\), o una reparametrización donde \(\mu_{ij} = \exp{(\mu+\alpha_i+\beta_j)}\) son más fáciles de implementar. Continuamos con esta última especificación, incluyendo \(\alpha_1 = \beta_0 = 0\), denominadas restricciones de esquina. Este GLM trata el año de ocurrencia y el retraso de pago como variables categóricas y ajusta un parámetro por nivel, junto a una constante \(\mu\). Las restricciones de esquina establecen que el efecto del primer nivel de una variable factorial sea igual a cero. La distribución de Poisson es particularmente útil para un triángulo de desarrollo con número de siniestros comunicados, a menudo utilizado en la estimación del número de siniestros IBNR (véase la sección 11.2).
En segundo lugar, una interesante modificación del modelo básico de regresión de Poisson es el modelo de regresión de Poisson sobredisperso donde \(Z_{ij}\) tiene una distribución de Poisson con parámetro \(\mu_{ij}/\phi\) y
\[ \begin{array}{rl} X_{ij} &\sim \phi \cdot Z_{ij} \\ \mu_{ij} &= \exp{(\mu + \alpha_i + \beta_j)}. \end{array} \]
De este modo, \(X_{ij}\) tiene la misma especificación para la media que en el modelo básico de regresión de Poisson, pero ahora \[ \text{Var}[X_{ij}] = \phi^2 \cdot \text{Var}[Z_{ij}] = \phi \cdot \exp{(\mu + \alpha_i + \beta_j)}. \]
Esta construcción permite la subdispersión (cuando \(\phi <1\)) y la sobredispersión (con \(\phi>1\)). Dado que \(X_{ij}\) ya no sigue una distribución conocida, este enfoque se denomina cuasiprobabilidad. Es particularmente útil para modelar un triángulo de desarrollo con pagos incrementales, ya que éstos normalmente muestran sobredispersión.
En tercer lugar, el modelo de regresión gamma es adecuado para modelizar un triángulo de desarrollo con pagos de siniestros. Recordemos la sección 3.2.1 (véase también el capítulo del apéndice 18) con parámetros \(\alpha\) y \(\theta\). A partir de aquí, reparametrizamos y definimos un nuevo parámetro \(\mu = \alpha \cdot \theta\) mientras se mantiene el parámetro de escala \(\theta\). Además, se asume que \(X_{ij}\) tiene una distribución gamma y se permite que \(\mu\) varíe con \(ij\) de tal manera que
\[ \mu_{ij} = \exp{(\mu + \alpha_i + \beta_j)}. \]
11.4.2 Estimación y predicción del modelo
Se estiman los parámetros de regresión \(\mu\), \(\alpha_i\) y \(\beta_j\) en los GLM propuestos. En R está disponible la función glm para estimar estos parámetros a través de la estimación por máxima verosimilitud (mle) o cuasi-verosimilitud (en el caso de Poisson sobredisperso). Teniendo disponibles las estimaciones de los parámetros \(\hat{\mu}\), \(\hat{\alpha}_i\) y \(\hat{\beta}_j\), se obtiene una estimación puntual para cada celda del triángulo superior
\[
\hat{X}_{ij} =\hat{E[X_{ij}]} = \exp{(\hat{\mu}+\hat{\alpha}_i+\hat{\beta}_j)},\ \text{con}\ i+j\leq I.
\]
Similarly, a cell in the lower triangle will be predicted as
De manera similar, se puede predecir una celda en el triángulo inferior como
\[
\hat{X}_{ij} = \hat{E[X_{ij}]} = \exp{(\hat{\mu}+\hat{\alpha}_i+\hat{\beta}_j)},\ \text{con}\ i+j> I.
\]
Luego se suman las estimaciones específicas de cada celda para obtener estimaciones puntuales de las reservas pendientes (por año de ocurrencia \(i\) o la provisión total). Combinando las observaciones del triángulo superior con sus estimaciones puntuales, podemos obtener residuos adecuadamente definidos y usarlos para la inspección de los residuos.
11.4.3 Bootstrap
11.5 Recursos adicionales y contribuciones
Colaboradores
- Katrien Antonio, KU Leuven y University of Amsterdam, Jan Beirlant, KU Leuven, y Tim Veerdonck, University of Antwerp, son los autores principals de la version inicial de este capítulo. Email: katrien.antonio@kuleuven.be para comentarios y posibles mejoras del capítulo.
- Traducción al español: Miguel Santolino (Universitat de Barcelona)
Lecturas adicionales y referencias
Como se muestra en la Figura 11.1, cronogramas y visualizaciones similares se discuten (entre otros) en Wüthrich and Merz (2008), Antonio and Plat (2014) y Wüthrich and Merz (2015).
Con el tiempo los actuarios comenzaron a pensar en posibles modelos subyacentes. Aquí mencionamos algunas contribuciones importantes:
- E. Kremer (1982): ANOVA de dos factores
- Erhard Kremer (1984), Mack (1991): modelo Poisson
- Mack (1993): modelo chain-ladder de distribución-libre
- A. E. Renshaw (1989); A. Renshaw and Verrall (1998): modelo Poisson sobredisperso
- Gisler (2006); Gisler and Wüthrich (2008); Bühlmann et al. (2009): modelo chain-ladder bayesiano.
Los diversos modelos estocásticos propuestos en la literatura actuarial se basan en diferentes supuestos y tienen diferentes propiedades, pero tienen en común que proporcionan exactamente las estimaciones de la provisión chain-ladder. Para más información también nos referimos a Mack and Venter (2000) y a la interesante discusión que se publicó en el ASTIN Bulletin: Journal of the International Actuarial Association en 2006 (Gary G. Venter 2006).
Para leer más sobre las familias exponenciales y los modelos lineales generalizados, ver, por ejemplo, P. McCullagh and Nelder (1989) y Wüthrich and Merz (2008). Nos referimos a (E. Kremer 1982), (A. Renshaw and Verrall 1998) y (England and Verrall 2002), y a los resúmenes en (G. Taylor 2000), (Wüthrich and Merz 2008) y (Wüthrich and Merz 2015) para más detalles sobre los GLM analizamos. XXX presenta supuestos distributivos y especificaciones alternativas del predictor lineal.