Chapter 13 Datos y Sistemas

Vista Previa del Capítulo. Este capítulo cubre las áreas de aprendizaje sobre datos y sistemas de información según el Plan Educativo de la IAA (International Actuarial Association, según sus siglas en inglés) publicado en septiembre de 2015. Este capítulo está organizado en tres grandes partes: datos, análisis de datos y técnicas de análisis de datos. La primera parte introduce conceptos básicos de datos, tales como tipos, estructuras, almacenamiento y fuentes de datos. La segunda parte discute el proceso y varios aspectos del análisis de datos. La tercera parte presenta algunas técnicas usadas comúnmente para el análisis de datos.

13.1 Datos

13.1.1 Tipos y Fuentes de Datos

En términos de cómo son recolectados los datos, éstos pueden ser divididos en dos tipos (Hox and Boeije 2005): datos primarios y datos secundarios. Los datos primarios son datos originales que son recolectados para un problema específico de investigación. Los datos secundarios son originalmente recolectados para un propósito diferente y reutilizados para otro problema de investigación. Una gran ventaja de usar datos primarios es que la construcción teórica, el diseño de la investigación y la estrategia de la recolección de datos puede ser ajustada a la pregunta de investigación subyacente para asegurar que los datos recolectados en verdad ayudan a resolver el problema. Una desventaja de usar datos primarios es que la recolección de datos puede ser costosa y consume tiempo. Usar datos secundarios tiene la ventaja de menor costo y más rápido acceso a la información relevante. Sin embargo, el uso de datos secundarios puede no ser óptimo para la pregunta de investigación que se está considerando.

En términos de los grados de organización de los datos, estos también pueden ser divididos en dos tipos (Inmon and Linstedt 2014; O’Leary 2013; Hashem et al. 2015; Abdullah and Ahmad 2013; Pries and Dunnigan 2015): datos estructurados y datos no estructurados. Los datos estructurados tienen un formato predecible y de ocurrencia regular. Por el contrario, los datos no estructurados son impredecibles y no tienen una estructura que sea reconocible por un computador. Los datos estructurados consisten de registros, atributos, claves e índices y, por lo general, son administrados por un sistema de administración de bases de datos (DBMS, según sus siglas en inglés) como IBM DB2, Oracle, MySQL y Microsoft SQL Server. Como resultado, la mayoría de las unidades de datos estructurados se pueden localizar rápida y fácilmente. Los datos no estructurados tienen muchas formas y variaciones diferentes. Una forma común de datos no estructurados es el texto. Acceder a datos no estructurados es complicado. Para encontrar una unidad de datos determinada en un texto extenso, por ejemplo, usualmente se realiza una búsqueda secuencial.

En términos de cómo son medidos los datos, se pueden clasificar en cualitativos o cuantitativos. Los datos cualitativos son datos sobre cualidades, que en realidad no se pueden medir. Como resultado, los datos cualitativos son de naturaleza extremadamente variada e incluyen entrevistas, documentos y artefactos. (Miles, Hberman, and Sdana 2014). Los datos cuantitativos son datos sobre cantidades, los cuales se pueden medir numéricamente con números. En términos del nivel de medición, los datos cuantitativos pueden además ser clasificados como nominales, ordinales, intervalares o razones (Gan 2011). Los datos nominales, también llamados datos categóricos, son datos discretos sin un orden natural. Los datos ordinales son datos discretos con un orden natural. Los datos intervalares son datos continuos con un orden específico e intervalos iguales. Los datos de razones son datos intervalares con un cero natural.

Existen varias fuentes de datos. En primer lugar, pueden obtenerse datos de investigadores universitarios que recolectan datos primarios. En segundo lugar, los datos pueden obtenerse de organizaciones creadas con el fin de divulgar datos secundarios para la comunidad de investigadores en general. En tercer lugar, los datos pueden obtenerse de los institutos de estadística nacionales y regionales que recolectan datos. Finalmente, las empresas tienen datos corporativos que pueden obtenerse con fines de investigación.

Si bien puede ser difícil obtener datos para abordar un problema de investigación específico o responder una pregunta de negocios, es relativamente fácil obtener datos para probar un modelo o un algoritmo para el análisis de datos. En la era moderna, los lectores pueden obtener conjuntos de datos de Internet fácilmente. La siguiente es una lista de algunos sitios web para obtener datos del mundo real:

• UCI Machine Learning Repository Este sitio de la Web (url: http://archive.ics.uci.edu/ml/index.php) mantiene más de 400 conjuntos de datos que se pueden usar para probar algoritmos de aprendizaje de máquina.

• Kaggle El sitio web de Kaggle (url: https://www.kaggle.com/) incluye conjuntos de datos del mundo real utilizados para competencias de ciencia de datos. Los lectores pueden descargar datos de Kaggle registrando una cuenta.

• DrivenData DrivenData tiene como objetivo aportar prácticas de vanguardia en la ciencia de datos para resolver algunos de los mayores desafíos sociales del mundo. En su sitio web (url: https://www.drivendata.org/), los lectores pueden participar en competencias de ciencia de datos y descargar conjuntos de datos.

• Analytics Vidhya Este sitio web (url: https://datahack.analyticsvidhya.com/contest/all/) le permite participar y descargar conjuntos de datos de problemas de práctica y problemas de hackathon.

• KDD Cup La copa KDD es la competencia anual de Minería de Datos y Descubrimiento de Conocimientos organizado por el grupo de interés especial de la ACM sobre Descubrimiento de Conocimientos y Minería de Datos. Este sitio de la Web (url: http://www.kdd.org/kdd-cup) contiene los conjuntos de datos utilizados en competencias anteriores de la Copa KDD desde 1997.

• U.S. Government’s open data Este sitio web (url: https://www.data.gov/) contiene alrededor de 200.000 conjuntos de datos que cubren una amplia gama de áreas incluidos clima, educación, energía y finanzas.

• AWS Public Datasets En este sitio web (url: https://aws.amazon.com/datasets/), Amazon proporciona un repositorio centralizado de conjuntos de datos públicos, incluidos algunos conjuntos de datos enormes.

13.1.2 Estructuras de Datos y Almacenamiento

Como se mencionó en la sección anterior, hay datos estructurados y tambien datos no estructurados. Los datos estructurados son datos altamente organizados y usualmente tienen el siguiente formato tabular:

\[ \begin{matrix} \begin{array}{lllll} \hline & V_1 & V_2 & \cdots & V_d \ \\\hline \textbf{x}_1 & x_{11} & x_{12} & \cdots & x_{1d} \\ \textbf{x}_2 & x_{21} & x_{22} & \cdots & x_{2d} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ \textbf{x}_n & x_{n1} & x_{n2} & \cdots & x_{nd} \\ \hline \end{array} \end{matrix} \]

En otras palabras, los datos estructurados pueden ser organizados en una tabla que consta de filas y columnas. Usualmente, cada fila representa un registro y cada columna representa un atributo. Una tabla puede descomponerse en varias tablas que pueden almacenarse en una base de datos relacional como Microsoft SQL Server. El SQL (Lenguaje de Consulta Estructurado, según sus siglas en inglés) se puede utilizar para acceder y modificar los datos de manera fácil y eficiente.

Los datos no estructurados no siguen un formato regular (Abdullah and Ahmad 2013). Ejemplos de datos no estructurados incluyen documentos, videos y archivos de audio. La mayoría de los datos con los que nos encontramos son datos no estructurados. En efecto, el término “big data” fue acuñado para reflejar este hecho. Las bases de datos relacionales tradicionales no pueden hacer frente a los desafíos que involucran las variedades y escalas introducidas por los datos masivos no estructurados hoy en día. Ninguna base de datos en SQL ha sido utilizada para almacenar datos masivos no estructurados.

Hay tres bases de datos principales NoSQL (Chen et al. 2014): Bases de datos clave-valor, bases de datos orientadas a columnas y bases de datos orientadas a documentos. Las bases de datos clave-valor utilizan un modelo de datos simple y almacenan los datos según los valores clave. Las versiones modernas de bases de datos clave-valor tienen mayor capacidad de expansión y menores tiempos de respuesta a las consultas que las bases de datos relacionales. Ejemplos de este tipo de base de datos incluyen Dynamo que es usada por Amazon y Voldemort usada por LinkedIn. Las bases de datos orientadas a columnas almacenan y procesan datos por columnas en lugar de filas. Las columnas y las filas se segmentan en múltiples nodos para lograr la capacidad de expansión. Ejemplos de bases de datos orientadas a columnas incluyen BigTable desarrollada por Google y Cassandra desarrollada por Facebook. Las bases de datos orientadas a documentos están diseñadas para soportar formas de datos más complejas que las almacenadas en bases de datos clave-valor. Ejemplos de bases de datos documentales incluyen MongoDB, SimpleDB y CouchDB. MongoDB es una base de datos documental de código abierto que almacena documentos como objetos binarios. SimpleDB es una base de datos distribuida NoSQL usada por Amazon. CouchDB es otra base de datos de codigo abierto orientada a documentos.

13.1.3 Calidad de los Datos

La precisión en los datos es esencial para un análisis de datos útil. La falta de datos precisos puede resultar en costos significativos para las organizaciones en cuanto a actividades de corrección, pérdida de clientes, pérdida de oportunidades y decisiones incorrectas (Olson 2003).

Los datos tienen calidad si satisfacen su uso previsto, es decir, cuando son precisos, oportunos, relevantes, completos, entendibles y confiables (Olson 2003). Por lo tanto, para evaluar la calidad de los datos, primero necesitamos conocer las especificaciones de los usos previstos y después juzgar su idoneidad para esos usos. La utilización de datos para propósitos no previstos puede surgir por una variedad de razones y nos lleva a serios problemas.

La precisión es el componente más importante de los datos de alta calidad. Los datos precisos tienen las siguientes propiedades (Olson 2003):

• No hay elementos faltantes y poseen valores válidos.
• Los valores de los elementos están dentro de los rangos correctos y tienen las representaciones correctas.

Los datos imprecisos surgen de diferentes fuentes. En particular, las siguientes áreas son áreas comunes donde ocurren datos inexactos:

• Entrada inicial de datos. Errores (incluyendo errores deliberados) y errores del sistema pueden ocurrir durante la entrada inicial de los datos. Procesos de entrada de datos defectuosos pueden resultar en datos imprecisos.
• Deterioro de los datos, Deterioro de los datos también conocido como degradación de los datos, se refiere a la corrupción gradual de los datos debido a la acumulación de fallas no críticas en el dispositivo de almacenamiento.
• Movimiento y reestructuración de los datos. Datos imprecisos también pueden surgir de la extracción, limpieza, transformación, carga o integración de datos.
• Uso de los datos. Reportes defectuosos y falta de entendimiento pueden dar lugar a datos imprecisos.

La reverificación y el análisis son dos enfoques utilizados para identificar elementos imprecisos en los datos. El primer enfoque se hace manualmente por personas contrastando cada elemento de los datos con su fuente original. El segundo enfoque es hecho por un software con las habilidades de un analista para buscar en los datos y encontrar posibles datos imprecisos. Para asegurar que los elementos de los datos son 100% precisos, debemos utilizar la reverificación. Sin embargo, ésta puede consumir tiempo y puede no ser posible para algunos datos. También se pueden utilizar técnicas analíticas para identificar elementos imprecisos en los datos. Hay cinco tipos de análisis que se pueden hacer para identificar datos imprecisos (Olson 2003): análisis de elementos de los datos, análisis estructural, correlación de valores, correlación de agregación e inspección de valores.

Las empresas pueden establecer un programa de aseguramiento de la calidad de los datos para crear bases de datos de alta calidad. Para más información acerca de la gestión de los problemas de calidad y técnicas de elaboración de perfiles de datos, los lectores se pueden remitir a Olson (2003).

13.1.4 Limpieza de los Datos

Usualmente es necesario limpiar los datos en bruto antes de poder realizar un análisis útil. En particular, hay que prestar atención a las siguientes áreas al preparar los datos para el análisis (Janert 2010):

• Valores faltantes Es común tener valores faltantes en los datos brutos. Dependiendo de la situación, podemos descartar el registro, descartar la variable o imputar los valores faltantes.

• Valores atípicos Los datos brutos pueden contener datos inusuales como los valores atípicos. Necesitamos tratar cuidadosamente los datos atípicos y no podemos solo removerlos sin saber la razón de su existencia. Algunas veces los datos atípicos son causados por errores administrativos. Algunas veces son justamente el efecto que estamos buscando.

• Basura Los datos brutos pueden contener basura como caracteres no reconocibles que son poco frecuentes y no fáciles de detectar. Sin embargo, pueden causar serios problemas en aplicaciones posteriores.

• Formato Los datos brutos pueden estar en un formato que es inconveniente para análisis posteriores. Por ejemplo, los componentes de un registro pueden estar separados en múltiples líneas en un archivo de texto. En tales casos, las líneas correspondientes a un único registro deben combinarse antes de cargarlas en un software de análisis de datos como R.

• Registros duplicados Los datos brutos pueden contener registros duplicados, los cuales deben ser identificados y eliminados. Esta tarea puede no ser tan sencilla dependiendo de lo que se considere como “registro duplicado.”

• Conjuntos de datos combinados Los datos brutos pueden proceder de diferentes fuentes. En tales casos, necesitamos combinar los datos de las diferentes fuentes para asegurar su compatibilidad.

Para más información acerca de cómo manejar datos en R, los lectores se pueden remitir a Forte (2015) y Buttrey and Whitaker (2017).

13.2 Análisis Preliminar de los Datos

El análisis de datos consiste en inspeccionar, limpiar, transformar y modelar los datos para descubrir información útil que permita sacar conclusiones y tomar decisiones. El análisis de datos tiene una larga historia. En 1962, el estadístico John Tukey definió el análisis de datos como:

procedimientos para analizar datos, técnicas para interpretar los resultados de tales procedimientos, maneras de planificar la recolección de datos para facilitar su análisis, hacerlo más preciso o más exacto, y toda la maquinaria y los resultados de la estadística (matemática) que se aplican al análisis de datos.

— (Tukey 1962)

Recientemente, Judd y coautores definieron el análisis de datos por medio de la siguiente ecuación (Judd, McClelland, and Ryan 2017):

\[ \hbox{Datos} = \hbox{Modelo} + \hbox{Error}, \]

Donde Datos representa un conjunto de resultados u observaciones básicas a ser analizadas, Modelo es una representación compacta de los datos y Error es simplemente la cantidad en la que una observación difiere de su representación en el modelo. Usando la ecuación anterior para el análisis de datos, un analista tiene que resolver los siguientes dos objetivos en conflicto:

• incluir más parámetros en el modelo de modo que el modelo represente mejor los datos.
• eliminar parámetros del modelo de modo que el modelo sea simple y parsimonioso.

En esta sección, presentamos una introducción de alto nivel al análisis de datos, incluyendo diferentes tipos de métodos.

13.2.1 Proceso de Análisis de Datos

El análisis de datos es parte de un estudio general. Por ejemplo, la figura 13.1 muestra el proceso de un estudio típico en ciencias sociales y del comportamiento, como se describe en Albers (2017). El análisis de datos consiste de los siguientes pasos:

• Análisis exploratorio El propósito de este paso es tener una idea de las relaciones entre los datos y determinar qué tipo de análisis tiene sentido.

• Análisis estadístico Este paso realiza el análisis estadístico tal como determinar su significancia estadística y el tamaño del impacto.

• Dar sentido a los resultados Este paso interpreta los resultados estadísticos en el contexto del estudio global.

• Determinar las implicaciones Este paso interpreta los datos conectándolos con los objetivos del estudio y con el campo de estudio al que pertenece.

El objetivo del análisis de datos como se describió anteriormente se enfoca en la explicación de algún fenómeno (Ver sección 13.2.5).

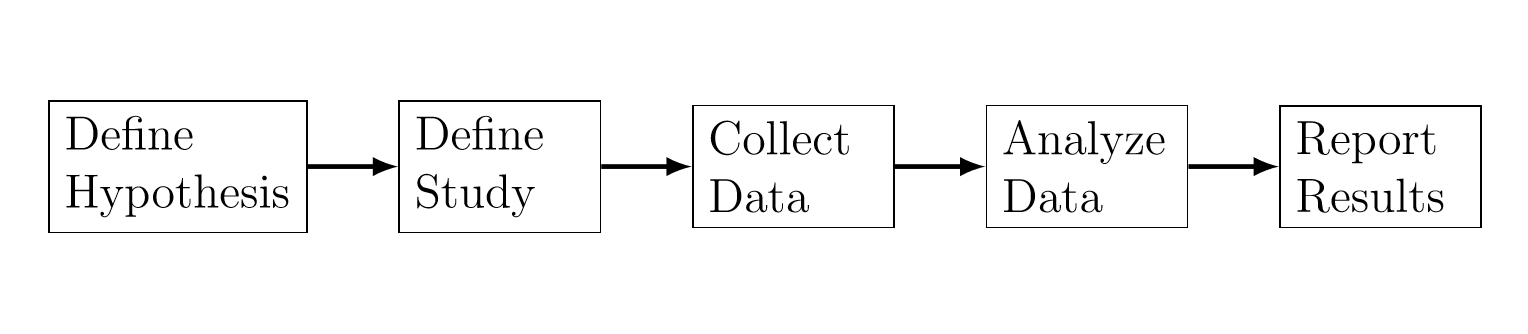
Figure 13.1: El proceso de un estudio típico en ciencias sociales y del comportamiento.

Shmueli (2010) describió un proceso general para la modelación estadística que se muestra en la Figura 13.2. Dependiendo del objetivo del análisis, los pasos difirieren en cuanto a la escogencia del método, los criterios, los datos y la información.

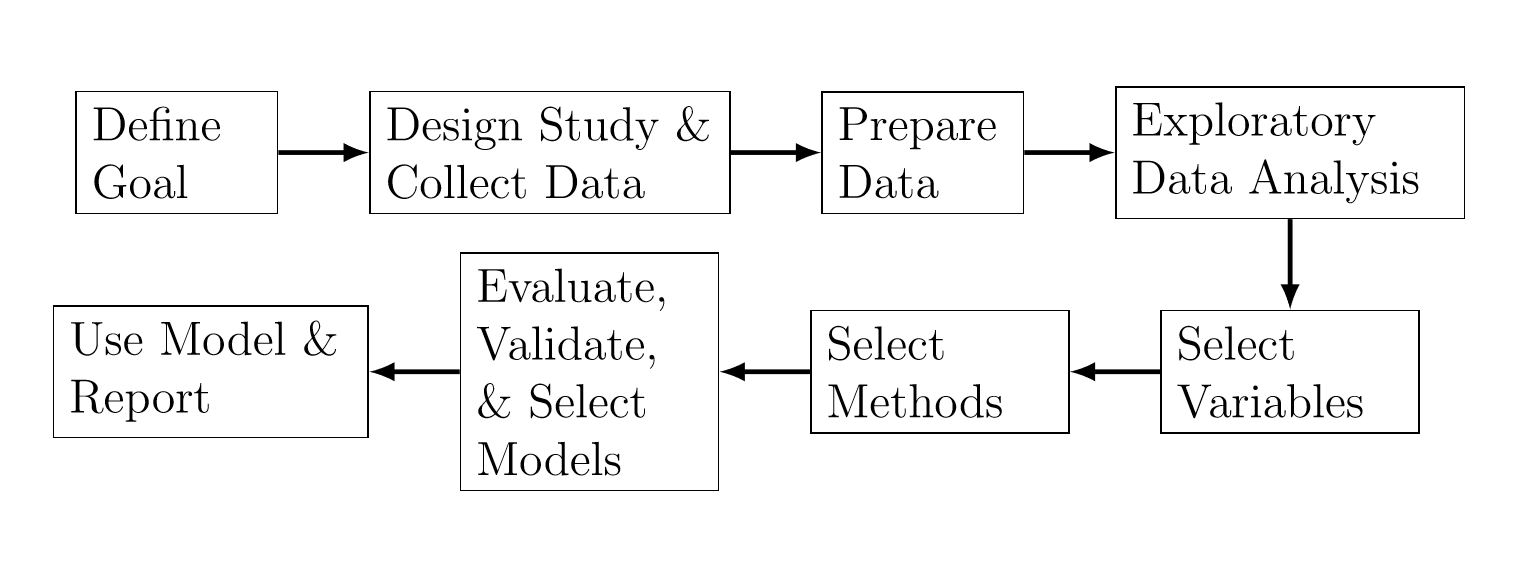
Figure 13.2: El proceso de modelación estadística.

13.2.2 Exploratorio versus Confirmatorio

Existen dos fases del análisis de datos (Good 1983): el Análisis Exploratorio de Datos (EDA, según sus siglas en inglés) y el Análisis Confirmatorio de Datos (CDA,según sus siglas en inglés). La tabla Table 13.1 resume algunas de las diferencias entre EDA y CDA. El EDA se aplica usualmente a datos observables con el objetivo de buscar patrones y formular hipótesis. En contraste, el CDA frecuentemente se aplica a datos experimentales (por ejemplo los datos obtenidos mediante un diseño formal de experimentos) con el objetivo de cuantificar hasta qué punto se espera que las discrepancias entre el modelo y los datos ocurran por azar (Gelman 2004).

\[ \begin{matrix} \begin{array}{lll} \hline & \textbf{EDA} & \textbf{CDA} \\\hline \text{Datos} & \text{Datos observables} & \text{Datos experimentales}\\[3mm] \text{Objetivo} & \text{Reconocimiento de patrones,} & \text{Pruebas de hipótesis,} \\ & \text{formulación de hipótesis} & \text{estimación, predicción} \\[3mm] \text{Técnicas} & \text{Estadística descriptiva, } & \text{Herramientas estadísticas tradicionales de } \\ & \text{visualización, análisis de conglomerados} & \text{inferencia, significancia y confianza}\\ & & \text{} \\ \hline \end{array} \end{matrix} \] Table 13.1: Comparación entre el análisis exploratorio de datos y el análisis confirmatorio de datos.

Las técnicas para el EDA incluyen estadísticas descriptivas (media, mediana, desviación estándar, cuantiles), distribuciones, histogramas, análisis de correlación, reducción de la dimensión y análisis de conglomerados. Las técnicas para el CDA incluyen las herramientas estadísticas tradicionales de inferencia, significancia y confianza.

13.2.3 Supervisado versus No Supervisado

Los métodos para el análisis de datos se pueden dividir en dos categorías (Abbott 2014; Igual and Segu 2017): métodos de aprendizaje supervisado y métodos de aprendizaje no supervisado. Los métodos de aprendizaje supervisado trabajan con datos etiquetados que incluyen una variable objetivo. Matemáticamente, los métodos de aprendizaje supervisado intentan aproximar la siguiente función:

\[ Y = f(X_1, X_2, \ldots, X_p), \]

donde \(Y\) es una variable objetivo y \(X_1\), \(X_2\), \(\ldots\), \(X_p\) son variables explicativas. También se usan otros términos para referirse a la variable objetivo. La tabla Table 13.2 muestra una lista de nombres comunes para los diferentes tipos de variables (Edward W. Frees 2009c). Cuando la variable objetivo es una variable categórica, los métodos de aprendizaje supervisado se denominan métodos de clasificación. Cuando la variable objetivo es continua, los métodos de aprendizaje supervisado se denominan métodos de regresión.

\[ \begin{matrix} \begin{array}{ll} \hline \textbf{Variable objetivo} & \textbf{Variable explicativa}\\\hline \text{Variable dependiente} & \text{Variable independiente}\\ \text{Respuesta} & \text{Tratamiento} \\ \text{Salida} & \text{Entrada} \\ \text{Variable endógena} & \text{Variable exógena} \\ \text{Variable predecida} & \text{Variable predictora} \\ \text{Regresada } & \text{Regresora} \\ \hline \end{array} \end{matrix} \] Table 13.2: Nombres comunes para las diferentes variables.

Los métodos de aprendizaje no supervisado trabajan con datos no etiquetados, que incluyen únicamente variables explicativas. En otras palabras, los métodos de aprendizaje no supervisado no utilizan variables objetivo. Como resultado, los métodos de aprendizaje no supervisados también se denominan métodos de modelación descriptiva.

13.2.4 Paramétricos versus No Paramétricos

Los métodos para análisis de datos pueden ser paramétricos o no paramétricos (Abbott 2014). Los métodos paramétricos asumen que los datos siguen una distribución determinada. Los métodos no paramétricos no asumen distribuciones para los datos y por lo tanto se denominan métodos independientes de la distribución.

Los métodos paramétricos tienen la ventaja de que si la distribución de los datos es conocida, se pueden deducir propiedades tanto de los datos como del método (por ejemplo errores, convergencia, coeficientes). Una desventaja de los métodos paramétricos es que los analistas deben emplear un tiempo considerable buscando la distribución. Por ejemplo, pueden probar diferentes métodos de transformación para transformar los datos de tal forma que sigan una distribución conocida.

Como los métodos no paramétricos hacen menos suposiciones, tienen la ventaja de ser más flexibles, más robustos y aplicables a datos no cuantitativos. Sin embargo, una desventaja de los métodos no paramétricos es que las conclusiones que se derivan no son tan potentes como aquellas que se derivan de los métodos paramétricos.

13.2.5 Explicación versus Predicción

Existen dos objetivos en el análisis de datos (Breiman 2001; Shmueli 2010): explicación y predicción. En algunas áreas científicas como economía, psicología y ciencias ambientales, el análisis de datos se enfoca en explicar las relaciones causales entre las variables de entrada y la variable de respuesta. En otras áreas científicas como el procesamiento de lenguajes naturales y la bioinformática, el enfoque del análisis de datos es predecir las respuestas, dadas las variables de entrada.

Shmueli (2010) expuso en detalle la diferencia entre modelación explicativa y modelación predictiva, la cual refleja el proceso de usar datos y métodos para explicar o predecir. La modelación explicativa se usa comúnmente para construir y comprobar teorías. Sin embargo, la modelación predictiva raramente se usa en campos científicos como herramienta para el desarrollo de teorías.

Una modelación explicativa se hace típicamente como sigue:

• Establecer la teoría predominante.

• Establecer hipótesis causales, las cuales se dan en términos de constructos teóricos más que en variables medibles. Un diagrama causal se incluye usualmente para ilustrar las relaciones hipotéticas de causa entre los constructos teóricos.

• Operar constructos. En este paso, la literatura previa y la justificación teórica se usan para construir un puente entre los constructos teóricos y las mediciones observables.

• Recoger datos y construir modelos junto con las hipótesis estadísticas, que son operadas a partir de las hipótesis de investigación.

• Lograr conclusiones de la investigación y recomendar políticas. Las conclusiones estadísticas se convierten en conclusiones de la investigación. A menudo se acompañan con recomendaciones de políticas.

Shmueli (2010) definió la modelación predictiva como el proceso de aplicar un modelo estadístico o un algoritmo de minería de datos con el propósito de predecir nuevas o futuras observaciones. Estas predicciones incluyen predicciones puntuales, predicciones por intervalos, regiones, distribuciones y clasificaciones de nuevas observaciones. Un modelo predictivo puede ser cualquier método que produce predicciones.

13.2.6 Modelación de Datos versus Modelación Algorítmica

Breiman (2001) presentó dos culturas en el uso de la modelación estadística para extraer conclusiones de los datos: la cultura de la modelación de datos y la cultura de la modelación algorítmica. En la cultura de la modelación de datos, se asume que los datos son generados por un modelo estocástico dado. En la cultura de la modelación algorítmica, el comportamiento de los datos se trata como desconocido y se utilizan modelos algorítmicos.

La modelación de datos le permite al área estadística muchos logros en el análisis de datos y en adquirir información sobre su comportamiento. Sin embargo, Breiman (2001) argumentaba que el enfoque en la modelación de datos por parte de la comunidad estadística ha provocado algunos efectos secundarios tales como:

• Produjo teorías irrelevantes y conclusiones científicas cuestionables.

• Evitó que los estadísticos utilizaran modelos algorítmicos que podrían haber sido más apropiados.

• Restringió la habilidad de los estadísticos para manejar un amplio rango de problemas.

La modelación algorítmica fue usada por los estadísticos industriales hace mucho tiempo. Sin embargo, el desarrollo de los métodos algorítmicos fue asumido por una comunidad externa a la estadística (Breiman 2001). El objetivo de la modelación algorítmica es la precisión predictiva. Para algunos problemas complejos de predicción, los modelos de datos no son apropiados. Estos problemas de predicción incluyen reconocimiento de voz, reconocimiento de imágenes, reconocimiento de texto caligráfico, predicción de series de tiempo no lineales y predicción del mercado financiero. La teoría en la modelación algorítmica se enfoca en las propiedades de los algoritmos, tales como la convergencia y la precisión predictiva.

13.2.7 Análisis de Grandes Volúmenes de Datos (Big Data)

A diferencia del análisis de datos tradicional, el análisis de grandes volúmenes de datos emplea métodos y herramientas adicionales que pueden extraer rápidamente información de datos masivos. En particular, el análisis de grandes volúmenes de datos utiliza los siguientes métodos de procesamiento (Chen et al. 2014):

• filtro de Bloom Un filtro de Bloom es una estructura de datos probabilística espacio-eficiente que es utilizada para determinar si un elemento pertenece a un conjunto. Tiene las ventajas de alta espacio-eficiencia y alta velocidad de consulta. Una desventaja de usar un filtro de Bloom es que hay cierta tasa de error de reconocimiento.

• Hashing Hashing es un método que transforma los datos en valores numéricos de longitud fija mediante una función hash. Tiene la ventaja de rápida lectura y escritura, sin embargo, es difícil encontrar funciones hash que sean robustas.

• Indexación La Indexación hace referencia a un proceso de particionar datos con el fin de acelerar su lectura. El hashing es un caso particular de indexación.

• Tries Un Trie, también llamado árbol digital, es un método para mejorar la eficiencia de búsqueda por medio de prefijos comunes de cadenas de caracteres para reducir en la mayor medida las comparaciones entre cadenas de caracteres.

• Computación Paralela La Computación Paralela utiliza múltiples recursos computacionales para completar una tarea de cómputo. Las herramientas de computación paralela incluyen la Interfaz de Paso de Mensajes (MPI, según sus siglas en inglés), MapReduce y Dryad.

El análisis de grandes volúmenes de datos se puede llevar a cabo en los siguientes niveles (Chen et al. 2014): nivel de memoria, nivel de inteligencia de negocios (BI, según sus siglas en inglés) y nivel masivo. El análisis a nivel de memoria se realiza cuando los datos se pueden cargar en la memoria de un grupo de computadores. El hardware actual puede manejar cientos de gigabytes (GB) de datos en la memoria. El análisis a nivel de BI puede realizarse cuando los datos superan el nivel de memoria. Es usual que los productos de análisis de nivel BI soporten datos del orden de terabytes (TB). El análisis de nivel masivo se lleva a cabo cuando los datos superan las capacidades de los productos para el análisis de nivel BI, normalmente se utilizan Hadoop y MapReduce en el análisis a nivel masivo.

13.2.8 Análisis Reproducibles

Como se mencionó en la sección 13.2.1, un flujo de trabajo típico de análisis de datos incluye recolección de datos, análisis de datos e informe de resultados. Los datos recolectados son grabados en una base de datos o en archivos. Los datos luego son analizados por una o más secuencias de comandos, que pueden grabar algunos resultados intermedios o trabajar siempre sobre los datos en bruto. Finalmente, se elabora un reporte para describir los resultados, que incluye gráficos, tablas y resúmenes de datos relevantes. El flujo de trabajo puede estar sujeto a los siguientes problemas potenciales (Mailund 2017, Capítulo 2):

• Los datos están separados de las secuencias de comandos del análisis.

• La documentación del análisis está separada del propio análisis.

Si el análisis se realiza sobre los datos en bruto con una única secuencia de comandos, entonces el primer punto no es un problema importante. Si el análisis consiste en múltiples secuencias de comandos y una secuencia de comando graba resultados intermedios que son leídos por la siguiente secuencia de comandos, entonces las secuencias de comandos describen un flujo de trabajo de análisis de datos. Para reproducir un análisis, las secuencias de comandos deben ejecutarse en el orden correcto. El flujo de trabajo puede causar grandes problemas si el orden de las secuencias de comandos no está documentado o la documentación no está actualizada o se pierde. Una forma de resolver el primer problema es escribir las secuencias de comandos de forma que cualquier parte del flujo de trabajo se pueda ejecutar de forma completamente automática en cualquier momento.

Si la documentación del análisis está sincronizada con el análisis, entonces la segunda cuestión no es un gran problema. Sin embargo, la documentación puede resultar inútil si las secuencias de comandos se modifican, pero la documentación no se actualiza.

La programación literaria es un enfoque para abordar los dos problemas mencionados anteriormente. En la programación literaria, la documentación de un programa y el código del programa se escriben juntos. Una forma para hacer programación literaria en R, es usar R Markdown y el paquete \(\texttt{knitr}\).

13.2.9 Problemas Éticos

Los analistas pueden enfrentarse a problemas y dilemas éticos durante el proceso de análisis de datos. En algunos campos, por ejemplo, los problemas y dilemas éticos incluyen el consentimiento de los participantes, los beneficios, el riesgo, la confidencialidad y la propiedad de los datos (Miles, Hberman, and Sdana 2014). Para el análisis de datos en las ciencias actuariales y en los seguros en particular, nos enfrentamos a las siguientes cuestiones y problemas éticos (Miles, Hberman, and Sdana 2014):

• Lo valioso del proyecto ¿Vale la pena realizar el proyecto? ¿Contribuirá el proyecto de forma significativa a un ámbito más amplio que mi carrera? Si un proyecto es sólo oportunista y no tiene una importancia mayor, puede que se lleve a cabo con menos cuidado. El resultado puede parecer bueno, pero no ser el adecuado.

• Competencia ¿Tengo o todo el equipo tiene la habilidad para llevar a cabo el proyecto? La incompetencia puede llevar a debilidades en el análisis, como recolectar grandes cantidades de datos de forma deficiente y extraer conclusiones superficiales.

• Beneficios, costos y reciprocidad ¿Cada una de las partes interesadas se beneficiará del proyecto? ¿Son equitativos los beneficios y los costos? Un proyecto probablemente fracasará si el beneficio y el costo para una parte interesada no se armonizan.

• Privacidad y confidencialidad ¿Cómo nos aseguramos de que la información se mantenga de forma confidencial? Dónde se almacenan los datos en bruto y los resultados de los análisis y cómo tener acceso a ellos debe ser documentado en acuerdos de confidencialidad explícitos.

13.3 Técnicas de Análisis de Datos

Las técnicas para análisis de datos provienen de campos diferentes pero interrelacionados como la estadística, el aprendizaje de máquina, el reconocimiento de patrones y la minería de datos. La estadística es un campo que aborda formas confiables de recolectar datos y hacer inferencias basados en ellos (Bandyopadhyay and Forster 2011; Bluman 2012). El término aprendizaje de máquina fue acuñado por Samuel en 1959 (Samuel 1959). Originalmente aprendizaje de máquina se refiere al campo de estudio en el cual los computadores son capaces de aprender sin ser programados explícitamente. Hoy en dia, el aprendizaje de máquina ha evolucionado al amplio campo de estudio en el que los métodos de computación utilizan la experiencia (es decir la información pasada disponible para el análisis) para mejorar el desempeño o para hacer predicciones precisas (C. M. Bishop 2007; Clarke, Fokoue, and Zhang 2009; Mohri, Rostamizadeh, and Talwalkar 2012; Kubat 2017). Hay cuatro tipos de algoritmos de aprendizaje de máquina (Ver Table 13.3) dependiendo del tipo de datos y el tipo de tareas de aprendizaje.

\[ \begin{matrix} \begin{array}{rll} \hline & \textbf{Supervisado} & \textbf{No supervisado} \\\hline \textbf{Datos discretos} & \text{Clasificación} & \text{Conglomerados} \\ \textbf{Datos continuos} & \text{Regresión} & \text{Reducción de dimensión} \\ \hline \end{array} \end{matrix} \] Table 13.3: Tipos de algoritmos de aprendizaje de máquina.

Teniendo su origen en la ingeniería, el reconocimiento de patrones es un campo estrechamente relacionado con el aprendizaje de máquina, el cual surgió de la informática. De hecho, el reconocimiento de patrones y el aprendizaje de máquina pueden ser considerados como dos facetas del mismo campo (C. M. Bishop 2007). La minería de datos es un campo que se ocupa de recopilar, limpiar, procesar, analizar y obtener conclusiones útiles de los datos (Aggarwal 2015).

13.3.1 Técnicas exploratorias

Las técnicas de análisis exploratorio de datos incluyen la estadística descriptiva, así como muchas técnicas de aprendizaje no supervisado tales como el análisis de conglomerados y el análisis de componentes principales.

13.3.1.1 Estadísticas descriptivas

En el sentido indefinido, la estadística descriptiva es un área de la estadística que se ocupa de la recolección, organización, resumen y presentación de datos (Bluman 2012). En el sentido definido, las estadísticas descriptivas son estadísticas de resumen que describen cuantitativamente o resumen los datos.

\[ \begin{matrix} \begin{array}{ll} \hline & \textbf{Estadísticas descriptivas} \\\hline \text{Medidas de tendencia central} & \text{Media, mediana, moda, rango medio}\\ \text{Medidas de variación} & \text{Rango, varianza, desviación estándar} \\ \text{Medidas de posición} & \text{Cuantiles} \\ \hline \end{array} \end{matrix} \] Table 13.4: Algunas estadísticas descriptivas comúnmente utilizadas.

La tabla 13.4 muestra algunas estadísticas descriptivas comúnmente usadas. En R podemos usar la función \(\texttt{summary}\) para calcular algunas de las estadísticas descriptivas. Para datos numéricos podemos visualizar las estadísticas descriptivas utilizando un diagrama de caja (boxplot).

Además de esas estadísticas descriptivas cuantitativas, también podemos describir cualitativamente la forma de las distribuciones (Bluman 2012). Por ejemplo, podemos decir que una distribución es sesgada positivamente, simétrica o sesgada negativamente. Para visualizar la distribución de una variable podemos graficar un histograma.

13.3.1.2 Análisis de componentes principales

El análisis de componentes principales (PCA, según sus siglas en inglés) es un procedimiento estadístico que transforma un conjunto de datos descrito por variables posiblemente correlacionadas en un conjunto descrito por variables linealmente no correlacionadas, las cuales son llamadas componentes principales y están ordenadas de acuerdo con sus varianzas. El PCA es una técnica para la reducción de la dimensionalidad. Si las variables originales están altamente correlacionadas, entonces las primeras componentes principales pueden explicar la mayor parte de la variación de los datos originales.

Las componentes principales de las variables están relacionadas con valores propios y vectores propios de la matriz de covarianza de las variables. Para \(i=1,2,\ldots,d\), sea \((\lambda_i, \textbf{e}_i)\) el \(i\)-ésimo par de valor propio - vector propio de la matriz de covarianzas \({\Sigma}\) de \(d\) variables \(X_1,X_2,\ldots,X_d\) tal que \(\lambda_1\ge \lambda_2\ge \ldots\ge \lambda_d\ge 0\) y los vectores propios están normalizados. Entonces la \(i\)-ésima componente principal está dada por

\[ Z_{i} = \textbf{e}_i' \textbf{X} =\sum_{j=1}^d e_{ij} X_j, \]

donde \(\textbf{X}=(X_1,X_2,\ldots,X_d)'\). Se puede mostrar que \(\mathrm{Var~}{(Z_i)} = \lambda_i\). Como resultado, la proporción de la varianza explicada por la \(i\)-ésima componente principal se calcula como,

\[ \dfrac{\mathrm{Var~}{(Z_i)}}{ \sum_{j=1}^{d} \mathrm{Var~}{(Z_j)}} = \dfrac{\lambda_i}{\lambda_1+\lambda_2+\cdots+\lambda_d}. \]

Para más información sobre PCA, los lectores se pueden remitir a Mirkin (2011).

13.3.1.3 Análisis de Conglomerados

El análisis de conglomerados (también llamado análisis cluster) se refiere al proceso de dividir un conjunto de datos en agrupaciones homogéneas o conglomerados de modo que puntos en el mismo grupo sean similares y puntos de diferentes grupos sean bastante distintos (Gan, Ma, and Wu 2007; Gan 2011). La agrupación de datos es una de las herramientas más populares para el análisis exploratorio de datos y ha tenido aplicaciones en muchos áreas científicas.

Durante las últimas décadas, se han propuesto varios tipos de algoritmos de agrupación, dentro de los cuales el algoritmo de k-medias es tal vez el más conocido debido a su simplicidad. Para describir el algoritmo de k-medias, sea \(X=\{\textbf{x}_1,\textbf{x}_2,\ldots,\textbf{x}_n\}\) un conjunto de datos que contiene \(n\) puntos, cada uno de los cuales es descrito por \(d\) características numéricas. Dado un número determinado de agrupaciones \(k\), el algoritmo de \(k\)-medias apunta a minimizar la siguiente función objetivo:

\[ P(U,Z) = \sum_{l=1}^k\sum_{i=1}^n u_{il} \Vert \textbf{x}_i-\textbf{z}_l\Vert^2, \]

donde \(U=(u_{il})_{n\times k}\) es una matriz de partición \(n\times k\), \(Z=\{\textbf{z}_1,\textbf{z}_2,\ldots,\textbf{z}_k\}\) es un conjunto de centros de los grupos, y, \(\Vert\cdot\Vert\) es la norma \(L^2\) o distancia euclidiana. La matriz de partición \(U\) satisface las siguientes condiciones:

\[ u_{il}\in \{0,1\},\quad i=1,2,\ldots,n,\:l=1,2,\ldots,k, \]

\[ \sum_{l=1}^k u_{il}=1,\quad i=1,2,\ldots,n. \] El algoritmo de \(k\)-medias emplea un procedimiento iterativo para minimizar la función objetivo, el cual actualiza repetidamente la matriz de partición \(U\) y los centros de los grupos \(Z\) secuencialmente hasta que cumpla algún criterio para detenerse. Para más información acerca de \(k\)-medias, los lectores se pueden remitir a Gan, Ma, and Wu (2007) y Mirkin (2011).

13.3.2 Técnicas confirmatorias

Las técnicas confirmatorias de análisis de datos incluyen las herramientas estadísticas tradicionales de inferencia, significancia y confianza.

13.3.2.1 Modelos lineales

Los modelos lineales, también llamados modelos de regresión lineal, apuntan a utilizar una función lineal para aproximar la relación entre la variable dependiente y las variables independientes. Un modelo de regresión lineal es llamado un modelo de regresión lineal simple si tiene únicamente una variable independiente. Cuando hay más de una variable independiente involucrada, se llama modelo de regresión lineal múltiple.

Sean \(X\) y \(Y\) que denotan las variables independiente y dependiente respectivamente. Para \(i=1,2,\ldots,n\), sean \((x_i, y_i)\) los valores observados de \((X,Y)\) en el \(i\)-ésimo caso. Entonces el modelo de regresión lineal simple se especifica como sigue (Edward W. Frees 2009c):

\[ y_i = \beta_0 + \beta_1 x_i + \epsilon_i,\quad i=1,2,\ldots,n, \]

donde \(\beta_0\) y \(\beta_1\) son parámetros y \(\epsilon_i\) es una variable aleatoria que representa el error para el \(i\)-ésimo caso.

Cuando hya múltiples variables independientes, se usa el siguiente modelo de regresión lineal múltiple:

\[ y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik} + \epsilon_i, \]

donde \(\beta_0\), \(\beta_1\), \(\ldots\), \(\beta_k\) son parámetros desconocidos a estimar.

Los modelos de regresión lineal usualmente asumen los siguientes supuestos:

1. \(x_{i1},x_{i2},\ldots,x_{ik}\) son variables no estocásticas.

2. \(\mathrm{Var~}(y_i)=\sigma^2\), donde \(\mathrm{Var~}(y_i)\) denota la varianza de \(y_i\).

3. \(y_1,y_2,\ldots,y_n\) son variables aleatorias independientes.

Con el propósito de obtener pruebas y declaraciones de confianza con muestras pequeñas, también se hace el siguiente supuesto de normalidad fuerte:

4. \(\epsilon_1,\epsilon_2,\ldots,\epsilon_n\) son normalmente distribuidas.

13.3.2.2 Modelos lineales generalizados

El modelo lineal generalizado (GLM, según sus siglas en inglés) es una amplia familia de modelos de regresión que incluye modelos de regresión lineal como casos particulares. En un GLM, se asume que la media de la respuesta (es decir, la variable dependiente) es una función de combinaciones lineales de las variables explicativas, es decir,

\[ \mu_i = E[y_i], \]

\[ \eta_i = \textbf{x}_i'\boldsymbol{\beta} = g(\mu_i), \]

donde \(\textbf{x}_i=(1,x_{i1}, x_{i2}, \ldots, x_{ik})'\) es un vector de valores del regresor, \(\mu_i\) es la respuesta media para el \(i\)-ésimo caso, y \(\eta_i\) es un componente sistemático del GLM. La función \(g(\cdot)\) es conocida y es llamada la función de enlace. La respuesta media puede variar en función de las observaciones permitiendo que algunos parámetros cambien. Sin embargo, se asume que los parámetros de regresión \(\boldsymbol{\beta}\) son los mismos entre las diferentes observaciones.

Los GLMs hacen los siguientes supuestos:

1. \(x_{i1},x_{i2},\ldots,x_{in}\) son variables no estocásticas.

2. \(y_1,y_2,\ldots,y_n\) son independientes.

3. Se asume que la variable dependiente sigue una distribución de la familia exponencial lineal.

4. La varianza de la variable dependiente no se asume constante, pero es una función de la media, es decir,

\[ \mathrm{Var~}{(y_i)} = \phi \nu(\mu_i), \]

donde \(\phi\) es el parámetro de dispersión y \(\nu(\cdot)\) es una función.

Como podemos ver en la especificación anterior, el GLM proporciona un marco unificador para manejar diferentes tipos de variables dependientes, incluyendo variables discretas y continuas. Para más información acerca de los GLMs, los lectores se pueden remitir a Jong and Heller (2008), y Edward W. Frees (2009c).

13.3.2.3 Modelos basados en árboles

Los árboles de decisión también conocidos como modelos basados en árboles, implican la división del espacio predictor (es decir, el espacio formado por las variables independientes) en un numero de regiones simples y el uso de la media o la moda de la región para la predicción (Breiman et al. 1984). Hay dos tipos de modelos basados en árboles: árboles de clasificación y árboles de regresión. Cuando la variable dependiente es categórica, los modelos de árbol resultantes se llaman árboles de clasificación. Cuando la variable dependiente es continua, los modelos de árbol resultantes se denominan árboles de regresión.

El proceso de construcción de árboles de clasificación es similar al de construcción de árboles de regresión. Aquí solo describimos brevemente cómo construir un árbol de regresión. Para hacerlo, el espacio predictor se divide en regiones no solapadas que minimizan la siguiente función objetivo

\[ f(R_1,R_2,\ldots,R_J) = \sum_{j=1}^J \sum_{i=1}^n I_{R_j}(\textbf{x}_i)(y_i - \mu_j)^2 \]

donde \(I\) es una función indicadora, \(R_j\) denota el conjunto de índices de las observaciones que pertenecen a la \(j\)-ésima región, \(\mu_j\) es la respuesta media de las observaciones en la \(j\)-ésima región, \(\textbf{x}_i\) es el vector de los valores predictores para la \(i\)-ésima observación, y \(y_i\) es el valor respuesta para la \(i\)-ésima observación.

En términos de precisión predictiva, los árboles de decisión generalmente no se desempeñan al nivel de otros modelos de regresión y clasificación. Sin embargo, los modelos basados en árboles pueden superar a los modelos lineales cuando la relación entre la respuesta y los predictores es no lineal. Para más información acerca de árboles de decisión, los lectores se pueden remitir a Breiman et al. (1984) y Mitchell (1997).

13.4 Algunas funciones de R

R es un software de código abierto para computación estadística y gráficos, el cual puede descargarse del sitio web del proyecto R en . En esta sección daremos algunas funciones de R para el análisis de datos, especialmente para tareas de análisis de datos mencionadas en secciones anteriores.

\[ \begin{matrix} \begin{array}{lll} \hline \text{Tarea de análisis de datos} & \text{Paquete de R} & \text{Función de R} \\\hline \text{Estadísticas Descriptivas} & \texttt{base} & \texttt{summary}\\ \text{Análisis de Componentes Principales} & \texttt{stats} & \texttt{prcomp} \\ \text{Análisis de Conglomerados de Datos} & \texttt{stats} & \texttt{kmeans}, \texttt{hclust} \\ \text{Ajuste de Distribuciones} & \texttt{MASS} & \texttt{fitdistr} \\ \text{Modelos de Regresión Lineal} & \texttt{stats} & \texttt{lm} \\ \text{Modelos Lineales Generalizados} & \texttt{stats} & \texttt{glm} \\ \text{Árboles de Regresión} & \texttt{rpart} & \texttt{rpart} \\ \text{Análisis de Sobrevivencia} & \texttt{survival} & \texttt{survfit} \\ \hline \end{array} \end{matrix} \] Table 13.5: Algunas funciones de R para el análisis de datos.

Table 13.5 muestra algunas funciones de R para diferentes tareas de análisis de datos. Los lectores pueden leer la documentación de R para ejemplos de cómo usar estas funciones. También hay otras funciones de R de otros paquetes para hacer tareas similares, sin embargo, las funciones listadas en esta tabla proporcionan buenos puntos de partida para que los lectores realicen análisis de datos en R. Para analizar grandes conjuntos de datos en R de manera eficiente, los lectores se pueden remitir a Daroczi (2015).

13.5 Resumen

En este capítulo, nosotros dimos una visión general de alto nivel del análisis de datos, introduciendo tipos, estructuras, almacenamiento, fuentes, procesos y técnicas de análisis de datos. En particular, presentamos diferentes aspectos del análisis de datos. Adicionalmente, proporcionamos varios sitios web donde los lectores pueden obtener conjuntos de datos reales para potenciar sus habilidades en análisis de datos. También listamos algunos paquetes y funciones de R que pueden utilizarse para realizar varias tareas de análisis de datos.

13.6 Otros recursos y colaboradores

Contributor

• Guojun Gan, Universidad de Connecticut, es el autor principal de la versión inicial de este capítulo. Email: guojun.gan@uconn.edu para comentarios del capítulo y sugerencias de mejora.
• Los revisores del capítulo incluyen a: Min Ji, Toby White.
• Traducción al español: Armando Zarruk (Universidad Nacional de Colombia)